- Главная
- Математика
- Элементы геометрии на небесной сфере. Лекция 1

Содержание
- 2. Элементы геометрии на небесной сфере Одним из основных направлений, относительно которого определяется положение наблюдаемого небесного светила,
- 3. Элементы геометрии на небесной сфере Большой круг небесной сферы, по которому горизонтальная плоскость, проходящая через глаз
- 4. Элементы геометрии на небесной сфере Линия, параллельная земной оси и проходящая через центр небесной сферы, называется
- 5. Элементы геометрии на небесной сфере Небесный экватор пересекается с истинным горизонтом в точках востока, E ,
- 6. Горизонтальная система координат Основной плоскостью является плоскость истинного горизонта, а началом отсчета - точка юга S.
- 7. Вместо высоты светила в качестве первой горизонтальной координаты часто употребляют зенитное расстояние z - угловое расстояние
- 8. Первая экваториальная система координат Основной плоскостью является плоскость небесного экватора, началом отсчета - точка Q. Координатами
- 9. Реже вместо склонения используется полярное расстояние, p, - это угловое расстояние от светила до полюса. Часовой
- 11. Скачать презентацию
Слайд 2Элементы геометрии на небесной сфере
Одним из основных направлений, относительно которого определяется положение
Элементы геометрии на небесной сфере
Одним из основных направлений, относительно которого определяется положение

Плоскость, перпендикулярная отвесной линии, называется горизонтальной плоскостью.
В каждой точке Земли наблюдатель видит половину сферы, вращающейся с востока на запад вместе с прикрепленными к ней звездами. Это видимое вращение небесной сферы объясняется равномерным вращением Земли вокруг своей оси с запада на восток.
Отвесная линия пересекает небесную сферу в точке зенита, Z и в точке надира, Z'.
Слайд 3Элементы геометрии на небесной сфере
Большой круг небесной сферы, по которому горизонтальная плоскость,
Элементы геометрии на небесной сфере
Большой круг небесной сферы, по которому горизонтальная плоскость,

Большим кругом небесной сферы является круг, проходящий через центр небесной сферы.
Круги, образованные пересечением небесной сферы с плоскостями, не проходящими через ее центр, называются малыми кругами.
Слайд 4Элементы геометрии на небесной сфере
Линия, параллельная земной оси и проходящая через центр
Элементы геометрии на небесной сфере
Линия, параллельная земной оси и проходящая через центр

Ось мира наклонена к плоскости истинного горизонта под углом ϕ .
Большой круг небесной сферы, плоскость которого перпендикулярна оси мира, называется небесным экватором. Небесный экватор делит небесную сферу на две части: северную и южную. Небесный экватор параллелен экватору Земли.
Плоскость, проходящая через отвесную линию и ось мира, пересекает небесную сферу по линии небесного меридиана. Небесный меридиан пересекается с истинным горизонтом в точках N и S. Плоскости этих кругов пересекаются по полуденной линии. Небесный меридиан является проекцией на небесную сферу земного меридиана, на котором находится наблюдатель.
Слайд 5Элементы геометрии на небесной сфере
Небесный экватор пересекается с истинным горизонтом в точках
Элементы геометрии на небесной сфере
Небесный экватор пересекается с истинным горизонтом в точках

Большие круги, плоскости которых проходят через отвесную линию, называются вертикалами. Вертикал, проходящий через точки W и E, называется первым вертикалом.
Большие круги, плоскости которых проходят через ось мира, называются кругами склонения или часовыми кругами.
Малые круги небесной сферы, плоскости которых параллельны небесному экватору, называются небесными или суточными параллелями. Суточными они называются потому, что по ним происходит суточное движение небесных светил. Экватор также является суточной параллелью.
Малый круг небесной сферы, плоскость которого параллельна плоскости горизонта, называется альмукантаратом.
Слайд 6Горизонтальная система координат
Основной плоскостью является плоскость истинного горизонта, а началом отсчета -
Горизонтальная система координат
Основной плоскостью является плоскость истинного горизонта, а началом отсчета -

Высота светила над горизонтом, h, - это угловое расстояние от истинного горизонта, измеряемое по вертикалу светила (аналог широты). Высота светила может изменяться в пределах от -90o до 90o. Отрицательная высота означает, что светило находится под горизонтом. Пример: высота зенита равна 90o.
Слайд 7Вместо высоты светила в качестве первой горизонтальной координаты часто употребляют зенитное расстояние
Вместо высоты светила в качестве первой горизонтальной координаты часто употребляют зенитное расстояние

Зенитное расстояние может изменяться в пределах от 0o до 180o, причем светила с зенитным расстоянием больше 90o лежат ниже горизонта и являются ненаблюдаемыми.
Второй горизонтальной координатой является азимут А - это угловое расстояние от точки юга S до пересечения вертикала светила с горизонтом, отсчитываемое вдоль горизонта по часовой стрелке. Азимут может принимать значения от 0o до 360o и носит еще название астрономического азимута, в отличие от геодезического азимута, отсчитываемого от точки севера N по часовой стрелке.
Горизонтальная система координат
Слайд 8Первая экваториальная система координат
Основной плоскостью является плоскость небесного экватора, началом отсчета -
Первая экваториальная система координат
Основной плоскостью является плоскость небесного экватора, началом отсчета -

Склонение светила δ, - это угловое расстояние от небесного экватора до светила, отсчитываемое по кругу склонения. Склонение изменяется в пределах от -90o до 90o, причем светила с δ>0 находятся к северу от экватора, а с δ<0 - к югу от него.
Слайд 9Реже вместо склонения используется полярное расстояние, p, - это угловое расстояние от
Реже вместо склонения используется полярное расстояние, p, - это угловое расстояние от

Часовой угол, t, - это дуга небесного экватора между небесным меридианом и кругом склонения светила. Отсчитывается от точки Q по часовой стрелке. Изменяется в пределах от 0o до 360o в градусной мере или от 0h до 24h в часовой мере (360o соответствует 24h, 1h - 15o, 1m - 15', 1s - 15").
Координаты звезд в горизонтальной и первой экваториальной системах координат изменяются из-за суточного вращения Земли, так как в них начало отсчета привязано к вращающейся Земле (точка юга S и точка Q лежат на небесном меридиане). Значит, для того, чтобы координаты звезд не изменялись из-за суточного вращения, необходимо выбрать точку отсчета, неподвижную относительно звезд и участвующую в суточном вращении. В качестве такой точки отсчета была выбрана точка весеннего равноденствия, и система координат, в которой звезды не изменяют свои координаты из-за суточного вращения, называется второй экваториальной системой координат.
Первая экваториальная система координат
 Параллельные плоскости
Параллельные плоскости Приёмы умножения на 2
Приёмы умножения на 2 Математика 4 класс
Математика 4 класс Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математика в профессии Застройщик
Математика в профессии Застройщик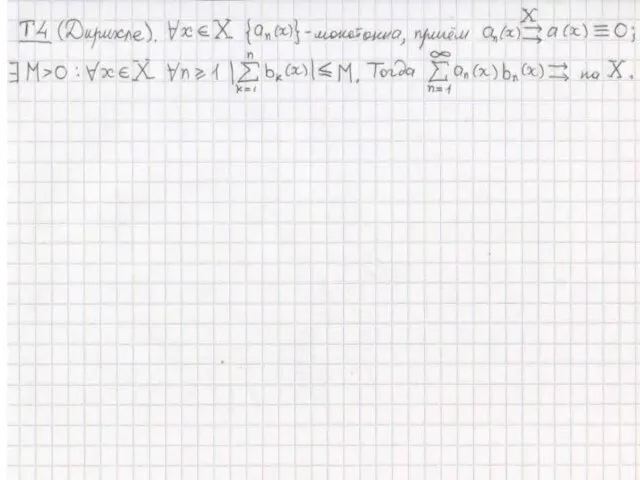 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Пропорции
Презентация на тему Пропорции  Перетворення графіків
Перетворення графіків Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Обыкновенные дроби
Обыкновенные дроби Устная работа. Вычисления
Устная работа. Вычисления Вычисление реакций и перемещений в статически неопределимых системах
Вычисление реакций и перемещений в статически неопределимых системах Перпендикулярные прямые
Перпендикулярные прямые Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Сложение отрицательных чисел
Сложение отрицательных чисел Построение правильных многоугольников
Построение правильных многоугольников Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Золотое сечение. Витрувий
Золотое сечение. Витрувий Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Понятие и виды средних величин
Понятие и виды средних величин Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Логарифм и его свойства
Логарифм и его свойства