Понятие движения. Геометрия 9 класс

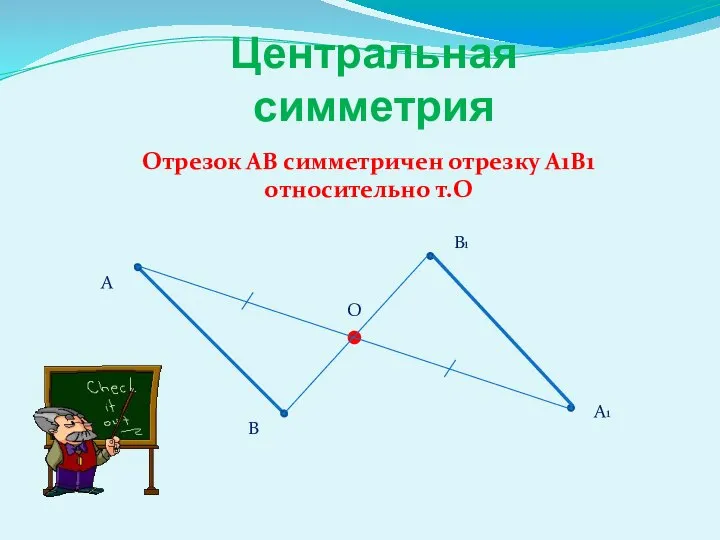
Центральная симметрия
Отрезок АВ симметричен отрезку А1В1 относительно т.О
А
В
О
А1
В1

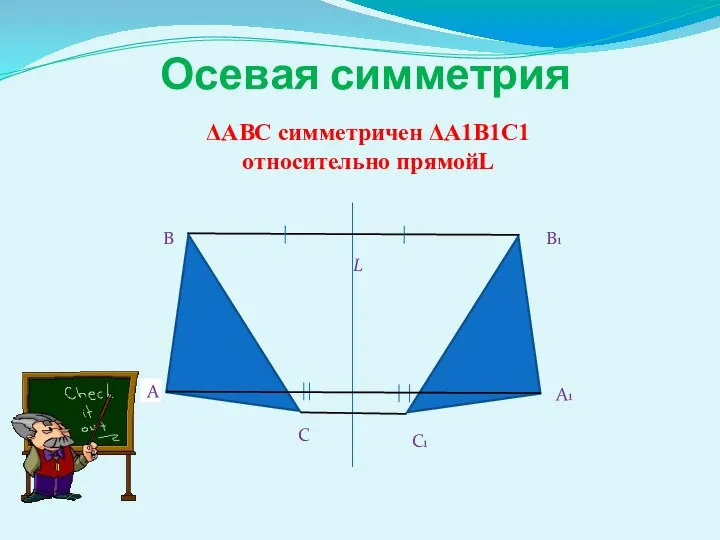
А
В
С
А1
С1
В1
L
Осевая симметрия
ΔАВС симметричен ΔА1В1С1 относительно прямойL

Понятие движения
Пусть каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя.
Осевая симметрия и центральная симметрия есть отображение плоскости на себя.

Понятие движения
В какую фигуру отобразился отрезок АВ при центральной симметрии?
В какую фигуру отобразился треугольник АВС при осевой симметрии?
Сохранилось ли расстояние между точками при осевой симметрии?
При центральной симметрии?

Понятие движения
Определение:
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояние.

Задание № 1
Пусть M и N какие-либо точки, L – ось симметрии. M1 и N1 – точки, симметричные точкам M и N относительно прямой L. Докажите, что расстояние между точками M и N при осевой симметрии сохраняется, т.е.
MN = M1N1.

Задание № 2
Докажите, что центральная симметрия есть движение.

Домашнее задание
п. 113 – п. 114
(до теоремы)
№ 1148 (а)