Объем пирамиды

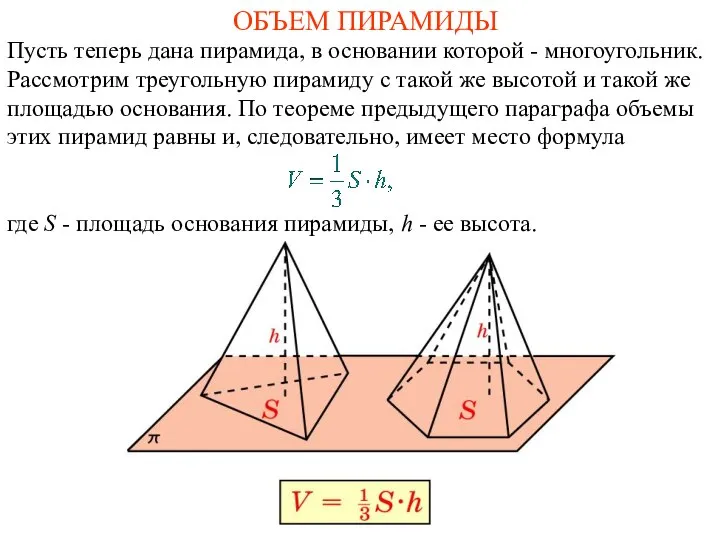
ОБЪЕМ ПИРАМИДЫ
Пусть теперь дана пирамида, в основании которой - многоугольник. Рассмотрим треугольную пирамиду с такой же высотой и такой же площадью основания. По теореме предыдущего параграфа объемы этих пирамид равны и, следовательно, имеет место формула
где S - площадь основания пирамиды, h - ее высота.

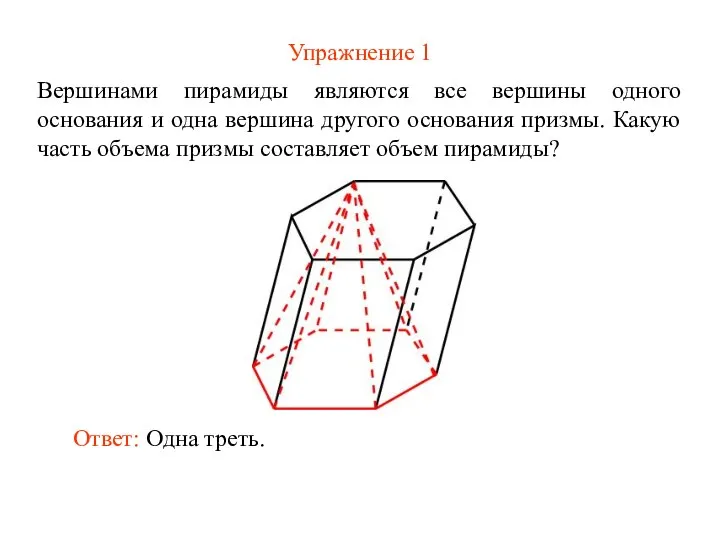
Упражнение 1
Вершинами пирамиды являются все вершины одного основания и одна вершина другого основания призмы. Какую часть объема призмы составляет объем пирамиды?
Ответ: Одна треть.

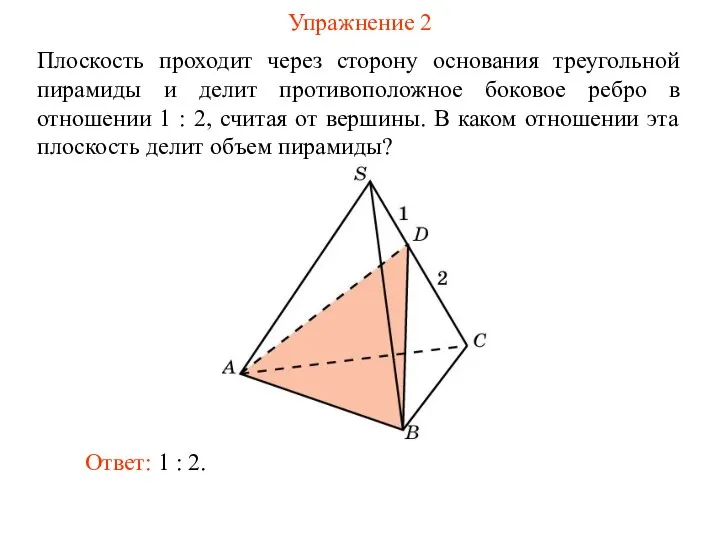
Упражнение 2
Плоскость проходит через сторону основания треугольной пирамиды и делит противоположное боковое ребро в отношении 1 : 2, считая от вершины. В каком отношении эта плоскость делит объем пирамиды?
Ответ: 1 : 2.

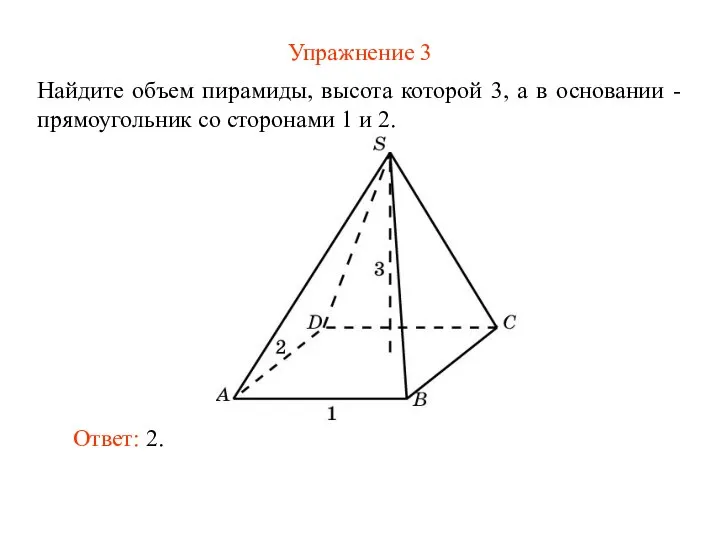
Упражнение 3
Найдите объем пирамиды, высота которой 3, а в основании - прямоугольник со сторонами 1 и 2.
Ответ: 2.

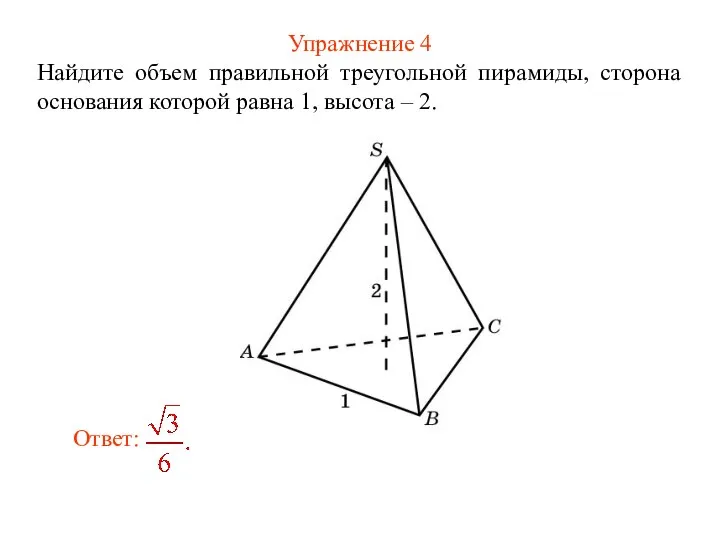
Упражнение 4
Найдите объем правильной треугольной пирамиды, сторона основания которой равна 1, высота – 2.

Упражнение 5
В правильной четырехугольной пирамиде высота 3 м, боковое ребро 5 м. Найдите ее объем.
Ответ: 32 м3.

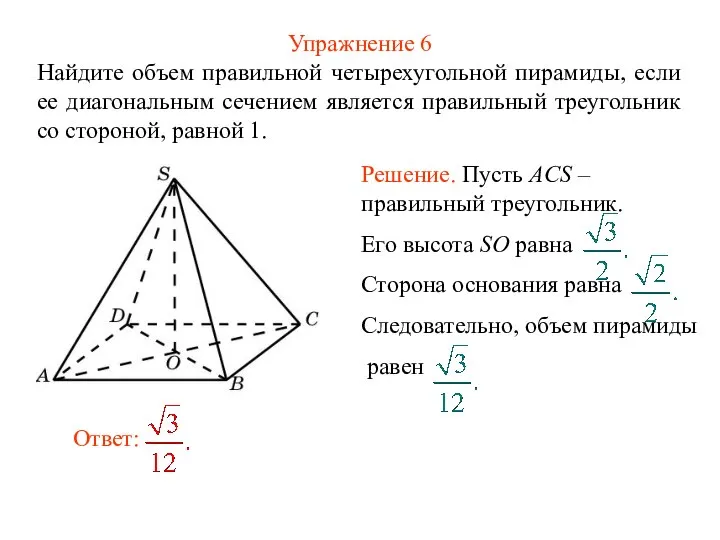
Упражнение 6
Найдите объем правильной четырехугольной пирамиды, если ее диагональным сечением является правильный треугольник со стороной, равной 1.

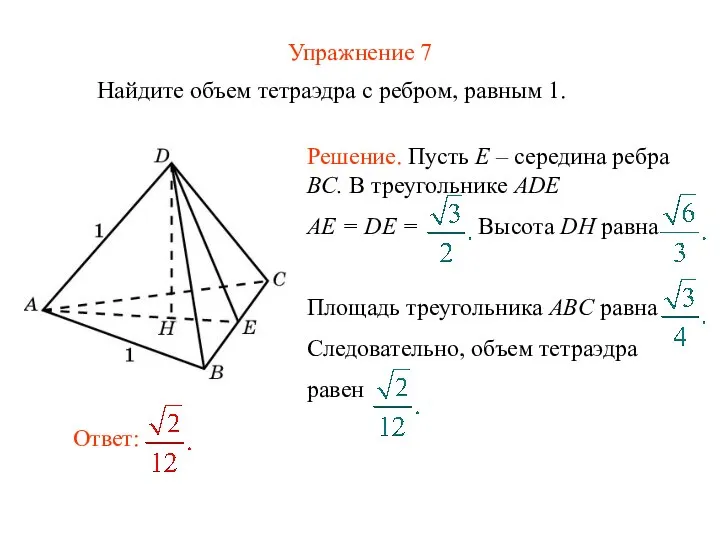
Упражнение 7
Найдите объем тетраэдра с ребром, равным 1.

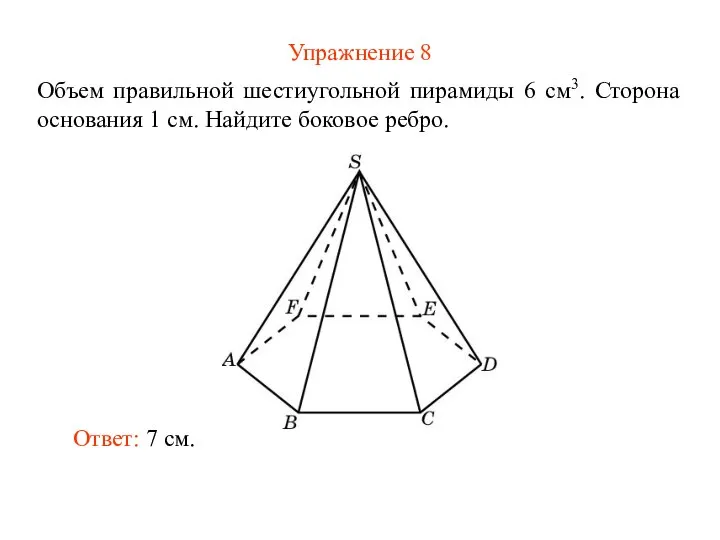
Упражнение 8
Объем правильной шестиугольной пирамиды 6 см3. Сторона основания 1 см. Найдите боковое ребро.
Ответ: 7 см.

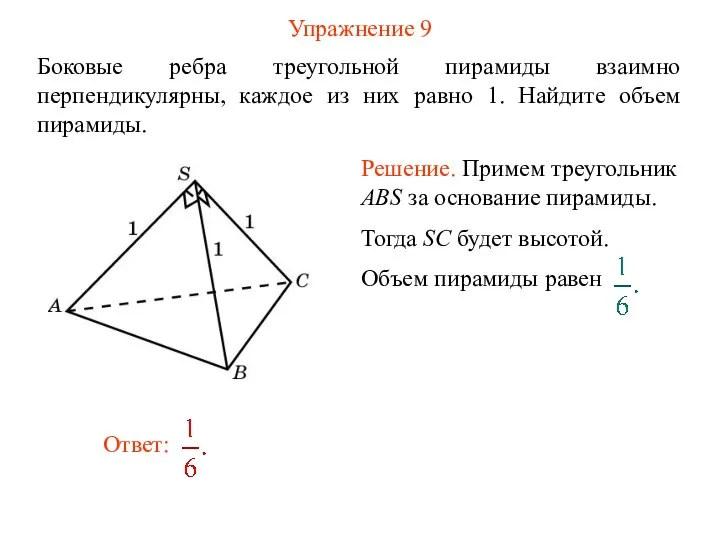
Упражнение 9
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 1. Найдите объем пирамиды.

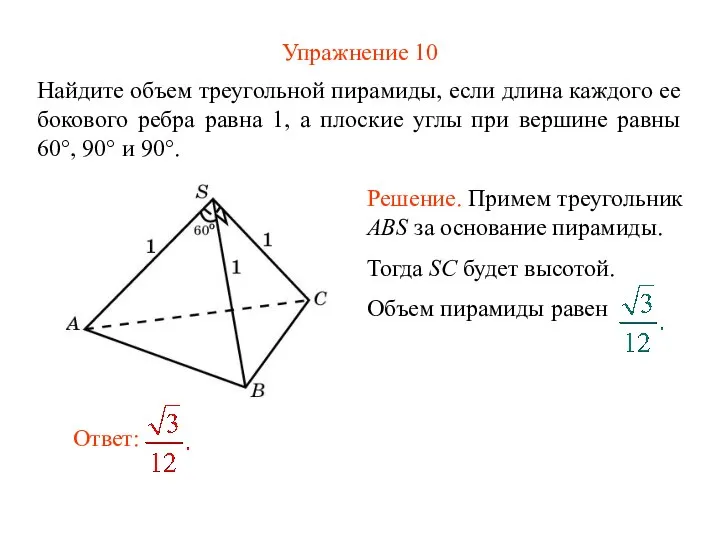
Упражнение 10
Найдите объем треугольной пирамиды, если длина каждого ее бокового ребра равна 1, а плоские углы при вершине равны 60°, 90° и 90°.
Ответ:
Решение. Примем треугольник ABS за основание пирамиды.
Тогда SC будет высотой.
Объем пирамиды равен

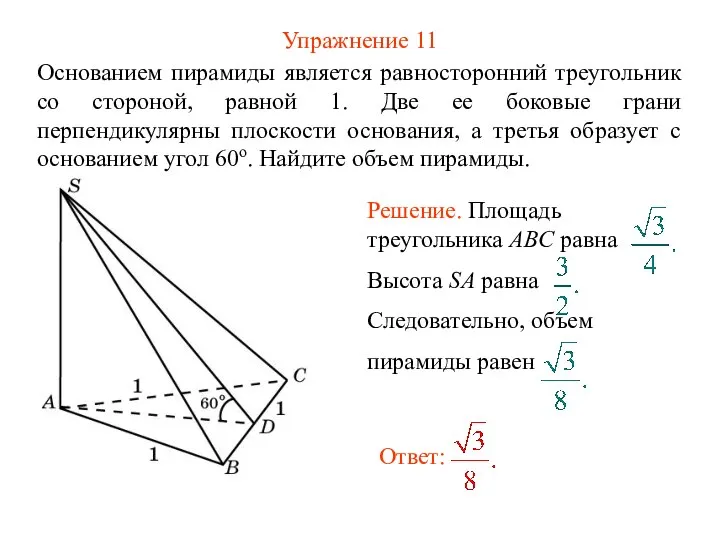
Упражнение 11
Основанием пирамиды является равносторонний треугольник со стороной, равной 1. Две ее боковые грани перпендикулярны плоскости основания, а третья образует с основанием угол 60о. Найдите объем пирамиды.

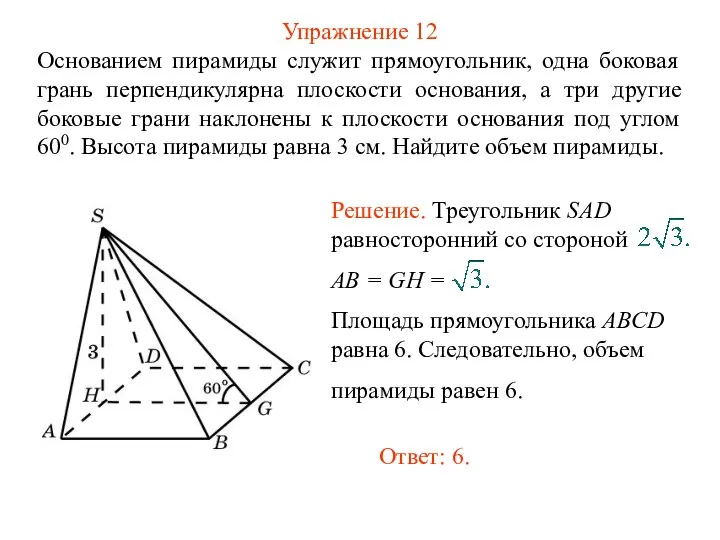
Упражнение 12
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамиды.
Ответ: 6.
Решение. Треугольник SAD равносторонний со стороной
AB = GH =
Площадь прямоугольника ABCD равна 6. Следовательно, объем
пирамиды равен 6.

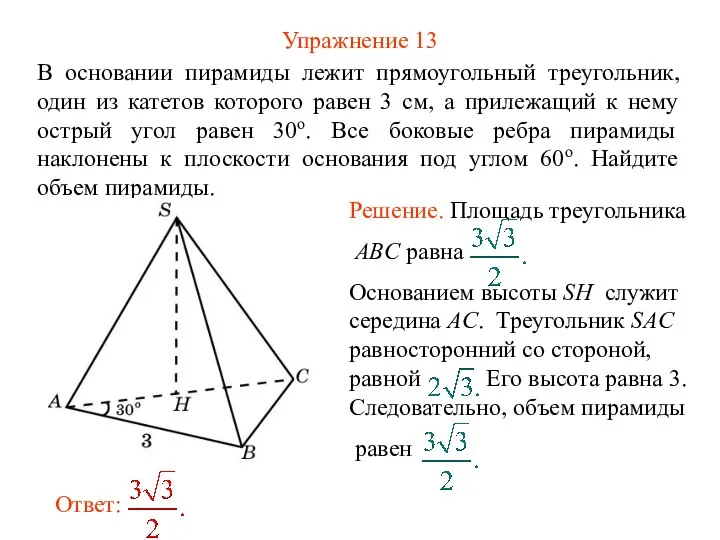
Упражнение 13
В основании пирамиды лежит прямоугольный треугольник, один из катетов которого равен 3 см, а прилежащий к нему острый угол равен 30о. Все боковые ребра пирамиды наклонены к плоскости основания под углом 60о. Найдите объем пирамиды.
Ответ:
Решение. Площадь треугольника
ABC равна
Основанием высоты SH служит середина AC. Треугольник SAC равносторонний со стороной, равной Его высота равна 3. Следовательно, объем пирамиды
равен

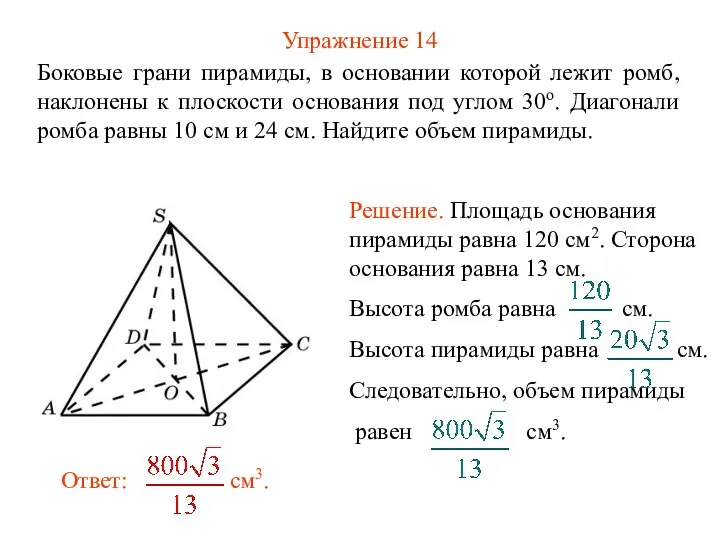
Упражнение 14
Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30о. Диагонали ромба равны 10 см и 24 см. Найдите объем пирамиды.

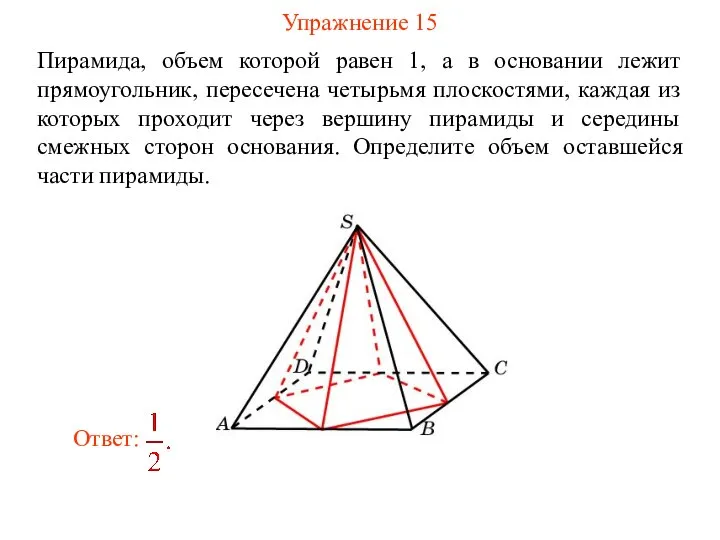
Упражнение 15
Пирамида, объем которой равен 1, а в основании лежит прямоугольник, пересечена четырьмя плоскостями, каждая из которых проходит через вершину пирамиды и середины смежных сторон основания. Определите объем оставшейся части пирамиды.

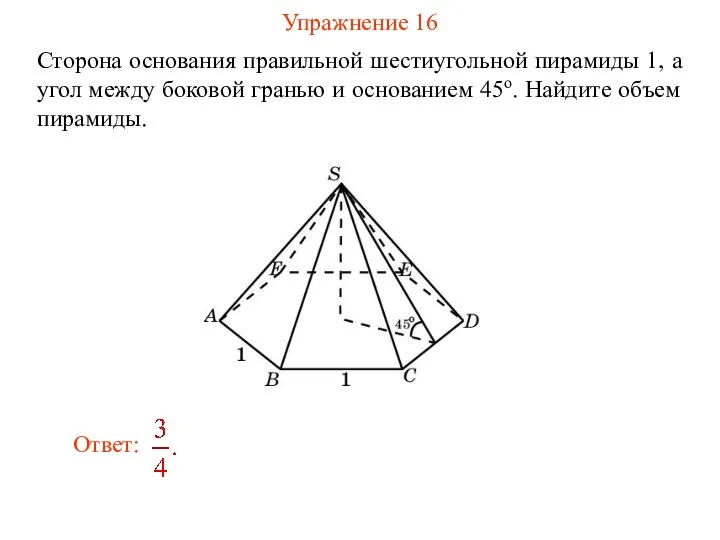
Упражнение 16
Сторона основания правильной шестиугольной пирамиды 1, а угол между боковой гранью и основанием 45о. Найдите объем пирамиды.

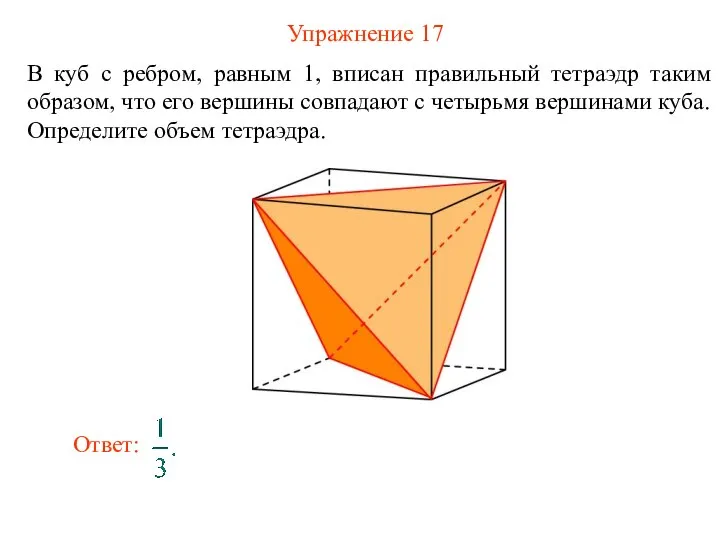
Упражнение 17
В куб с ребром, равным 1, вписан правильный тетраэдр таким образом, что его вершины совпадают с четырьмя вершинами куба. Определите объем тетраэдра.

Упражнение 18
Развертка треугольной пирамиды представляет собой квадрат со стороной 1. Найдите объем этой пирамиды.

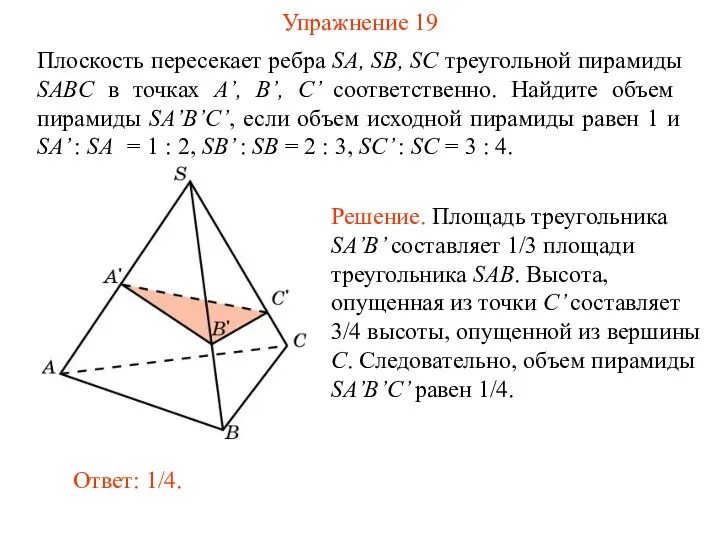
Упражнение 19
Плоскость пересекает ребра SA, SB, SC треугольной пирамиды SABC в точках A’, B’, C’ соответственно. Найдите объем пирамиды SA’B’C’, если объем исходной пирамиды равен 1 и SA’ : SA = 1 : 2, SB’ : SB = 2 : 3, SC’ : SC = 3 : 4.

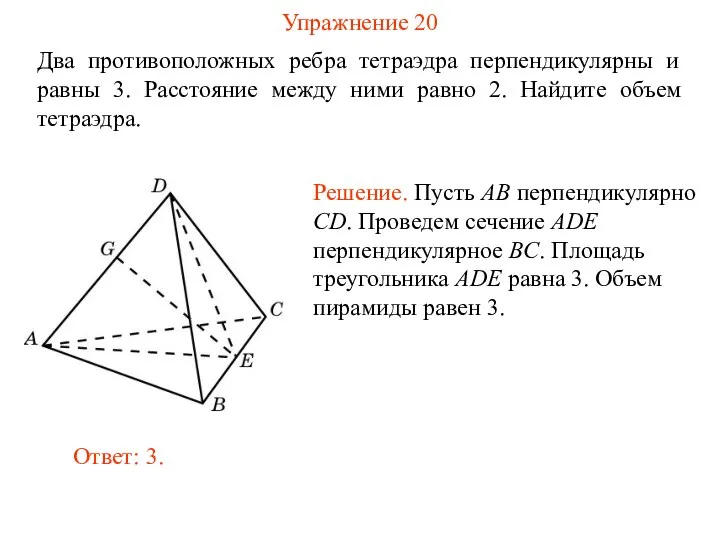
Упражнение 20
Два противоположных ребра тетраэдра перпендикулярны и равны 3. Расстояние между ними равно 2. Найдите объем тетраэдра.

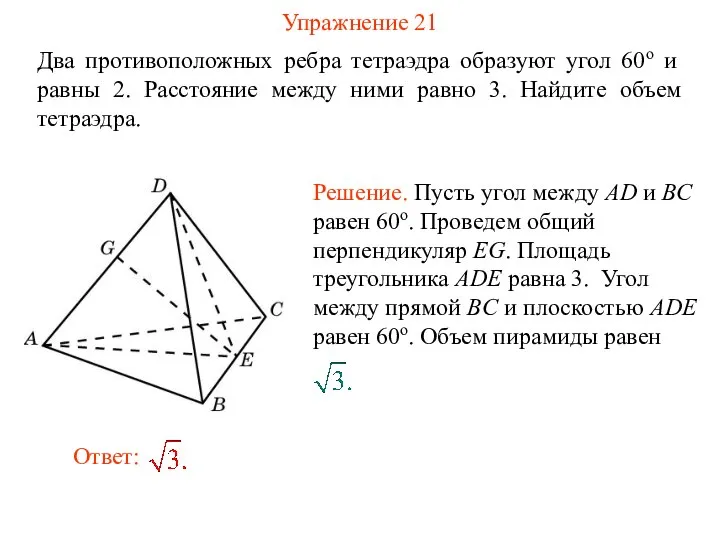
Упражнение 21
Два противоположных ребра тетраэдра образуют угол 60о и равны 2. Расстояние между ними равно 3. Найдите объем тетраэдра.

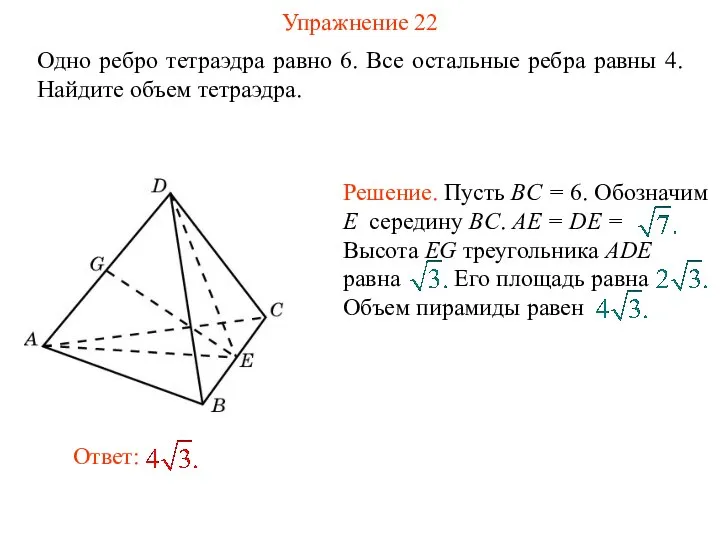
Упражнение 22
Одно ребро тетраэдра равно 6. Все остальные ребра равны 4. Найдите объем тетраэдра.

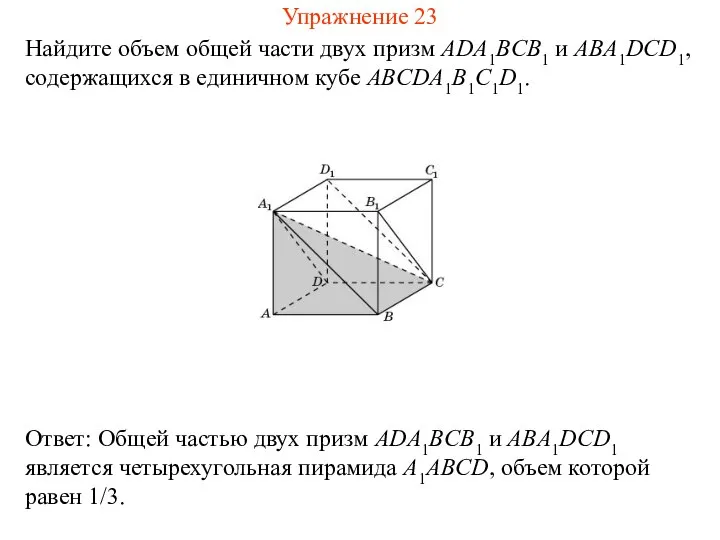
Найдите объем общей части двух призм ADA1BCB1 и ABA1DCD1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 23

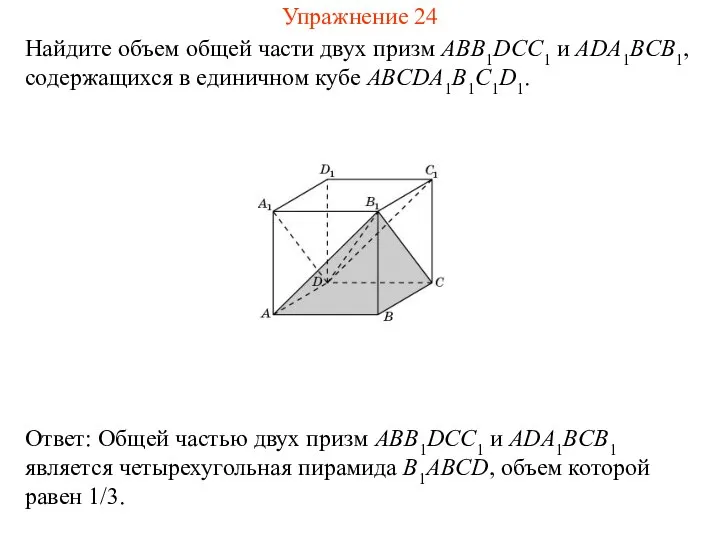
Найдите объем общей части двух призм ABB1DCC1 и ADA1BCB1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 24

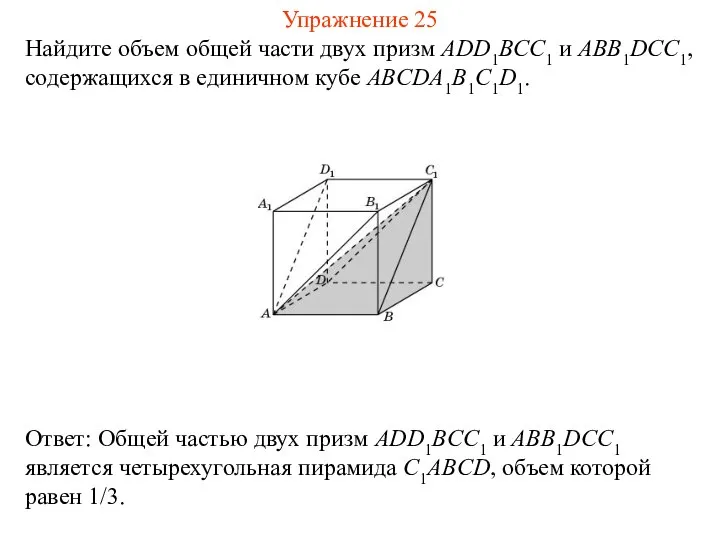
Найдите объем общей части двух призм ADD1BCC1 и ABB1DCC1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 25

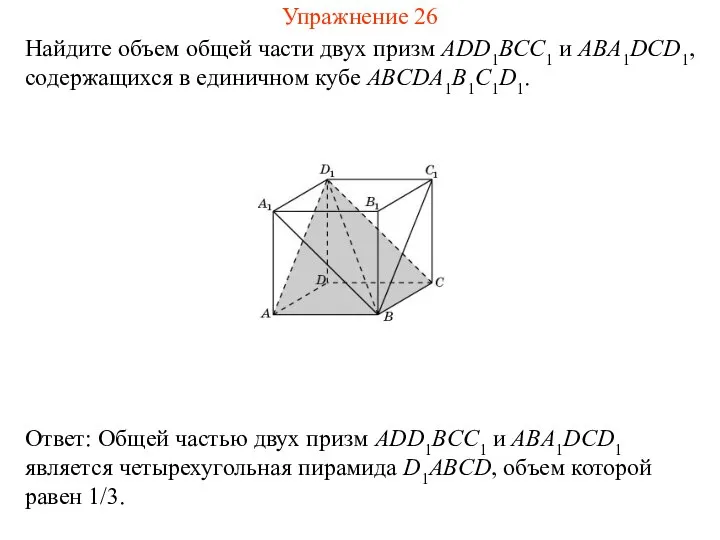
Найдите объем общей части двух призм ADD1BCC1 и ABA1DCD1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 26

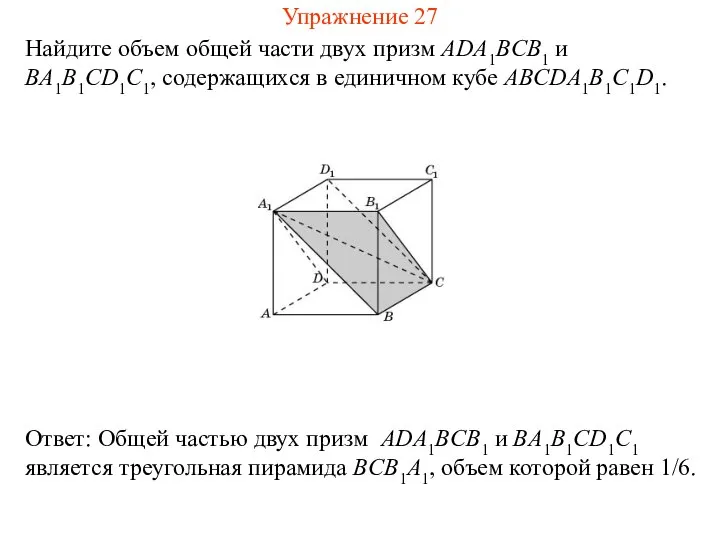
Найдите объем общей части двух призм ADA1BCB1 и BA1B1CD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 27

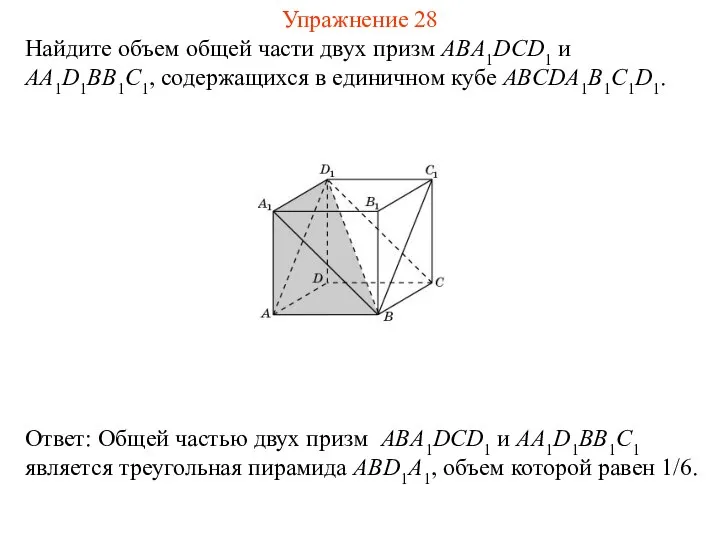
Найдите объем общей части двух призм ABA1DCD1 и AA1D1BB1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 28

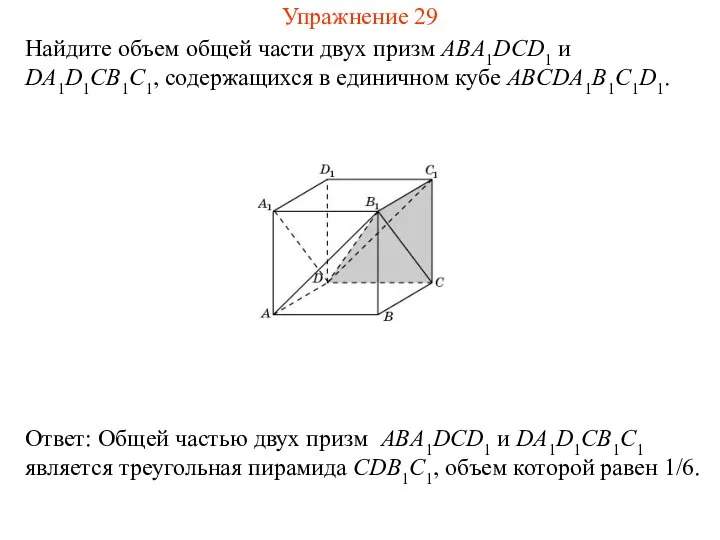
Найдите объем общей части двух призм ABA1DCD1 и DA1D1CB1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 29

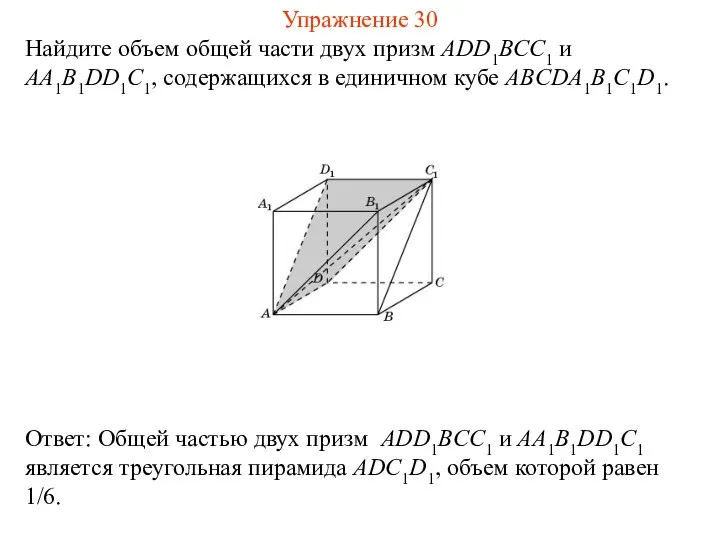
Найдите объем общей части двух призм ADD1BCC1 и AA1B1DD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 30

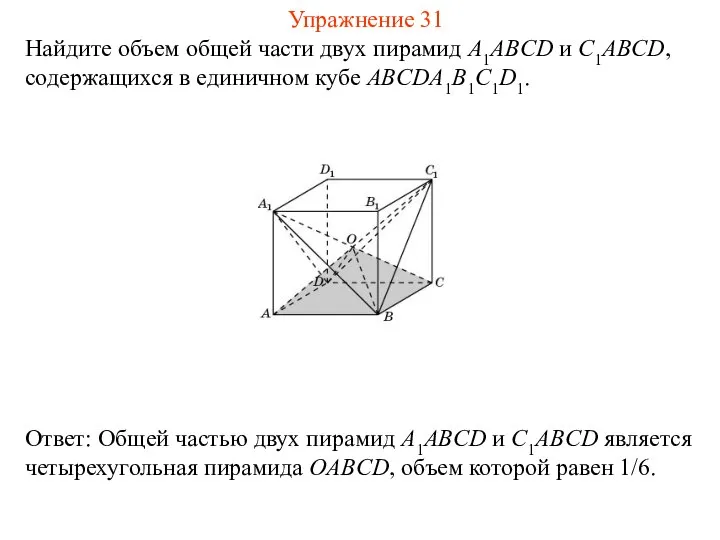
Найдите объем общей части двух пирамид A1ABCD и C1ABCD, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 31

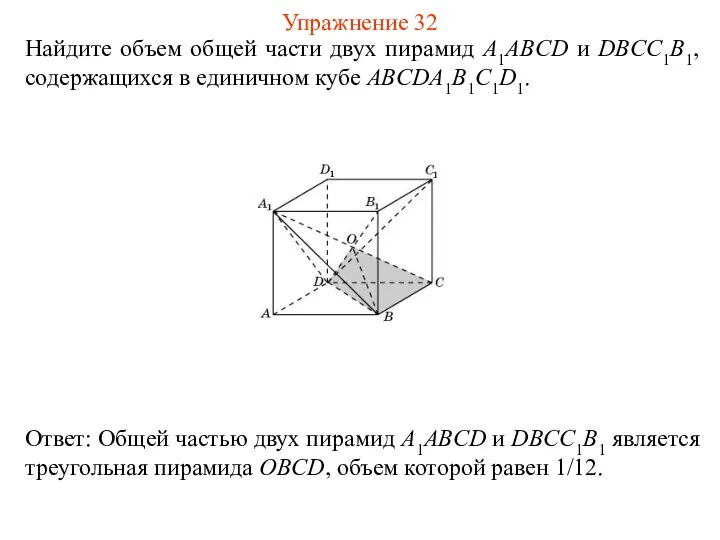
Найдите объем общей части двух пирамид A1ABCD и DBCC1B1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 32

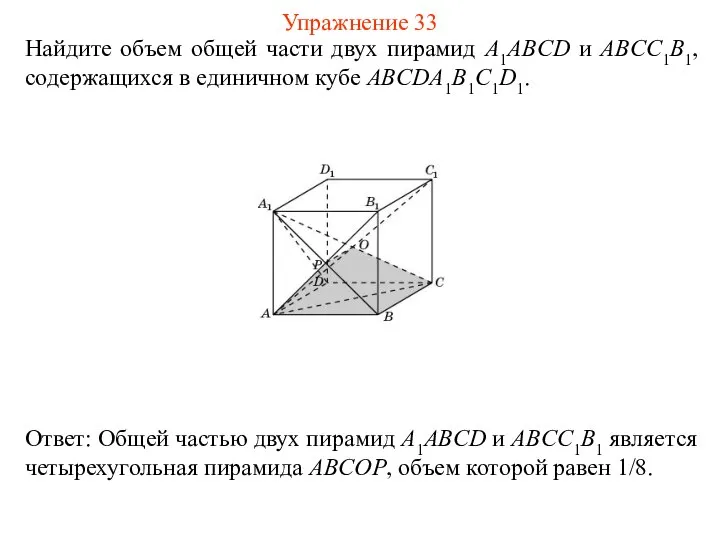
Найдите объем общей части двух пирамид A1ABCD и ABCC1B1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 33

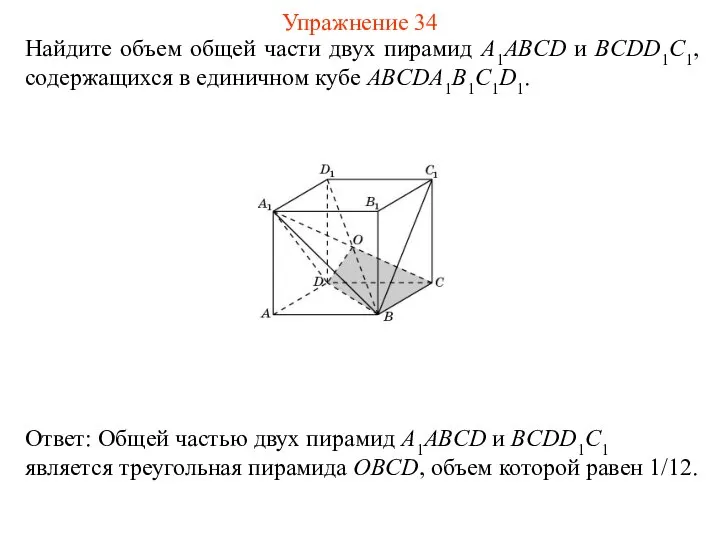
Найдите объем общей части двух пирамид A1ABCD и BCDD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 34

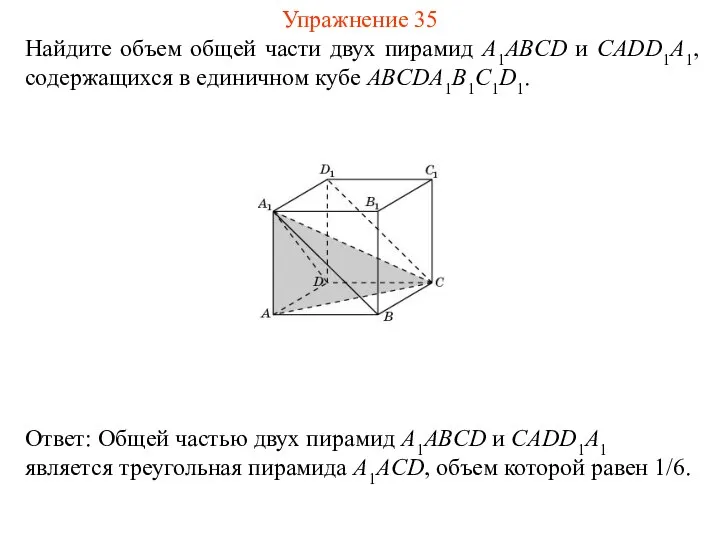
Найдите объем общей части двух пирамид A1ABCD и CADD1A1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 35

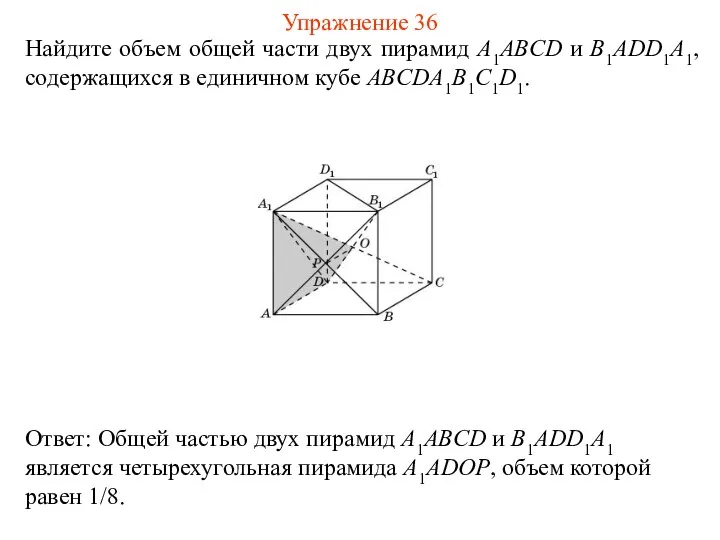
Найдите объем общей части двух пирамид A1ABCD и B1ADD1A1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 36

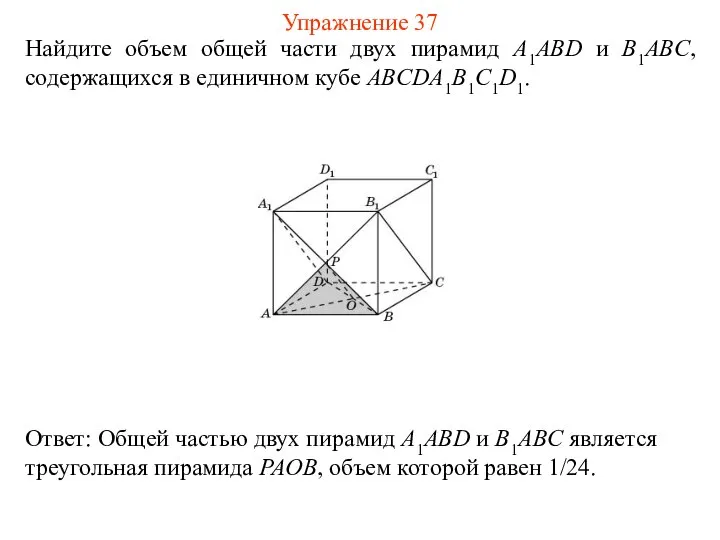
Найдите объем общей части двух пирамид A1ABD и B1ABC, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 37

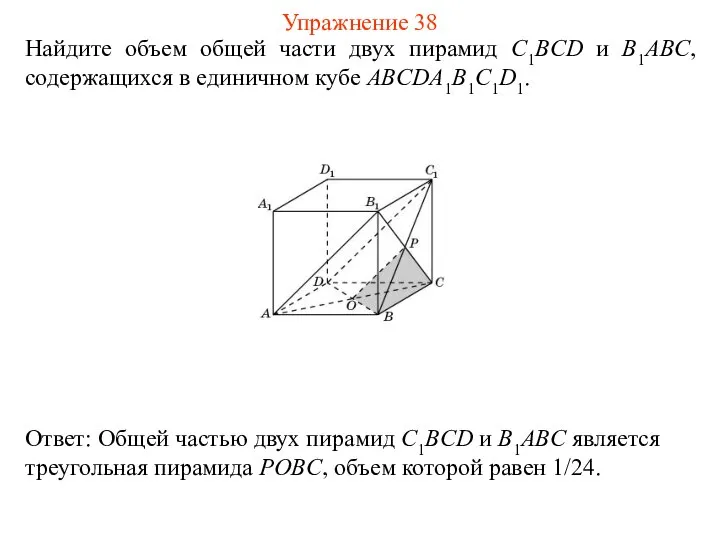
Найдите объем общей части двух пирамид C1BCD и B1ABC, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 38

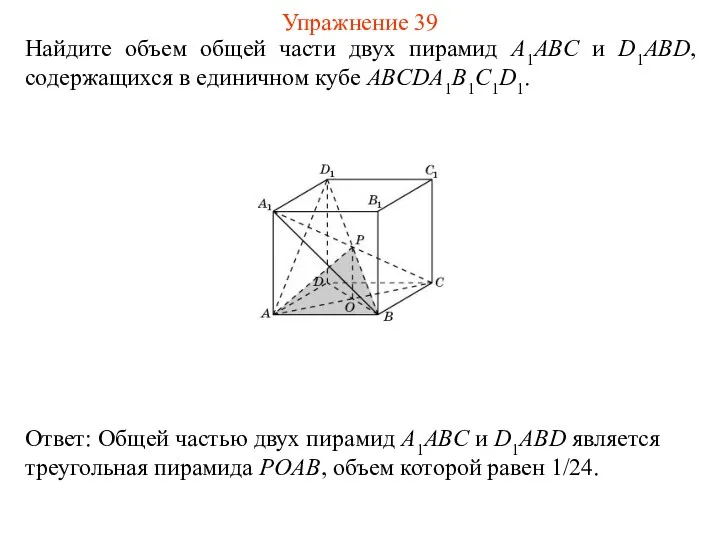
Найдите объем общей части двух пирамид A1ABC и D1ABD, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 39

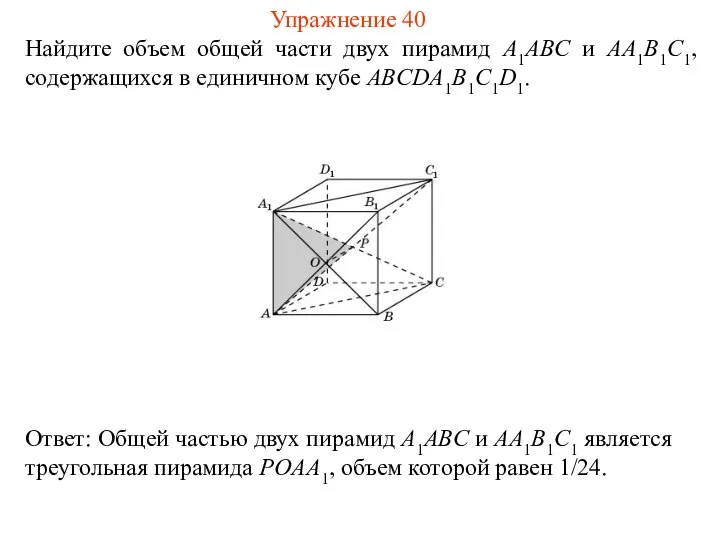
Найдите объем общей части двух пирамид A1ABC и AA1B1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 40

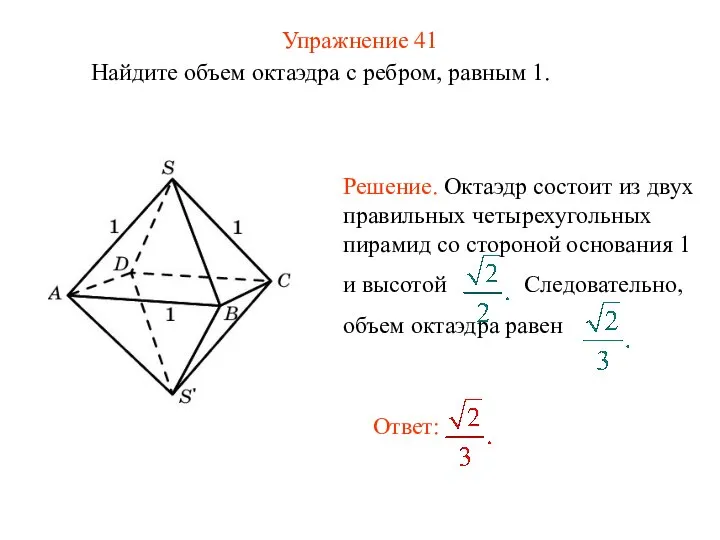
Упражнение 41
Найдите объем октаэдра с ребром, равным 1.

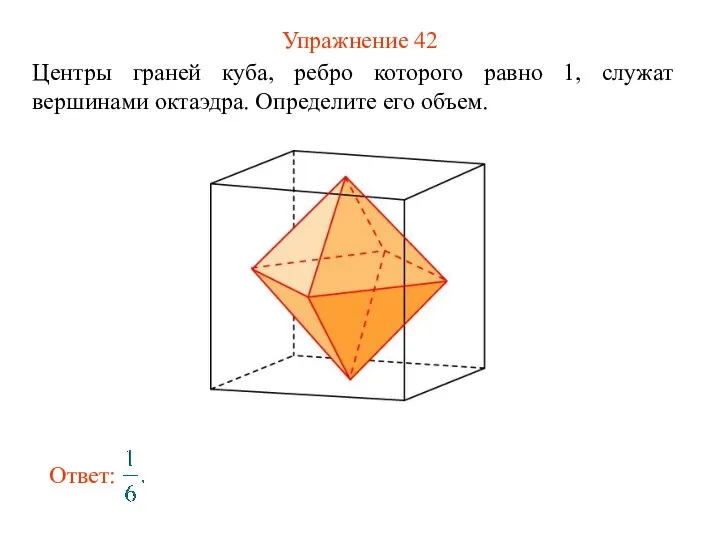
Упражнение 42
Центры граней куба, ребро которого равно 1, служат вершинами октаэдра. Определите его объем.

Упражнение 43
Два куба с ребром a имеют общую диагональ, но один повернут вокруг этой диагонали на угол 60° по отношению к другому. Найдите объем их общей части.
Ответ: Общая часть является правильной 6-й бипирамидой со стороной основания и
Высотой Объем этой
бипирамиды равен

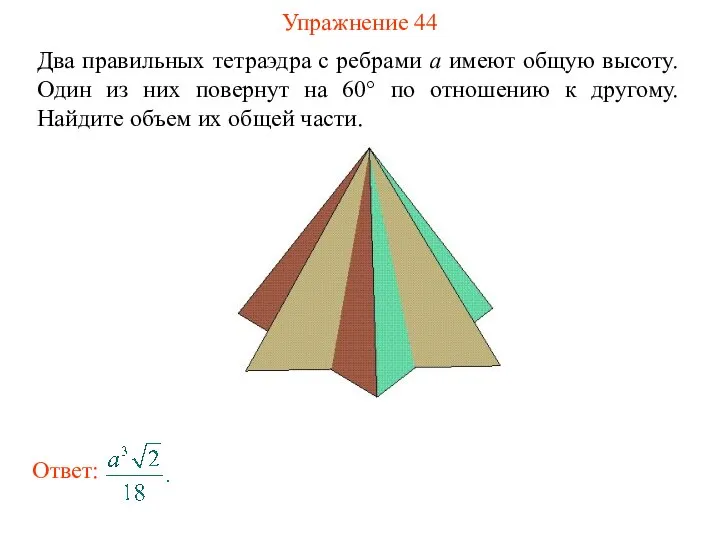
Упражнение 44
Два правильных тетраэдра с ребрами a имеют общую высоту. Один из них повернут на 60° по отношению к другому. Найдите объем их общей части.

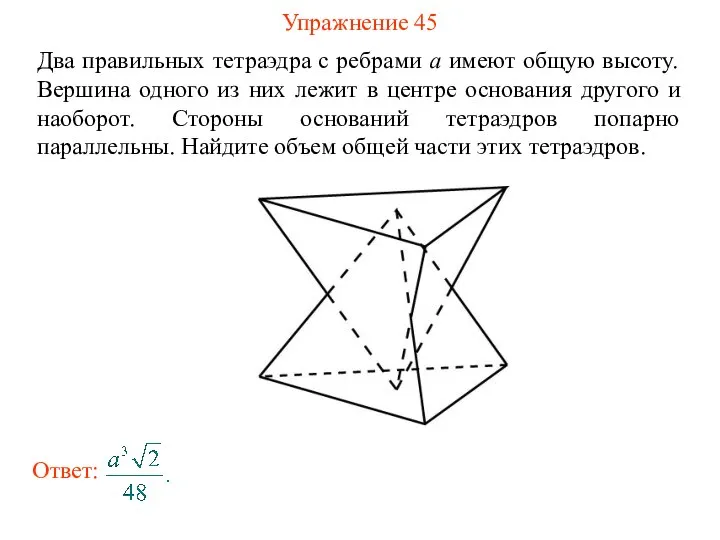
Упражнение 45
Два правильных тетраэдра с ребрами a имеют общую высоту. Вершина одного из них лежит в центре основания другого и наоборот. Стороны оснований тетраэдров попарно параллельны. Найдите объем общей части этих тетраэдров.

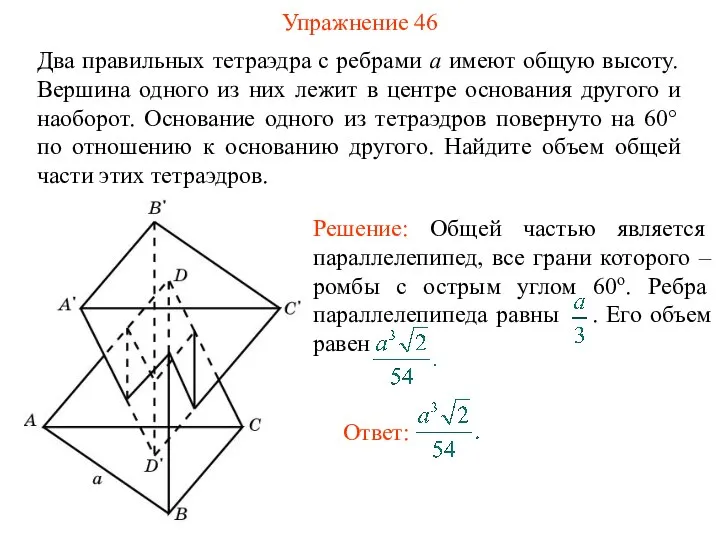
Упражнение 46
Два правильных тетраэдра с ребрами a имеют общую высоту. Вершина одного из них лежит в центре основания другого и наоборот. Основание одного из тетраэдров повернуто на 60° по отношению к основанию другого. Найдите объем общей части этих тетраэдров.

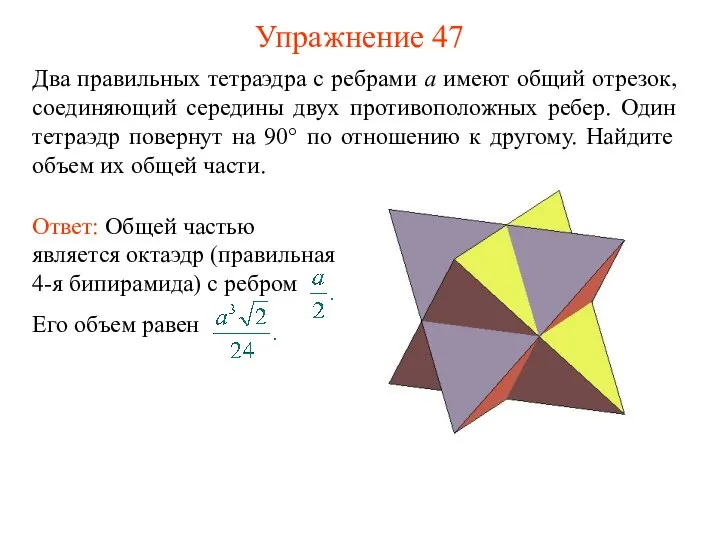
Упражнение 47
Два правильных тетраэдра с ребрами a имеют общий отрезок, соединяющий середины двух противоположных ребер. Один тетраэдр повернут на 90° по отношению к другому. Найдите объем их общей части.
Ответ: Общей частью является октаэдр (правильная 4-я бипирамида) с ребром
Его объем равен