Содержание
- 2. «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят, что пирамида
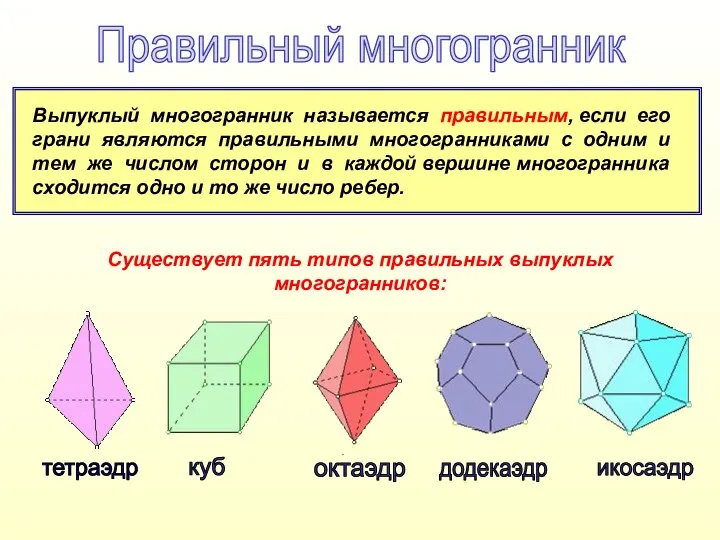
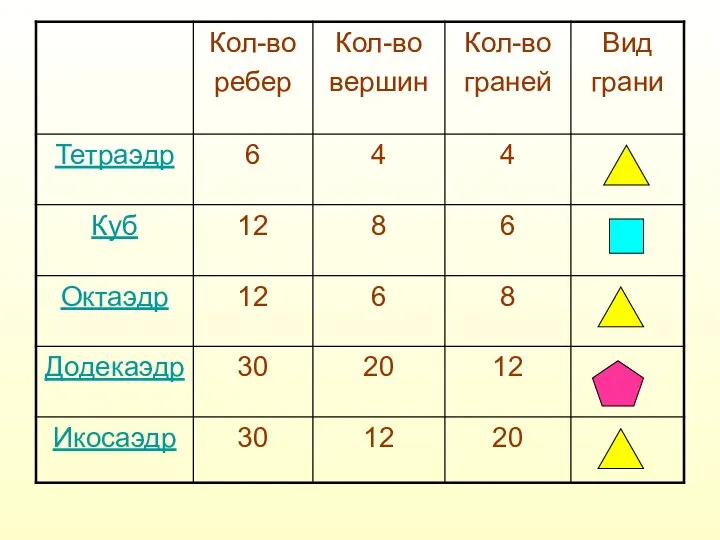
- 3. Выпуклый многогранник называется правильным, если его грани являются правильными многогранниками с одним и тем же числом
- 5. Эта фигура состоит из четырех правильных тре- угольников. Если развернуть их на плоскости, они образуют равносторонний
- 6. Куб — квадрат в трех измерениях, каждая грань которого имеет те же характеристики, что и остальные,
- 7. Собственно говоря, октаэдр является «двойником» куба: если соединить центры смежных граней куба, то получится октаэдр. Октаэдр.
- 8. Додекаэдр — настолько сакральная форма, что во времена Пифагора, если бы кто-то произнес это слово вне
- 9. Если соединить центры граней додека-эдра прямыми линиями, то получится икосаэдр. Соединив центры граней икосаэдра, снова получим
- 10. Историческая справка. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы ,
- 11. Пентаграмме присваивалось способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению
- 12. Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик Эйлер родился в швейцарском городе Базеле
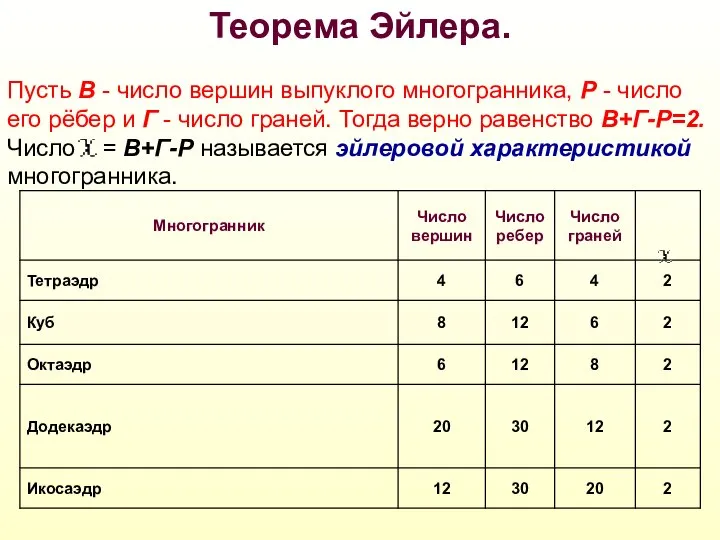
- 13. Теорема Эйлера. Пусть В - число вершин выпуклого многогранника, Р - число его рёбер и Г
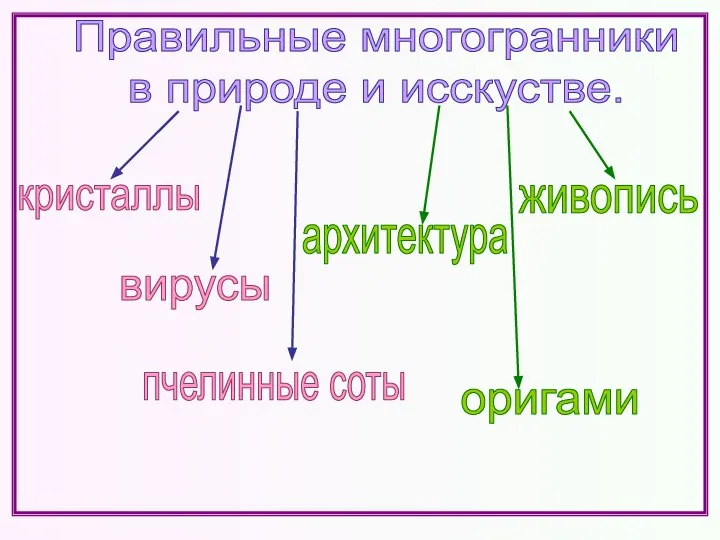
- 14. Правильные многогранники в природе и исскустве. кристаллы вирусы пчелинные соты живопись архитектура оригами
- 15. «Правильные многогранники и природа» Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia
- 16. Использование многогранников в архитектуре Геометрическая конструкция, которую построил солнцеед, целитель и строитель пирамид Николай Николаевич Долгорукий
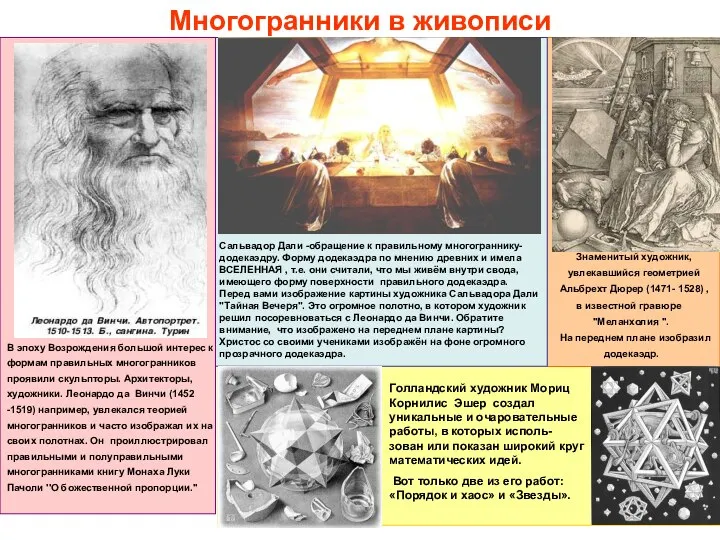
- 17. Многогранники в живописи В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. Архитекторы, художники.
- 18. Оригами. Оригами - увлекательное занятие не только для детей, но и для подростков и даже взрослых!
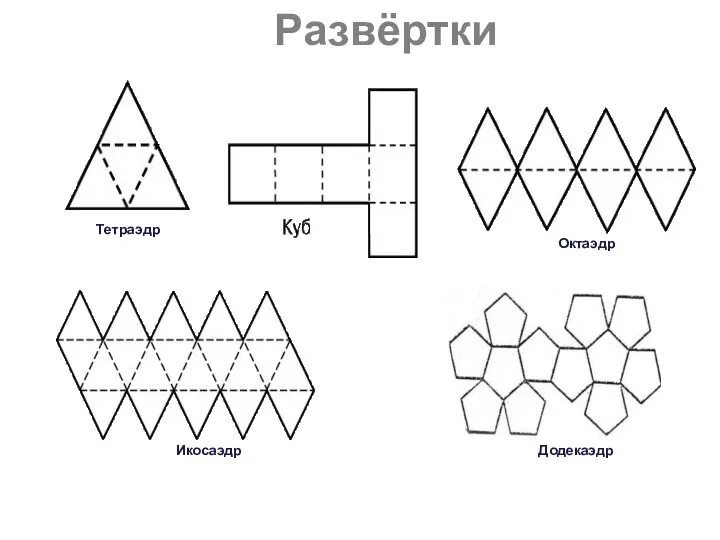
- 19. Развёртки
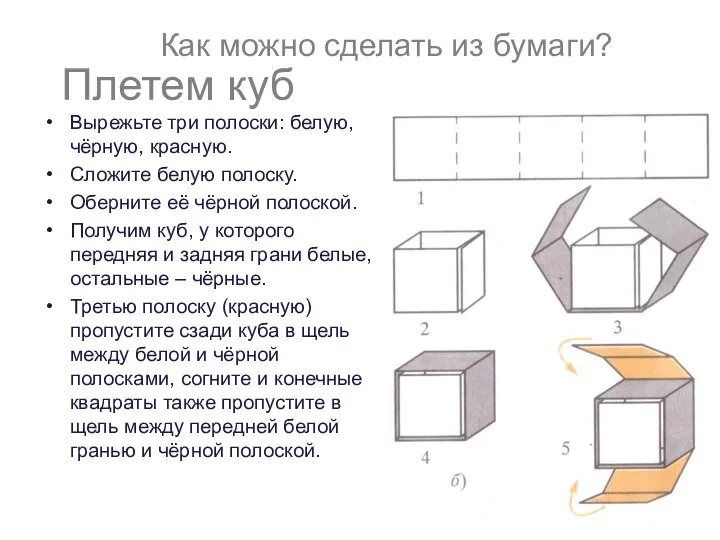
- 20. Вырежьте три полоски: белую, чёрную, красную. Сложите белую полоску. Оберните её чёрной полоской. Получим куб, у
- 22. Скачать презентацию












 Задачи про виноград и изюм
Задачи про виноград и изюм Многогранники. Правильные многогранники
Многогранники. Правильные многогранники Свойство биссектрисы угла
Свойство биссектрисы угла Площадь фигур - какие они
Площадь фигур - какие они Презентация на тему Формулы приведения
Презентация на тему Формулы приведения  Дидактическая игра-тест Модуль числа. 6 класс
Дидактическая игра-тест Модуль числа. 6 класс Множества. Операции над ними. Комбинаторика
Множества. Операции над ними. Комбинаторика Пропорция и ее свойства
Пропорция и ее свойства Построение сечений. Задачи
Построение сечений. Задачи Technologia informacyjna
Technologia informacyjna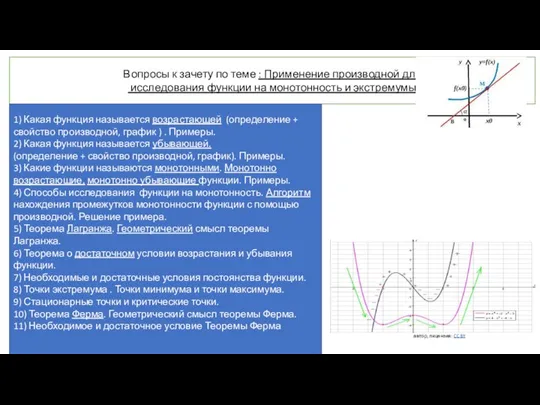 Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Решение задач
Решение задач Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Вычисление производных. Формулы дифференцирования
Вычисление производных. Формулы дифференцирования Свойства функций. Монотонность
Свойства функций. Монотонность Сечения многогранников
Сечения многогранников Оценочная и сравнительная классификация алгоритмов
Оценочная и сравнительная классификация алгоритмов Веселые примеры
Веселые примеры Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Углы, диаграммы, факториал. Повторение
Углы, диаграммы, факториал. Повторение Презентация на тему Объем призмы
Презентация на тему Объем призмы  Устная работа
Устная работа Умножение на 2
Умножение на 2 Презентация на тему Тригонометрические уравнения
Презентация на тему Тригонометрические уравнения  Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Число и цифра 3
Число и цифра 3 Функции. ЕГЭ
Функции. ЕГЭ