Множества натуральных чисел

1) Что такое число?
Число — абстракция, используемая для количественной характеристики объектов.
2) Когда возникли числа?
Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.
3) Какие виды чисел вам известны?
Натуральные, целые, рациональные, действительные
А) Как появились натуральные числа?
Их появление связано с необходимостью ведения счета предметов.
Множество натуральных чисел обозначается латинской буквой N ={1,2,3,....}

Б) Как появились целые числа?
Чтобы любое уравнение х+а=в имело корни, положительных чисел недостаточно и поэтому возникает потребность ввести отрицательные числа и нуль.
Человек пришел к выводу, что необходимо расширение понятия числа.
Множество целых чисел состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0.
Целые числа обозначаются латинской буквой
Z={…-3,-2,-1,0,1,2,3,....}.

В) Как появились рациональные числа?
Одна из причин введения рациональных чисел обусловлена требованием, чтобы всякое линейное уравнение ax = b было разрешимо т.к. в области целых чисел линейное уравнение разрешимо лишь в том случае, когда b делится нацело на a.
Рациональные числа – это числа, представимые в виде дроби , где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные.

Г) Как появились действительные числа?
Одна из причин расширения множества рациональных чисел
до множества действительных чисел была связана с тем, чтобы выразить длину диагонали квадрата со стороной 1. Известно, что она равна
Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными.
.

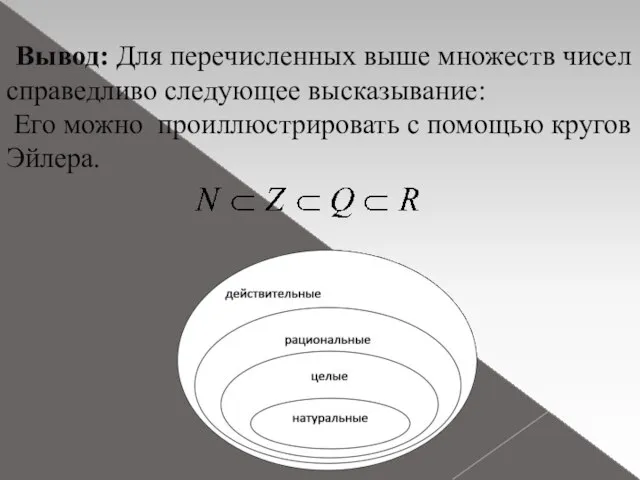
Вывод: Для перечисленных выше множеств чисел справедливо следующее высказывание:
Его можно проиллюстрировать с помощью кругов Эйлера.

Первичное усвоение знаний
(Исторические сведения развития понятия числа)

Что это за числа, как их «потрогать руками» – все это вопросы, не имеющие ответа. Мы просто договорились считать, что они есть. И вполне естественно, что такие числа были названы в 1637 г. французским математиком Декартом мнимыми, т.е. «нереальными».
Кроме привычных действительных (буквально – «реально существующих») чисел нам приходится рассматривать еще числа вида – положительное действительное.

Число , играющее роль «строительного блока» в мире мнимых чисел, называют мнимой единицей.

В 1777 г. Л. Эйлер, предложил использовать первую букву французского слова (imaginare) – мнимый для обоз-начения числа (мнимой единицы).
Эйлер

Этот символ вошел во всеобщее употребление благодаря К.Гауссу. Термин «комплексные числа» также был введен Гауссом в 1831 году.
Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т.д., образующих единое целое.
К.Гаусс

Изложение нового материала

Комплексным числом z называется число вида z = a+bi,
где a и b – действительные числа,
i –мнимая единица;
число a называется действительной частью (Re z) комплексного числа z,
число b называется мнимой частью (Im z) комплексного числа z.
z = a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение

Определение: Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимой единице.
z1 = a1+b1i и z2 = a2+b2i
z1 = z2 a1+b1i = a2+b2i ,
если a1= a2, b1= b2
Равенство комплексного числа нулю:
z = a+bi=0, если a=0, b=0

Определение: Два комплексных числа называются сопряженными, если они отличаются только знаками коэффициента при мнимой единице.
z = a + bi z = a - bi
Определение: Два комплексных числа называется противоположными, если они в сумме дают нуль.

Действия над комплексными числами в алгебраической форме
Сложение комплексных чисел
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части
z1+ z2 = (a1+b1i)+ (a2+b2i)=( a1+ a2) +(b1+ b2)* i
Вычитание комплексных чисел
Для того чтобы вычесть из одного комплексного числа другое, нужно вычесть действительные и мнимые части соответственно
z1 - z2 = (a1+b1i) - (a2+b2i)=( a1+ a2) - (b1+ b2)* i

Умножение комплексных чисел
Комплексные числа перемножаются как двучлены, при этом учитывается, что
i2 = -1.
z1* z2 = (a1+b1i) * (a2+b2i)
Деление комплексных чисел
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение
z1 / z2= z1* z2 / z2* z2=
(a1+b1i) * (a2-b2i) / (a2+b2i) * (a2-b2i)

Рассмотрим примеры
Пример 1
Сложить два комплексных числа
z1= 2+5i, z2= 4-3i,
z = 6+2i
Пример 2
Найти разности комплексных чисел, если
z1=10-25i, z2=1-3i
Действие аналогично сложению,
единственная особенность состоит в том,
что вычитаемое нужно взять в скобки,
а затем – стандартно раскрыть эти скобки со сменой знака:
z =10-25i - (1-3i) = 9-22i

Пример 3
Найти произведение комплексных чисел z1=1- i z2=3+6i
Ответ: z=9+3i
Пример 4
Найти отношение z1=3+ i и z2=4+i
Умножаем числитель и знаменатель на (4 - i)

Решение квадратных уравнений в поле комплексных чисел
ax2 + bx + c = 0
1 cлучай: D>0, 2 корня, х1,2=
2 случай D=0, 1 коре нь, х =
3 cлучай: D<0, 2 корня, х1,2 =

1. Решите уравнение x2 – 4x + 5 = 0.
Решение. D = – 4 < 0,
2. Решите уравнение x2 – x + 10 = 0.
Решение. D = – 39 < 0,
, уравнение имеет мнимые корни:
уравнение имеет мнимые корни: 2+i, 2-i

Решить самостоятельно
Пример 1
Сложить два комплексных числа:
z1=-4+10i z2=5+3i
Пример 2
Найти разности комплексных чисел:
z1=-5+10i z2=1+3i
Пример 3
Найти произведение комплексных чисел:
z1=5-2i z2=1-4i

Решите уравнения:
Решите уравнение x2 – 4x + 13 = 0
2. Решите уравнение x2 – 2x + 15 = 0.

Домашнее задание
1. Даны два комплексных числа z1= (4 + 2i ) и z2=(1 – 3i ). Найти их сумму, разность, произведение и частное.
2. Даны два комплексных числа z1= (5 + 2i ) и z2=(2 – 5i ). Найти их сумму, разность, произведение и частное.
3. Решить уравнения:
1. х2 + (5 – 2i) x + 5(1– i) = 0;
2. х2 + (1 – 2i) х – 2i = 0;

Рефлексия
Как вы оцениваете свою работу на занятии?
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке