компьютера на уроке (не более 20 минут).
- Мы ввели понятие квадратного уравнения. Какой способ мышления нами использовался, по вашему мнению: индукция или дедукция?
-Кого из ярких приверженцев дедуктивного метода вы знаете?
(Шерлок Холмс)
- Чем его способ рассуждения отличен от нашего?
(у него есть совершенное событие – преступление)
- Мы шли в своих рассуждениях от частного к общему, такой способ мышления называется индукцией.
- Такому способу мышления соответствует логическая операция обобщение – это форма приращения знания- Такому способу мышления соответствует логическая операция обобщение – это форма приращения знания путём мысленного перехода от частного- Такому способу мышления соответствует логическая операция обобщение – это форма приращения знания путём мысленного перехода от частного к общему.
Введение понятия может осуществляться двумя способами:
1). Индуктивным с последующим осознанием, что использовался способ мышления индукция ( от частного к общему).
2). Дедуктивное введение понятия (от общего к частному) :
А) показать на практике;
Б) Ввести понятии;
В) Предложить прочитать учебник























 Шкала отношений
Шкала отношений Параметр на ЕГЭ
Параметр на ЕГЭ Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт
Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт Презентация на тему Тренажер по формулам сокращенного умножения
Презентация на тему Тренажер по формулам сокращенного умножения  Степень с рациональным показателем. Самостоятельная работа
Степень с рациональным показателем. Самостоятельная работа Решение неравенств
Решение неравенств На лесной поляне
На лесной поляне Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма Рисуем параллелепипед
Рисуем параллелепипед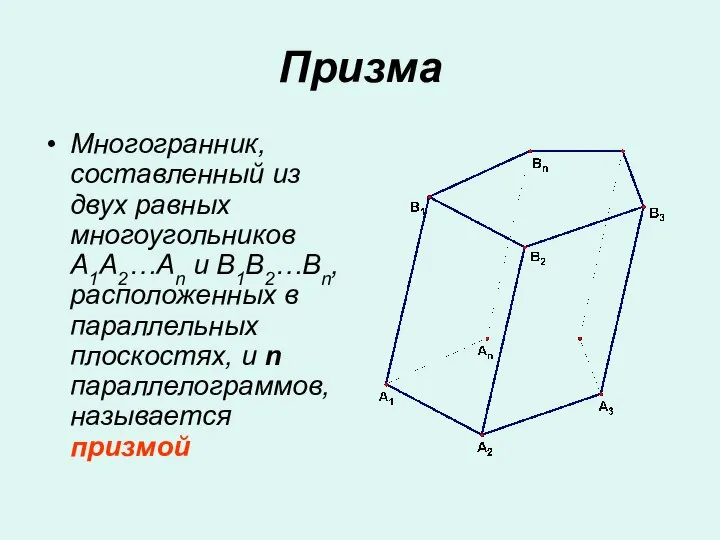 Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Занятие 01.10+Задания для п.р
Занятие 01.10+Задания для п.р Графика. Абстракция.1 тема
Графика. Абстракция.1 тема Теорема Муавра-Лапласа
Теорема Муавра-Лапласа Увеличение и уменьшение на несколько %
Увеличение и уменьшение на несколько % Длина окружности. Площадь круга
Длина окружности. Площадь круга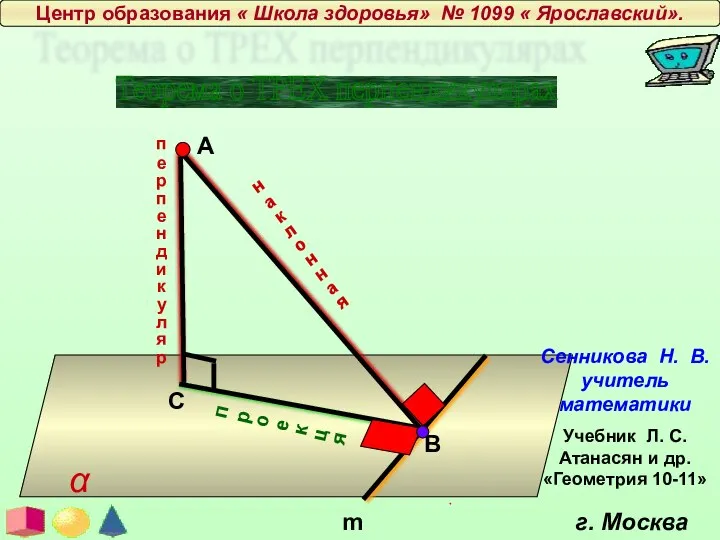 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Длина окружности
Длина окружности Построение таблиц истинности
Построение таблиц истинности Тест Смешанные числа
Тест Смешанные числа Веселая математика
Веселая математика Параллельные прямые
Параллельные прямые Формирование счетных навыков. Требования к счетной деятельности
Формирование счетных навыков. Требования к счетной деятельности Планиметрия. Обзор методички
Планиметрия. Обзор методички Системы линейных уравнений
Системы линейных уравнений Презентация на тему Угол поворота. Радианная мера угла
Презентация на тему Угол поворота. Радианная мера угла  Умозаключение по аналогии
Умозаключение по аналогии Многогранники в биологии
Многогранники в биологии Координаты и векторы
Координаты и векторы