Слайд 21. Последовательности
Если последовательность имеет предел, она называется
Сходящейся последовательностью.

Слайд 3Свойства сходящих последовательностей.
Сходящаяся последовательность фундаментальна.
Предел сходящейся последовательности единственен.
Сходящаяся последовательность ограничена.
Из любой ограниченной

последовательности можно выбрать сходящуюся подпоследовательность.
(Теорема Больцано-Вейерштрасса)
Слайд 4Функции. Предел функции. Непрерывные функции.
Определение.
Число А называется пределом f(x) при х→а, если
∀?>0

∃?>0 |x-a|Число А называется пределом f(x) при х→а, если
∀{xn}: xn→a ⇒ f(xn)→A, n→∞



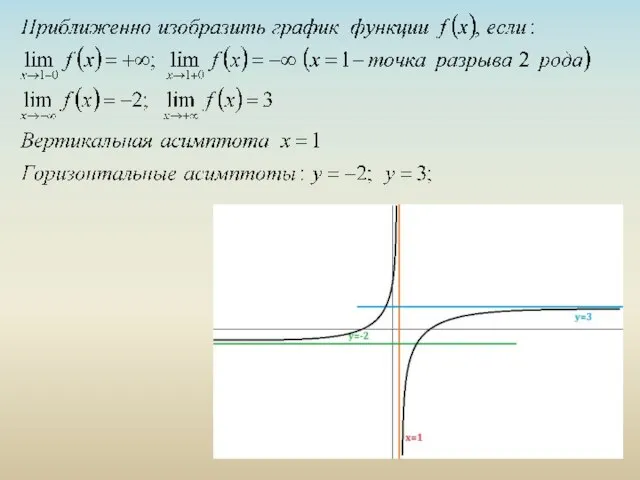

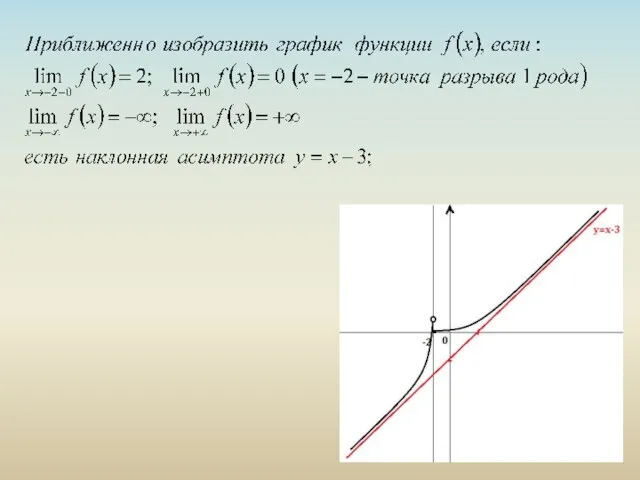
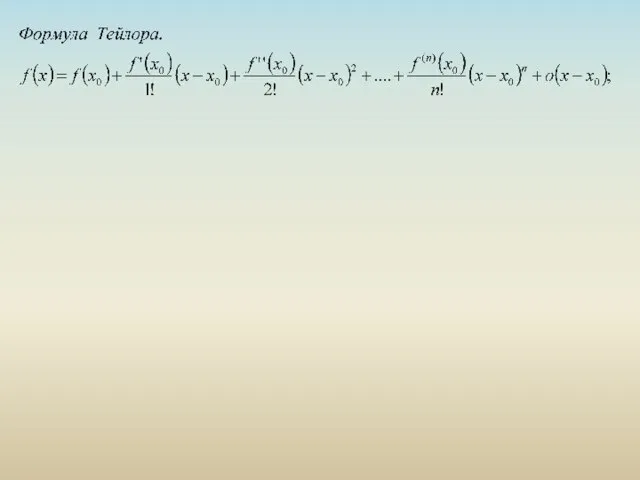

 Десятичная запись дробей
Десятичная запись дробей Задачи на построение
Задачи на построение Геометрия в жизни человека
Геометрия в жизни человека Показательные уравнения
Показательные уравнения Параллелепипед
Параллелепипед Умножение и деление на однозначное число
Умножение и деление на однозначное число Вариационная форма
Вариационная форма Решение задач по теории вероятности. Подготовка к ГИА
Решение задач по теории вероятности. Подготовка к ГИА Итоги главы 4
Итоги главы 4 Задачи на нахождение площади прямоугольника и трапеции
Задачи на нахождение площади прямоугольника и трапеции Теорема синусов
Теорема синусов Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Генеральная средняя
Генеральная средняя Презентация по математике "Понятие логарифма, основные свойства логарифмов" -
Презентация по математике "Понятие логарифма, основные свойства логарифмов" -  Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений Презентация на тему Евклид
Презентация на тему Евклид  Интересные факты про математику
Интересные факты про математику Презентация на тему Деление обыкновенных дробей
Презентация на тему Деление обыкновенных дробей  Решение логических задач
Решение логических задач Основы линейной алгебры
Основы линейной алгебры Презентация на тему Отношения (6 класс)
Презентация на тему Отношения (6 класс)  В гостях у зайчика (5-6 лет)
В гостях у зайчика (5-6 лет) Комбинаторная задача с шарами
Комбинаторная задача с шарами Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Математика в медицине
Математика в медицине Теорема синусов
Теорема синусов Komplexnye_chisla
Komplexnye_chisla Теорема синусов и косинусов
Теорема синусов и косинусов