Перпендикулярность прямых в пространстве

Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Теорема 3.1 Если две пересекающие
прямые параллельны соответственно
двум перпендикулярным прямым,
то они тоже перпендикулярны.
a
b
a1
b1
C
C1
A
A1
B
B1
Перпендикулярность прямых в пространстве

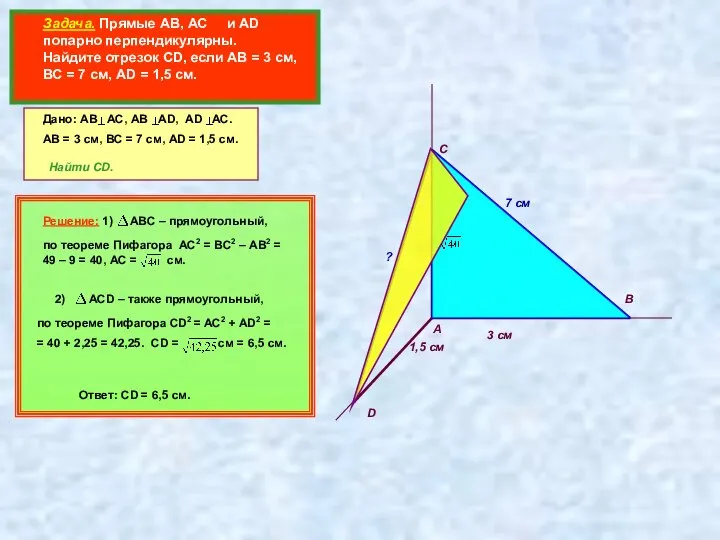
Задача. Прямые АВ, АС и AD попарно перпендикулярны. Найдите отрезок CD, если АВ = 3 см, ВС = 7 см, АD = 1,5 см.
А
В
С
D
Дано: АВ АС, АВ АD, AD AC.
АВ = 3 см, ВС = 7 см, АD = 1,5 см.
3 см
7 см
1,5 см
Найти CD.
?
Решение: 1) АВС – прямоугольный,
по теореме Пифагора АС2 = ВС2 – АВ2 = 49 – 9 = 40, АС = см.
2) АСD – также прямоугольный,
по теореме Пифагора СD2 = AC2 + AD2 =
= 40 + 2,25 = 42,25. CD = cм = 6,5 см.
Ответ: CD = 6,5 см.

Перпендикулярность прямой и плоскости.
Определение. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения данной прямой и плоскости

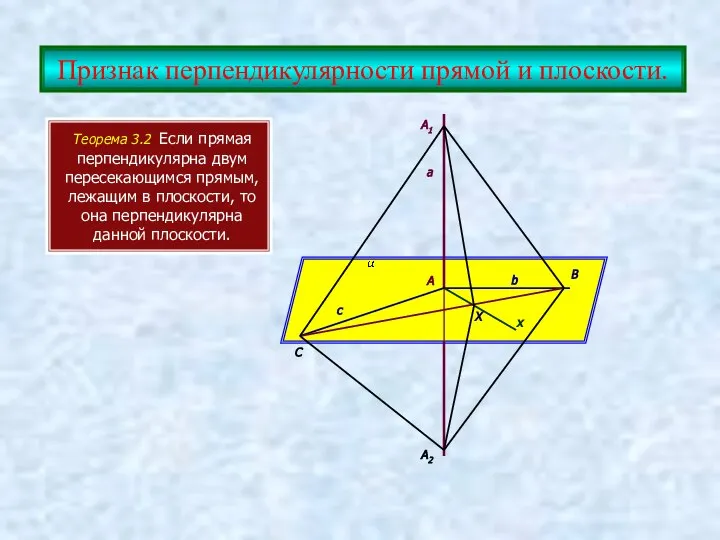
Признак перпендикулярности прямой и плоскости.
Теорема 3.2 Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
a
b
c
x
C
X
B
A
A1
A2

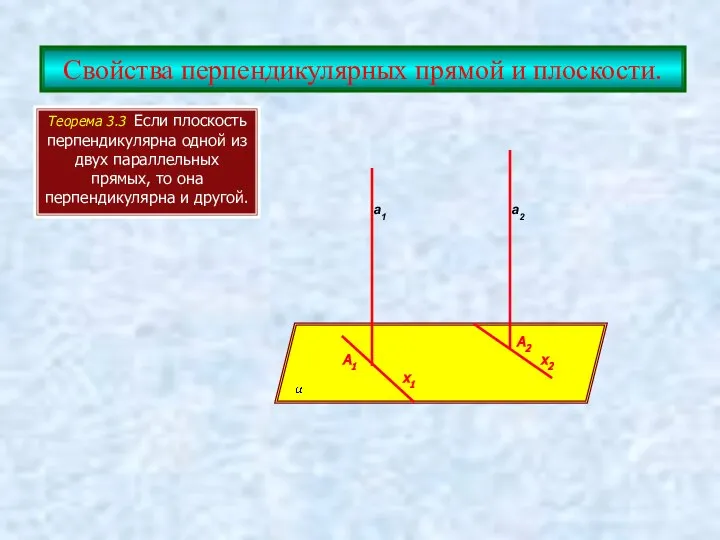
Свойства перпендикулярных прямой и плоскости.
Теорема 3.3 Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
a1
a2
A1
A2
x2
x1

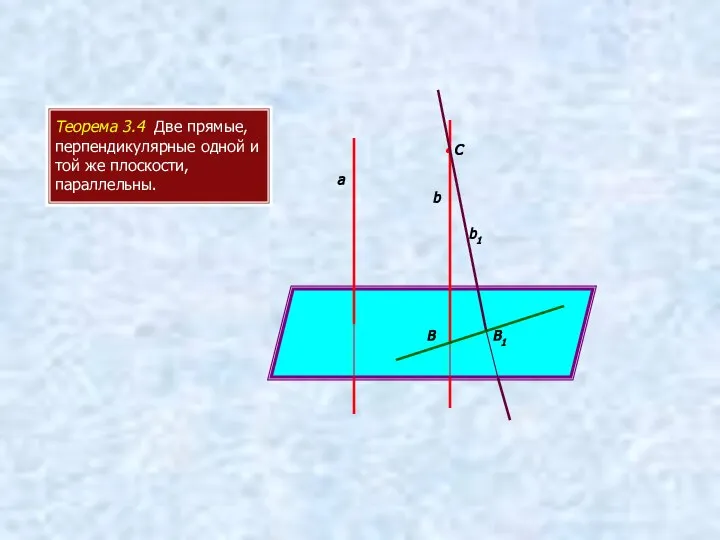
Теорема 3.4 Две прямые, перпендикулярные одной и той же плоскости, параллельны.
а
b
• С
b1
В
В1

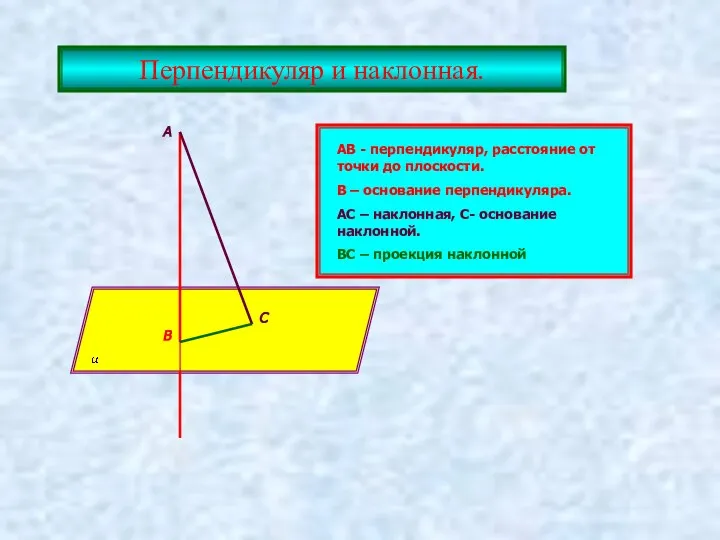
Перпендикуляр и наклонная.
А
В
С
АВ - перпендикуляр, расстояние от точки до плоскости.
В – основание перпендикуляра.
АС – наклонная, С- основание наклонной.
ВС – проекция наклонной