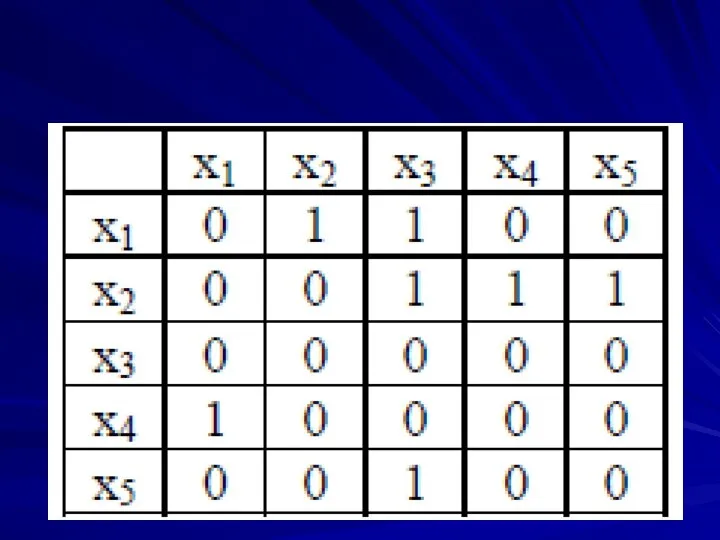
Слайд 21 способо
i-ая строка соответствует элементу хi,
j-ый столбец элементу хj,
на их

пересечении ставится 1, если отношение хiАхj выполнено,
0, если нет.
Так, единица, стоящая на пересечении 4ой строки и 1го столбца, соответствует тому, что игрок х4 выиграл у игрока х1, т.е. <х4Ах1>.
Слайд 4На множестве М отношение
«xi – победитель yj» задано матрицей

Слайд 5Если aij≡0 (i, j = 1,n) , то имеем пустое
отношение, т.е.

такое, которое не выполнено
ни для какой пары хiхj.
Если aij≡1, имеем полное отношение, т.е. отношение, выполненное для всех пар.
Единичная матрица Е задает диагональное отношение, отношение равенства:
<хiАхj>, если хi=хj.
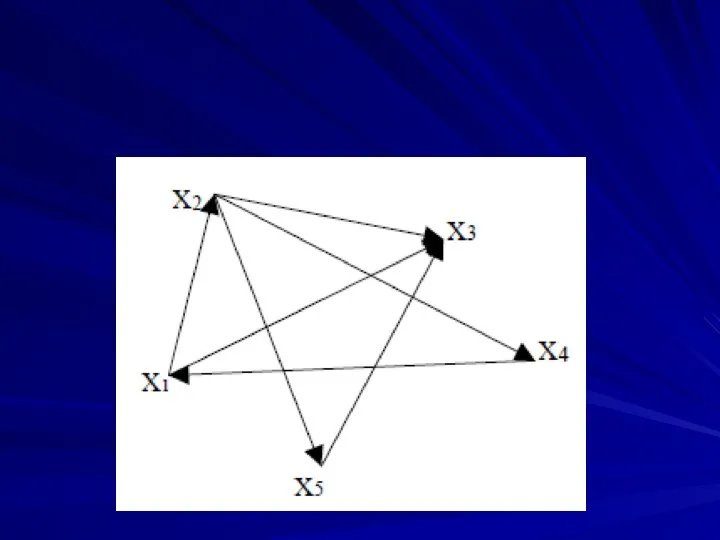
Слайд 62 способ
Элементы множества изобразим точками, проведем стрелку от хi к хj, если

выполнено хiАхj, получим фигуру – ориентированный граф.
Точки х1, х2, х3, х4, х5 – вершины графа, направленные линии – ребра графа.
Слайд 8Свойства отношений:
Отношение А рефлексивно, если оно выполнено между объектом и им самим,

т.е. хАх.
Отношения «быть похожим», «быть знакомым» – рефлексивны. Отношение «быть братом» – нерефлексивно.
Слайд 92) Если отношение А может выполняться лишь для несовпадающих объектов, то оно

антирефлексивно, т.е. из хАу следует, что х≠у.
3) Отношение А называется симметричным, если при выполнении хАу выполнено уАх.
Отношения «быть родственником», «быть похожим на» – симметричны.
Слайд 104) Отношение А называется антисимметричным, если из двух отношений хАу и уАх

хотя бы одно не выполнено. Так, приведенный выше пример: отношение «x – победитель y» – антисимметрично.
Теорема:
если отношение антисимметрично,
то оно антирефлексивно.
Слайд 115) Отношение называется транзитивным, если при выполнении хАу и уАz выполнено хАz.
Примером

является отношение «быть больше (меньше)»:
если х<у и у
Слайд 12Отношение эквивалентности определяется отображением множества Х на множество Y и характеризуется разбиением

множества Х на классы.
Отношение эквивалентности – рефлексивно, симметрично и транзитивно
Слайд 13Отношение А на множестве М называется толерантностью, если оно рефлексивно и симметрично.
Пример:

отношение «быть знакомым»
Отношение А на множестве Х называется отношением порядка, если оно транзитивно и антирефлексивно.
Пример: отношение x
Слайд 14Множество, на котором задано отношение порядка, называется упорядоченным множеством.
Биективное отображение “f” в

упорядоченном множестве Х на упорядоченное множество Y называют соответствием подобия или подобным соответствием, если оно сохраняет порядок.











 Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА
Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА  Системы и совокупности неравенств с одной переменной
Системы и совокупности неравенств с одной переменной Несколько задач про цены
Несколько задач про цены Средние показатели и показатели вариации
Средние показатели и показатели вариации Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике
Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике Касательная и ее свойства
Касательная и ее свойства Операции, функции, выражения
Операции, функции, выражения Вычислительная математика. Практика №2
Вычислительная математика. Практика №2 Переменные величины и их свойства
Переменные величины и их свойства Смешанные числа 5 класс
Смешанные числа 5 класс 04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы
04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы Плоская линия в R2
Плоская линия в R2 Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Понятия много и один. Число и цифра 1
Понятия много и один. Число и цифра 1 Решение задач практического содержания в 9 классе (подготовка к ОГЭ)
Решение задач практического содержания в 9 классе (подготовка к ОГЭ) Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Арифметическая прогрессия. Обобщающий урок
Арифметическая прогрессия. Обобщающий урок Мир глазами эколога
Мир глазами эколога Параллельные прямые
Параллельные прямые Четырехугольники
Четырехугольники Блок случайных событий
Блок случайных событий SW1 Product Manual Product Feature | Q&A
SW1 Product Manual Product Feature | Q&A Учимся писать цифры
Учимся писать цифры Окружность, описанная около треугольника и вписанная в треугольник
Окружность, описанная около треугольника и вписанная в треугольник Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Л 8 Предел функции
Л 8 Предел функции Многогранники в искусстве
Многогранники в искусстве Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами