Слайд 2План занятия
1. Множественный регрессионный анализ.
2. Решение задач.

Слайд 3Про корреляцию & регрессию
Задача корреляционного анализа – определение тесноты и направления связи

между изучаемыми величинами.
В ходе регрессионного анализа определяется аналитическое выражение связи зависимой случайной величины Y (результативный признак) с независимыми случайными величинами Х1, Х2, …Хm (факторами).
Слайд 4Зачем?
Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или

нескольких независимых переменных.
Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес.
Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Слайд 5Задачи регрессионного анализа
При помощи регрессионного анализа возможно решение задачи прогнозирования. Прогнозные значения

вычисляются путем подстановки в уравнение регрессии параметров значений объясняющих переменных.
Основные задачи регрессионного анализа
установление формы зависимости,
определение функции регрессии,
оценка неизвестных значений зависимой переменной.
1 задача - Установление формы зависимости.
Характер и форма зависимости между переменными могут образовывать следующие разновидности регрессии:
положительная линейная регрессия (выражается в равномерном росте функции);
положительная равноускоренно возрастающая регрессия;
положительная равнозамедленно возрастающая регрессия;
отрицательная линейная регрессия (выражается в равномерном падении функции);
отрицательная равноускоренно убывающая регрессия;
отрицательная равнозамедленно убывающая регрессия.
Однако описанные разновидности обычно встречаются не в чистом виде, а в сочетании друг с другом. В таком случае говорят о комбинированных формах регрессии.
Слайд 6Задачи регрессионного анализа
2 задача - Определение функции регрессии.
Вторая задача сводится к выяснению

действия на зависимую переменную главных факторов или причин, при неизменных прочих равных условиях, и при условии исключения воздействия на зависимую переменную случайных элементов. Функция регрессии определяется в виде математического уравнения того или иного типа.
3 задача - Оценка неизвестных значений зависимой переменной.
Оценка значений зависимой переменной внутри рассматриваемого интервала исходных данных, т.е. пропущенных значений; при этом решается задача интерполяции.
Оценка будущих значений зависимой переменной, т.е. нахождение значений вне заданного интервала исходных данных; при этом решается задача экстраполяции.
Обе задачи решаются путем подстановки в уравнение регрессии найденных оценок параметров значений независимых переменных. Результат решения уравнения представляет собой оценку значения целевой (зависимой) переменной.
Слайд 7Уравнение регрессии -
это форма связи результативного признака Y с факторами Х1, Х2,

…Хm.
В зависимости от типа выбранного уравнения различают линейную и нелинейную (квадратичную, экспоненциальную, логарифмическую и т.д.) регрессию.
Слайд 8Парная и множественная регрессия
В зависимости от числа взаимосвязанных признаков различают парную и

множественную регрессию.
Парная – исследуется связь между двумя признаками (результативным и факторным).
Множественная (многофакторная) – между тремя признаками (результативным и несколькими факторными).
Слайд 9Уравнение регрессии
Уравнение регрессии выглядит следующим образом: Y=a+b*X
При помощи этого уравнения переменная Y

выражается через константу a и угол наклона прямой (или угловой коэффициент) b, умноженный на значение переменной X. Константу a также называют свободным членом, а угловой коэффициент - коэффициентом регрессии или B-коэффициентом.
В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой.
Остаток - это отклонение отдельной точки (наблюдения) от линии регрессии (предсказанного значения).
Для решения задачи регрессионного анализа в MS Excel выбираем в меню Сервис "Пакет анализа" и инструмент анализа "Регрессия". Задаем входные интервалы X и Y. Входной интервал Y - это диапазон зависимых анализируемых данных, он должен включать один столбец. Входной интервал X - это диапазон независимых данных, которые необходимо проанализировать. Число входных диапазонов должно быть не больше 16.
Слайд 10Этапы регрессионного анализа
1. Задание аналитической формы уравнения регрессии и определение параметров регрессии.
2.

Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии.
3. Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.
Слайд 11Предположения, на которые опирается РА
Предположение линейности, т.е. предполагается, что связь между рассматриваемыми

переменными является линейной. Так, в рассматриваемом примере мы построили диаграмму рассеивания и смогли увидеть явную линейную связь. Если же на диаграмме рассеивания переменных мы видим явное отсутствие линейной связи, т.е. присутствует нелинейная связь, следует использовать нелинейные методы анализа.
Предположение о нормальности остатков. Оно допускает, что распределение разницы предсказанных и наблюдаемых значений является нормальным. Для визуального определения характера распределения можно воспользоваться гистограммами остатков.
При использовании регрессионного анализа следует учитывать его основное ограничение. Оно состоит в том, что регрессионный анализ позволяет обнаружить лишь зависимости, а не связи, лежащие в основе этих зависимостей.
Регрессионный анализ дает возможность оценить степень связи между переменными путем вычисления предполагаемого значения переменной на основании нескольких известных значений.
Слайд 12Таким образом,
Регрессионный анализ позволяет установить степень влияния независимых величин на зависимую переменную.
При

помощи регрессионного анализа возможно решение задачи прогнозирования.
Уравнение регрессии выглядит следующим образом: Y=a+b*X
Прогнозные значения вычисляются путем подстановки в уравнение регрессии параметров значений объясняющих переменных
Используем пакет «Регрессия».
Слайд 132 вопрос занятия –
решение задач с помощью методов линейной регрессии

Слайд 14Подключение пакета анализа
Анализ данных в Microsoft Excel Microsoft Excel имеет большое число
статистических функций. Некоторые являются встроенными, некоторые доступны после установки пакета анализа.
Средства, включенные в пакет анализа данных, доступны через команду Сервис == Анализ данных. Если эта команда отсутствует в меню, в меню Сервис/Надстройки необходимо активировать пункт "Пакет анализа".
Пошаговый алгоритм есть здесь https://lumpics.ru/regression-analysis-in-excel/
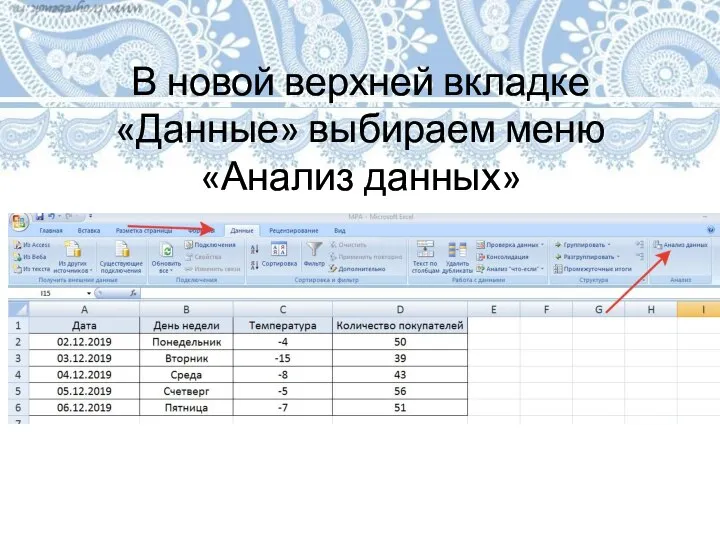
Слайд 16В новой верхней вкладке «Данные» выбираем меню «Анализ данных»
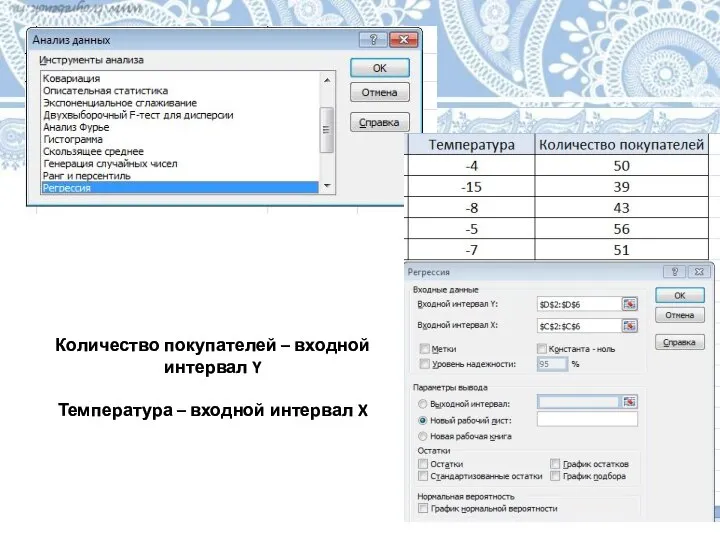
Слайд 17Количество покупателей – входной интервал Y
Температура – входной интервал X
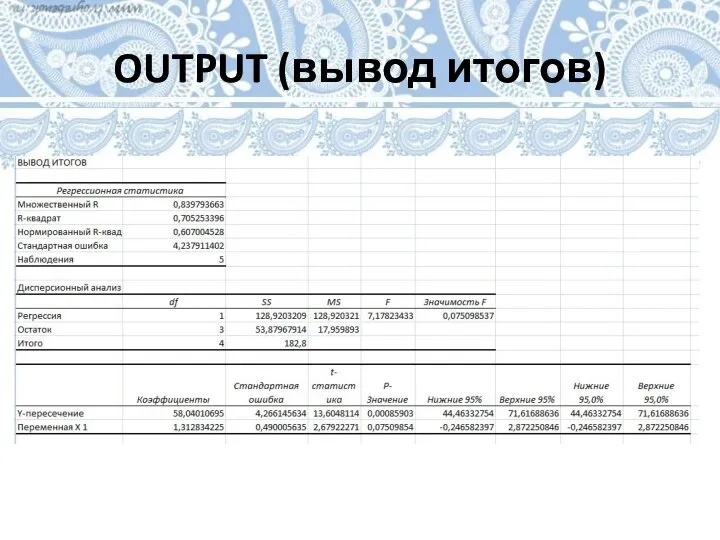
Слайд 19Разбор результатов анализа
1 шаг – установить наличие статистически значимой линейной связи между

переменными
Одним из основных показателей является R-квадрат. В нем указывается качество модели.
В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Следовательно, можно построить уравнение регрессии
Зависимость менее 0,5 является плохой. В этом случае уравнение регрессии построить нельзя. Анализ на этом заканчивается.
Слайд 20Разбор результатов анализа
2 шаг – доказать значимость линейной модели (дисперсионный анализ)
В данном
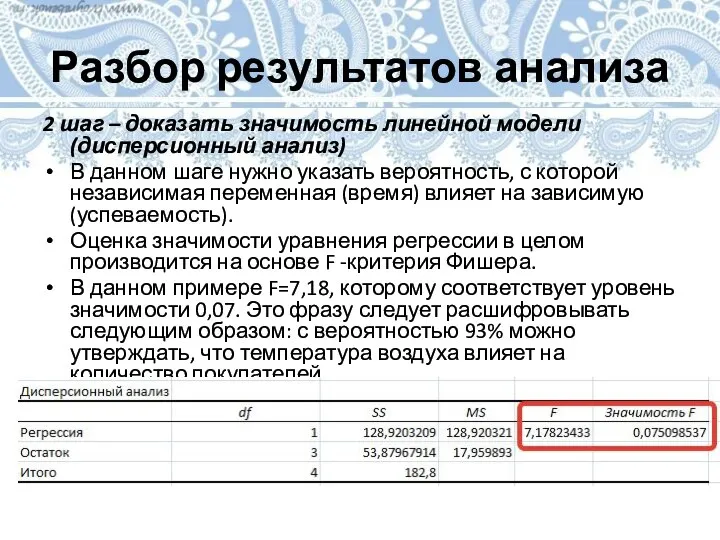
шаге нужно указать вероятность, с которой независимая переменная (время) влияет на зависимую (успеваемость).
Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера.
В данном примере F=7,18, которому соответствует уровень значимости 0,07. Это фразу следует расшифровывать следующим образом: с вероятностью 93% можно утверждать, что температура воздуха влияет на количество покупателей.
Слайд 21Разбор результатов анализа
3 шаг – составить уравнение регрессии, доказать значимость коэффициента и

свободного члена построенного уравнения.
Для построения модели линейной регрессии из данной таблицы используется коэффициент Y-пересечения.
Оценка его значимости проводится по t-критерию Стьюдента. В данном случае уровень значимости t-критерия Стьюдента меньше 0,001 (равен 0,0008), следовательно, можно говорить о статистической значимости коэффициента Y-пересечения.
В случае, если уровень значимости t-критерия Стьюдента (p-значение) меньше, чем 0,05, уравнение регрессии построить нельзя.
Слайд 22Разбор результатов анализа
3 шаг – составить уравнение регрессии, доказать значимость коэффициента и

свободного члена построенного уравнения.
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bX, где
X - независимая переменная,
Y – зависимая переменная (или переменная отклика). Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
a – свободный член (пересечение) линии оценки; это значение Y, когда Х=0,
b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем Х на одну единицу.
Уравнение регрессии в данном случае выглядит как:
Y (количество посетителей) = 58 + 1,3 * Х.
Слайд 23Построение предсказательной модели
Регрессионный анализ позволяет предсказать - на основе уравнения регрессии –
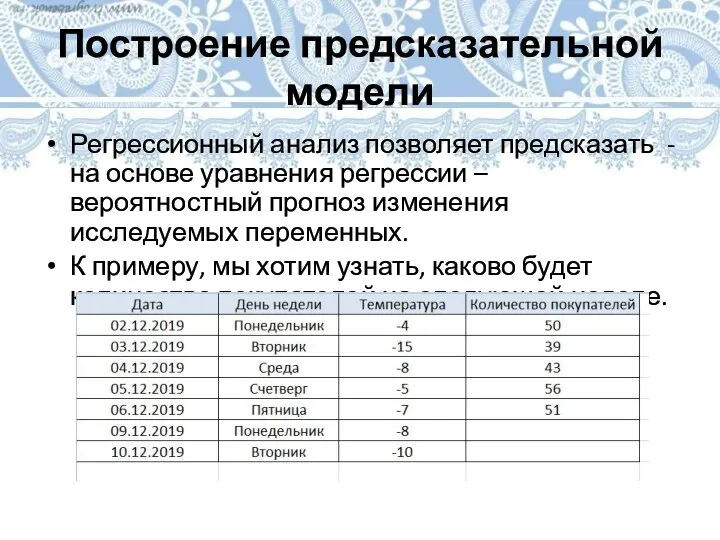
вероятностный прогноз изменения исследуемых переменных.
К примеру, мы хотим узнать, каково будет количество покупателей на следующей неделе.
Слайд 24Построение предсказательной модели
заложим вычисленное уравнение регрессии = 58 + 1,3 * Х
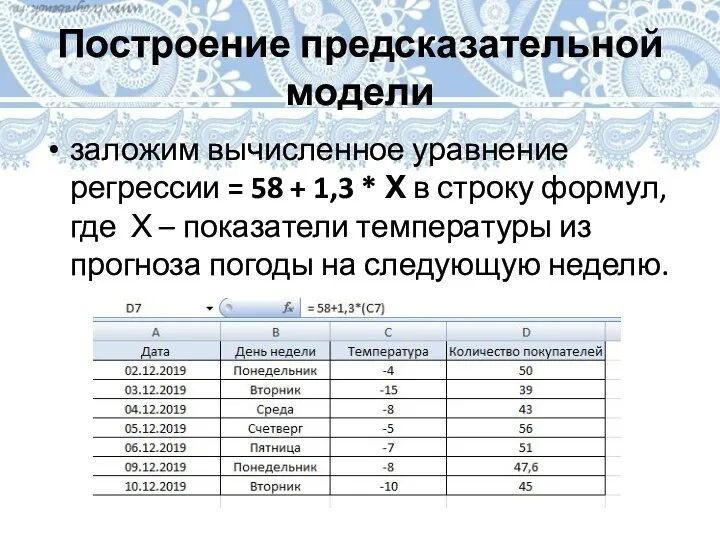
в строку формул, где Х – показатели температуры из прогноза погоды на следующую неделю.
Слайд 25Ответ задачи
Уравнение линейной регрессионной зависимости числа покупателей от температуры воздуха Y =

58 + 1,3* Х.
Прогноз числа покупателей для температуры -8 С равен 47,6 чел; для температуры -10 С равен 45 чел.
В целом можно говорить о температуры окружающей среды на количество покупателей в торговой точке.
Слайд 27Для каждой задачи необходимо выполнить 4 шага и записать ответ
установить наличие статистически

значимой линейной связи между переменными
доказать значимость линейной модели (дисперсионный анализ)
составить уравнение регрессии, доказать значимость коэффициента и свободного члена построенного уравнения
рассчитать прогнозные показатели
Слайд 28Задача 1
Исследователь пытается выявить взаимосвязь между количеством времени X, бесполезно потраченного студентами,
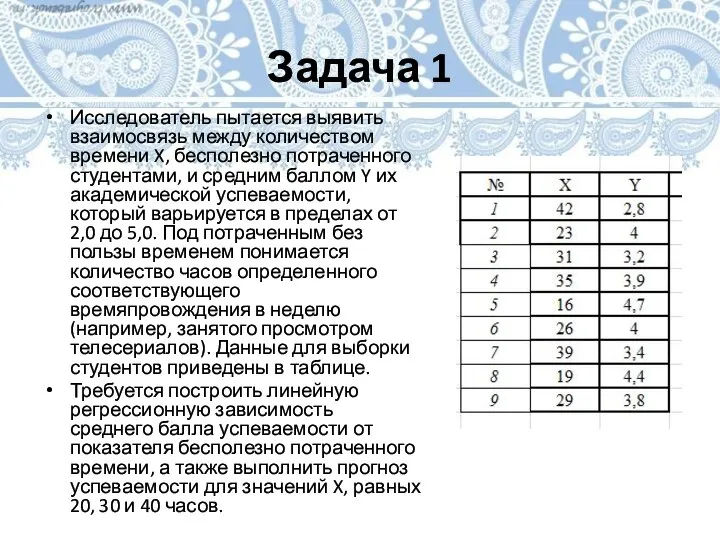
и средним баллом Y их академической успеваемости, который варьируется в пределах от 2,0 до 5,0. Под потраченным без пользы временем понимается количество часов определенного соответствующего времяпровождения в неделю (например, занятого просмотром телесериалов). Данные для выборки студентов приведены в таблице.
Требуется построить линейную регрессионную зависимость среднего балла успеваемости от показателя бесполезно потраченного времени, а также выполнить прогноз успеваемости для значений X, равных 20, 30 и 40 часов.
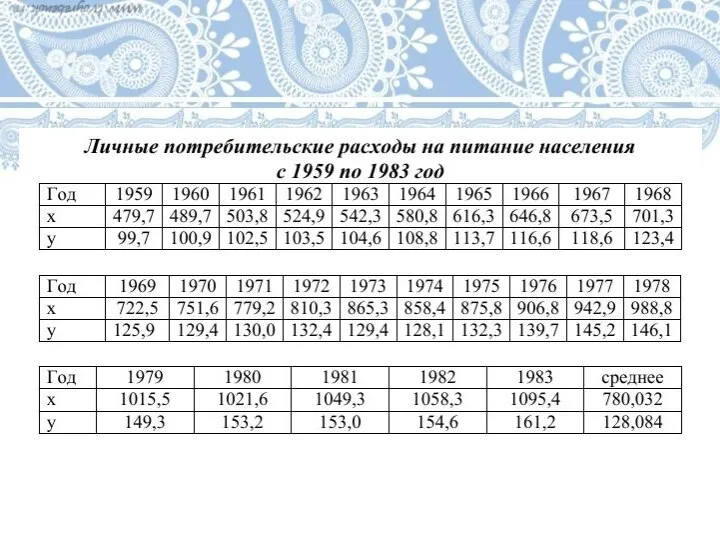
Слайд 29Задача 2
Исследователями были изучены данные о расходах потребителей на питание за 1959-1983

годы (данные на следующем слайде).
Требуется вычислить уравнение регрессии между расходами потребителя на питание (Y) и располагаемым личным доходом (X) по данным, приведенным для США за период с 1959 по 1983 год.
Исследователю хотелось бы предсказать расход на питание в 1984 году при личном доходе потребителя 1 239,3.
Слайд 31Задача 3
Проведено исследование, направленное на выявление взаимосвязи когнитивных и ценностно-мотивационных характеристик и

показателя успешности учебной деятельности студентов-экономистов по изучению компьютерных технологий. Использовались следующие психологические показатели, измеренные в баллах по шкале от 1 до 7. Показатель успешности учебной деятельности рассчитывался по специальной методике в шкале 20-80 (данные в отдельной таблице).
Требуется построить для успешности рассматриваемой деятельности оптимальную линейную регрессионную зависимость от психологических показателей.
Предсказать, насколько будет успешен Иван Иванович Иванов (испытуемый 19).
Слайд 32Задача 4 (не обязательно, возможно для зачета)
Проведены измерения черт характера и адаптивных

способностей у солдат срочной службы - новобранцев в космических войсках (данные в отдельной таблице).
Определить, какие черты характера соответствуют высоким адаптивным способностям (8 баллов), а какие – низким (6 баллов).
Слайд 33Выводы
Таким образом, в результате использования регрессионного анализа в пакете Microsoft Excel

мы:
построили уравнение регрессии;
установили форму зависимости и направление связи между переменными - положительная линейная регрессия, которая выражается в равномерном росте функции;
установили направление связи между переменными;
оценили качество полученной регрессионной прямой;
смогли увидеть отклонения расчетных данных от данных исходного набора;
предсказали будущие значения зависимой переменной.
Если функция регрессии определена, интерпретирована и обоснована, и оценка точности регрессионного анализа соответствует требованиям, можно считать, что построенная модель и прогнозные значения обладают достаточной надежностью.
Прогнозные значения, полученные таким способом, являются средними значениями, которые можно ожидать.





























 Число 10
Число 10 Цилиндр. 11 класс
Цилиндр. 11 класс Системы линейных алгебраических уравнений. Лекция 3а
Системы линейных алгебраических уравнений. Лекция 3а Математика и спорт
Математика и спорт Тригонометрия. Итоговое повторение
Тригонометрия. Итоговое повторение Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Квадратичная функция
Квадратичная функция Геометрические построения
Геометрические построения Третий признак равенства треугольников. Математический диктант
Третий признак равенства треугольников. Математический диктант Подготовка к диагностической работе. 5 класс
Подготовка к диагностической работе. 5 класс Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная В стране математики
В стране математики Модуль комплексного числа
Модуль комплексного числа Древняя Индия
Древняя Индия Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Презентация на тему Проценты в нашей жизни
Презентация на тему Проценты в нашей жизни  Презентация на тему Повторение курса начальной школы в 5-м классе
Презентация на тему Повторение курса начальной школы в 5-м классе  Задачи, обратные данной
Задачи, обратные данной Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3)
Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3) Пушкин и математика
Пушкин и математика 764fab9c-7974-40e4-8362-2c4469fed7e2
764fab9c-7974-40e4-8362-2c4469fed7e2 Сумма углов треугольника
Сумма углов треугольника Пространство и размерность
Пространство и размерность Логические задачи
Логические задачи Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Великая Отечественная война в числах
Великая Отечественная война в числах Прямая координата
Прямая координата Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение