Содержание
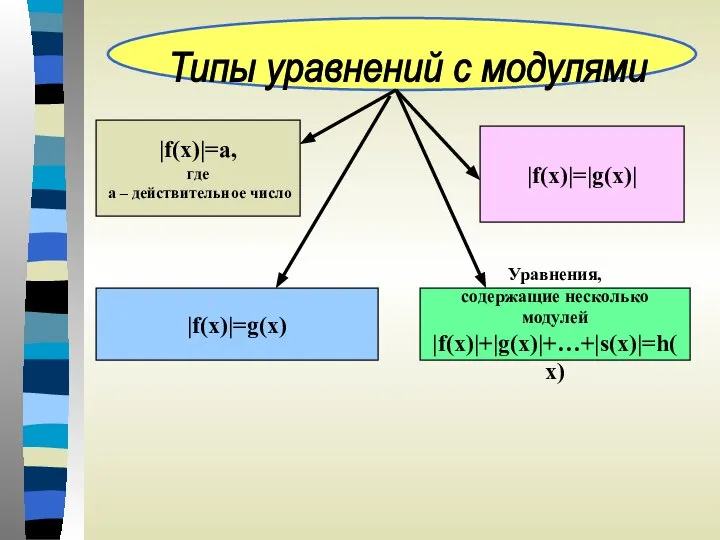
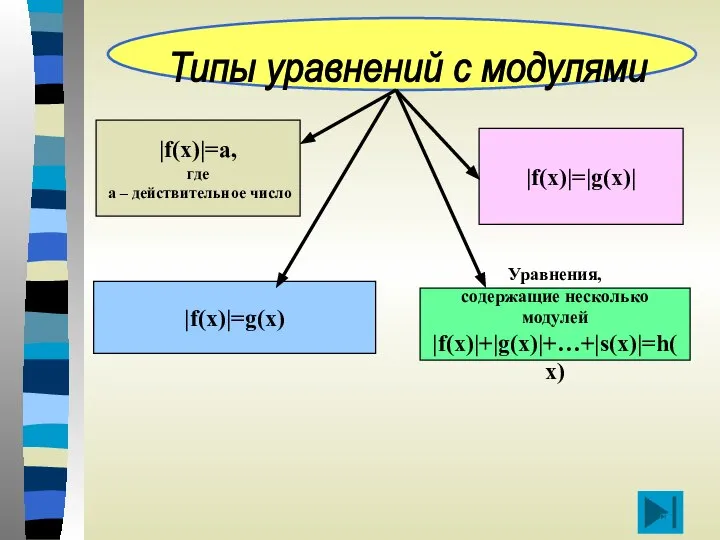
- 2. |f(x)|=a, где а – действительное число |f(x)|=g(x) |f(x)|=|g(x)| Уравнения, содержащие несколько модулей |f(x)|+|g(x)|+…+|s(x)|=h(x) Типы уравнений с
- 3. |f(x)|=a, где а – действительное число |f(x)|=g(x) |f(x)|=|g(x)| Уравнения, содержащие несколько модулей |f(x)|+|g(x)|+…+|s(x)|=h(x) Типы уравнений с
- 4. Решение уравнения |f(x)|=a 1) Если а > 0, то f(x)=a или f(x) = -a. 2) Если
- 5. Решение уравнений |f(x)|=|g(x)|. 1способ |f(x)|=|g(x)| f2(x) = g2(x) (f(x) - g(x)) (f(x) - g(x))=0 2 способ
- 6. Решение уравнений |f(x)|=g(x).
- 7. Решение уравнений, содержащих несколько модулей Находим значения переменной, при которых значения модулей равны 0. 2. Полученные
- 9. Скачать презентацию




 Анимированный плакат Цифры – прописи
Анимированный плакат Цифры – прописи 3_Equations_2
3_Equations_2 Вектори на площині. Завдання для самоперевірки знань
Вектори на площині. Завдання для самоперевірки знань Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс) Арифметические действия
Арифметические действия Основное тригонометрическое тождество и его следствия
Основное тригонометрическое тождество и его следствия ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Решение иррациональных неравенств
Решение иррациональных неравенств Множества и отношения
Множества и отношения Ряды. Сходимость рядов
Ряды. Сходимость рядов Презентация на тему Умножение и деление на 10 и 100
Презентация на тему Умножение и деление на 10 и 100  Операции над множествами
Операции над множествами Төзек күпкырлыклар
Төзек күпкырлыклар перпендикулярные прямые 7 класс
перпендикулярные прямые 7 класс Логика предикатов. Cостав математической логики
Логика предикатов. Cостав математической логики Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Общие уравнения прямой. Уравнение (формула)
Общие уравнения прямой. Уравнение (формула) Смежные углы
Смежные углы Вычитание с переходом через десяток
Вычитание с переходом через десяток Скалярное произведение векторов
Скалярное произведение векторов Второй признак равенства треугольников
Второй признак равенства треугольников Презентация на тему Мнимая единица
Презентация на тему Мнимая единица  Интерактивный тест. Готовимся к ОГЭ. 1 вариант, задание 2
Интерактивный тест. Готовимся к ОГЭ. 1 вариант, задание 2 Презентация на тему Простейшие вероятностные задачи
Презентация на тему Простейшие вероятностные задачи  Понятие функции
Понятие функции Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА
Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА