Слайд 22. Определители
Под определителем (детерминантом) понимают число, соответствующее квадратной матрице любого порядка и

вычисленное по определенным правилам.
Обозначают определитель матрицы А:
Δ Δ(А) |A| det A
Слайд 5Рассмотрим матрицу третьего порядка:

Слайд 6Минором Мij элемента аij матрицы А называется определитель, соответствующий матрице, полученной после

вычеркивания i-ой строки и j-го столбца в матрице А.
Слайд 7Аij=(-1)i+jMij
Алгебраическим дополнением Аij элемента аij , матрицы А называется минор этого элемента,

вычисленный по формуле:
Например:
Слайд 8Пример 2. Найти алгебраические дополнения элементов первой строки матрицы:
Решение:

Слайд 9Определителем третьего порядка называется число, равное сумме произведений элементов строки (столбца) на

их алгебраические дополнения:
Или:
Слайд 11Замечание
При вычислении определителя третьего порядка пользуются правилом Саррюса:
К определителю приписывают два

первых столбца: со знаком «+» берутся произведения трех элементов, стоящих на главной диагонали и на прямых, ей параллельной;
Со знаком «-» - произведения трех элементов, стоящих на побочной диагонали и прямых, ей параллельной.
Слайд 12
Например:
= 2·9·5 + 1·3·7 + 4·6·8 – 4·9·7 – 2·3·8 – 1·6·5

=
= 90 + 21 + 192 – 252 – 48 – 30 = –27
Слайд 13Этот же способ обычно называют «методом треугольника» и вычисления производят по следующей
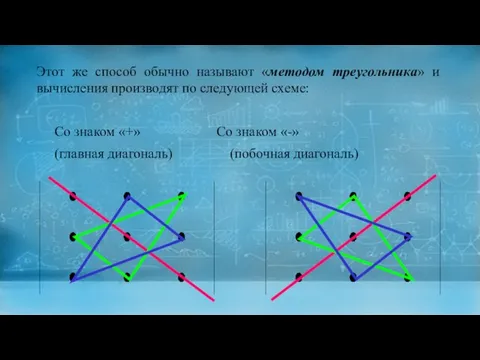
схеме:
Со знаком «+» Со знаком «-»
(главная диагональ) (побочная диагональ)
Слайд 14
Пример 4. Вычислить
Решение.
Δ = 3·6·(-2) + 1·1·0 +5·5·4 - 4·6·0 -

5·1·3 - 5·1·(-2) =
= -36 +100 - 15 +10 = 59.
Слайд 15Определителем п-го порядка называется число, равное сумме произведений элементов строки (столбца) на

их алгебраические дополнения:
Слайд 16Свойства определителей
1. Определитель матрицы А равен определителю транспонированной матрицы
det A = det

AТ
Таким образом, строки и столбцы определителя равноправны, все дальнейшие свойства справедливы как для строк, так и для столбцов определителя.
Слайд 172. Перестановка двух соседних строк (столбцов) изменит знак определителя на противоположный.
3. Формула

разложения определителя по любой строке (столбцу).
Определитель равен алгебраической сумме произведений элементов любой строки (столбца) на соответствующие алгебраические дополнения.
Слайд 184. Если две строки (столбца) определителя одинаковы, то определитель равен нулю.

Слайд 195. Если элементы некоторой строки (столбца) умножить на одно и то же

число k, то определитель умножится на это число. Другими словами, общий множитель элементов строки (столбца) можно вынести за знак определителя.
Слайд 206. Если элементы двух строк (столбцов) определителя пропорциональны, то он равен нулю.

Слайд 217. Если элементы некоторой строки (столбца) являются суммой двух слагаемых, то определитель

равен сумме двух определителей, соответствующие строки которых состоят из этих слагаемых:
8. Если элементы некоторой строки (столбца) равны нулю, то определитель равен нулю.
Слайд 229. Алгебраическая сумма произведений элементов некоторой строки (столбца) на алгебраические дополнения элементов

другой строки (столбца) равна нулю.
10. Определитель не изменится, если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца), умноженные на число k.
Слайд 23Доказательство.
Пусть,
Рассмотрим:

Слайд 24
Пример 5. Вычислить
Решение:
К первой строке прибавим третью, умноженную на (-4); ко

второй строке прибавим третью, умноженную на (-2); полученный определитель разложим по первому столбцу, тогда:
Слайд 26Далее к первой и третьей строкам прибавим вторую, умноженную на (-2) и

разложим по элементам первого столбца.
Получим:
Слайд 27
Пример 6. Вычислить
Решение.
Используем теорему Лапласа. Основные миноры образуем из третьей и

четвертой строк. Очевидно, что здесь только один минор второго порядка отличен от нуля, остальные равны нулю, дополнительный минор:
Слайд 29
Пример 7. Вычислить
Решение.
Преобразуем определитель так, чтобы все миноры второго порядка в

первых двух строках равнялись нулю. Прибавим к третьему столбцу первый, умноженный на (-4), к четвертому - второй, умноженный на (-2).




























 Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Доли. Устный счет
Доли. Устный счет Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Решение уравнений
Решение уравнений Признаки классификации статистической сводки
Признаки классификации статистической сводки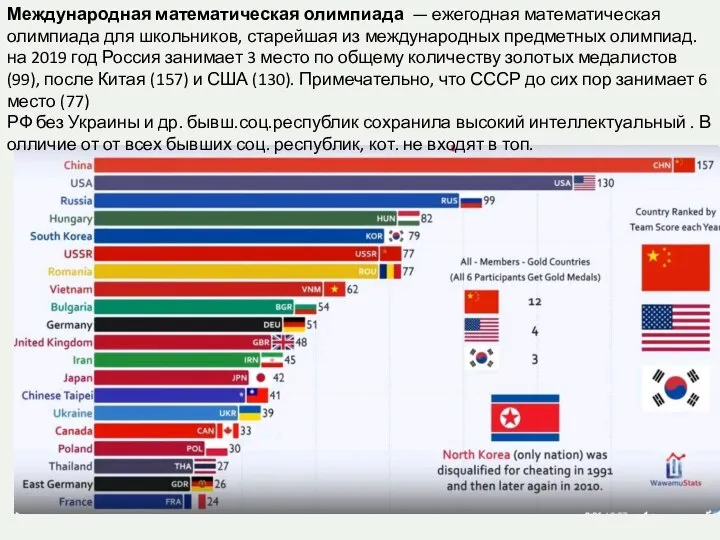 Международная математическая олимпиада
Международная математическая олимпиада Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Презентация на тему Математический КВН 8 класс
Презентация на тему Математический КВН 8 класс  Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Векторы. Действия с векторами
Векторы. Действия с векторами Вычитание и сложение чисел
Вычитание и сложение чисел Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Обработка многократных измерений
Обработка многократных измерений Запомни координаты. Игра
Запомни координаты. Игра Теорема Пифагора для пятиклассников
Теорема Пифагора для пятиклассников Приложения производной
Приложения производной Порядок элемента. Теорема Лагранжа
Порядок элемента. Теорема Лагранжа Теорія множин. Відношення
Теорія множин. Відношення Параллельные прямые. Решение задач
Параллельные прямые. Решение задач урок 1 и 2 (1)
урок 1 и 2 (1) Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Многоранники
Многоранники