Слайд 2 В общем случае линия пересечения двух поверхностей представляет собой пространственную кривую.

Линию пересечения поверхностей обычно строят по ее отдельным точкам, принадлежащих одновременно заданным поверхностям.
Форма линий пересечения зависит от формы и взаимного расположения поверхностей.
Прежде чем приступить к построению линии пересечения поверхностей, необходимо внимательно изучить условие,
т.е. выяснить какие поверхности пересекаются.
Слайд 3При решении задачи следует отметить в первую очередь характерные точки.
Это: 1.

Точки на крайних образующих;
2. Точки, делящие линию на видимую и невиди-мую часть;
3. Верхние и нижние точки и др.
Они позволяют определить границы линии пересечения, между которыми и следует определять промежуточные точки. Для нахождения промежуточных точек вводятся вспомогательные секущие посредники. Количество промежуточных точек должно быть достаточным для определения линии пересечения поверхностей. Построенные точки соединяют плавной кривой линией с учетом их видимости.
Слайд 4Чаще всего в качестве поверхностей-посредников при-меняют плоскости или сферы. Исходя из этого

различают следующие методы построения точек линии пересечения двух поверхностей:
— метод секущих плоскостей;
— метод секущих сфер.
Применение того или иного метода зависит от типа данных поверхностей и их взаимного расположения.
Слайд 5Построение линии пересечения двух поверхностей геометрических тел способом секущих плоскостей.
При использовании

метода секущих плоскостей вспомогательные плоскости выбираются таким образом, чтобы при их пересечении с заданными поверхностями получались простые сечения: прямые для линейных поверхностей или окружности для поверхностей вращения. Как правило, в качестве секущих плоскостей берутся либо плоскости уровня, либо проецирующие плоскости.
Слайд 6Метод секущих плоскостей
Пересечение поверхностей в общем случае – это вторая главная позиционная
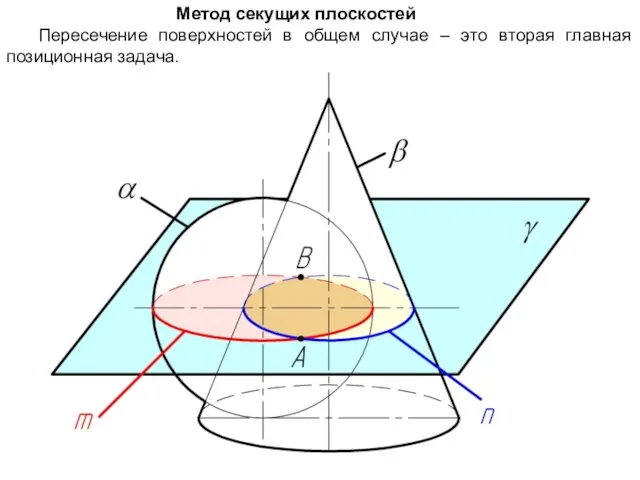
задача.
Слайд 7 Метод секущих плоскостей применяется, если оси пересекающихся поверхностей расположены параллельно.
Алгоритм решения:
1. Вводим

вспомогательную секущую плоскость γ (желательно проецирующую плоскость или плоскость уровня).
2. Определяем линии пересечения вспомогательной плоскости с каждой из поверхностей
α∩γ=m
β∩γ=n.
3. Находим точки, в которых пересекаются полученные линии
m ∩ n = A, B.
4. Определяем видимость линий пересечения и видимость поверхностей.
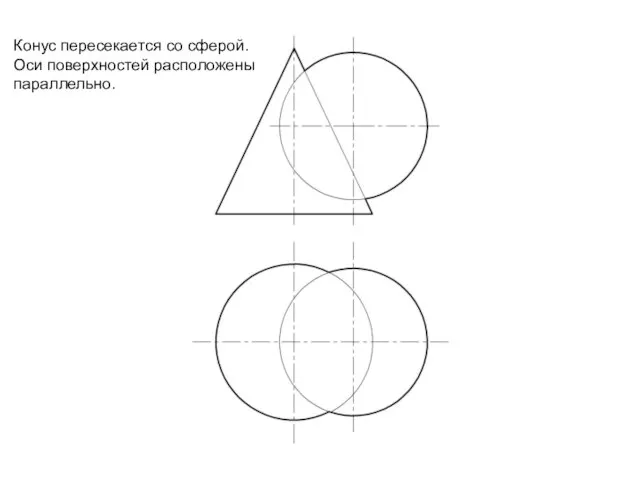
Слайд 8Конус пересекается со сферой.
Оси поверхностей расположены
параллельно.
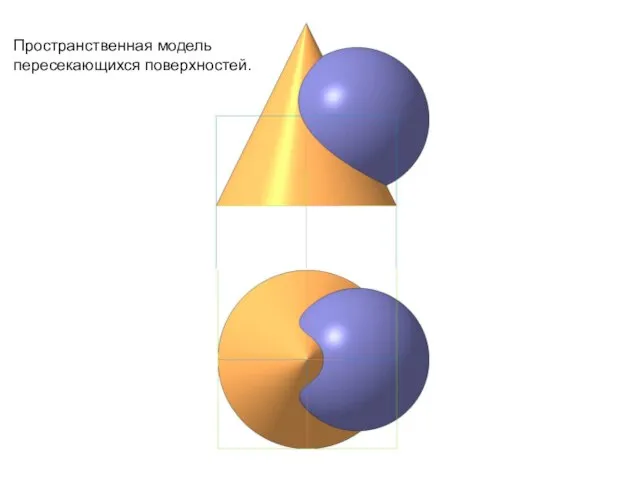
Слайд 9Пространственная модель
пересекающихся поверхностей.
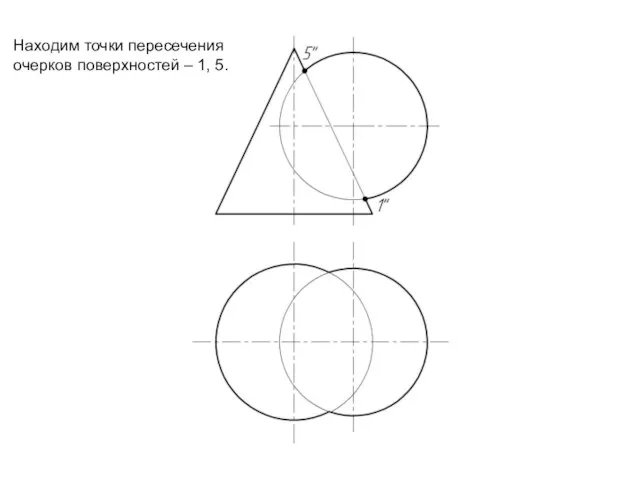
Слайд 10Находим точки пересечения
очерков поверхностей – 1, 5.
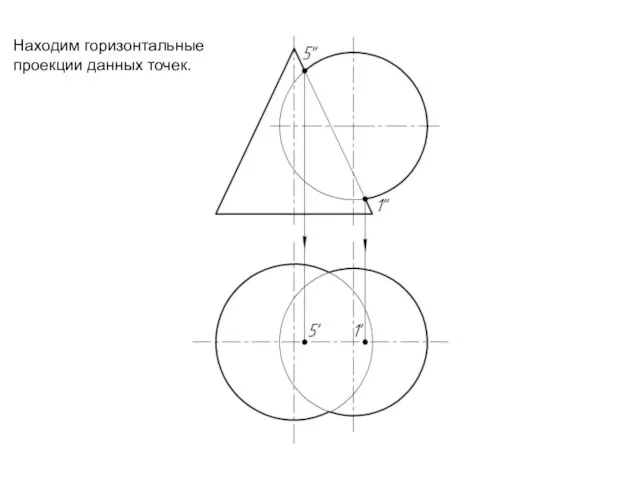
Слайд 11Находим горизонтальные
проекции данных точек.
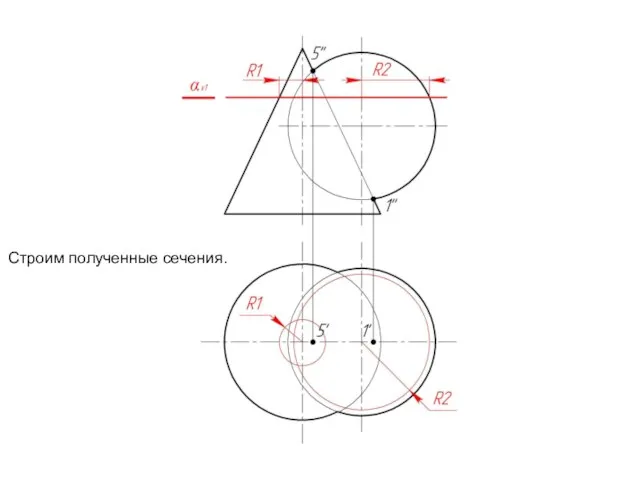
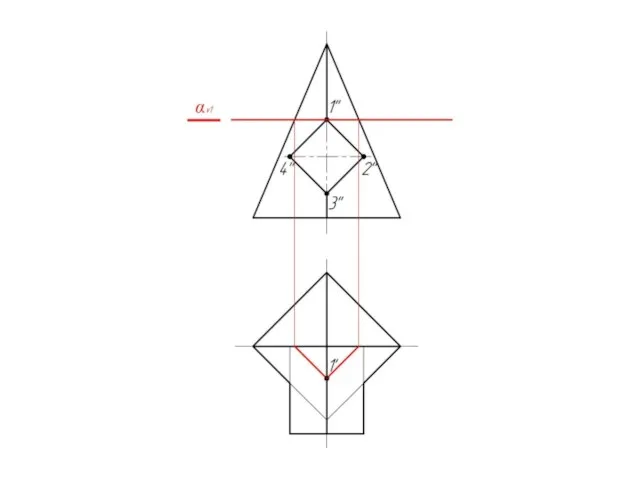
Слайд 12Проводим вспомогательную
cекущую плоскость αv1.
αv1 рассекает конус по
окружности радиуса R1,
а сферу –
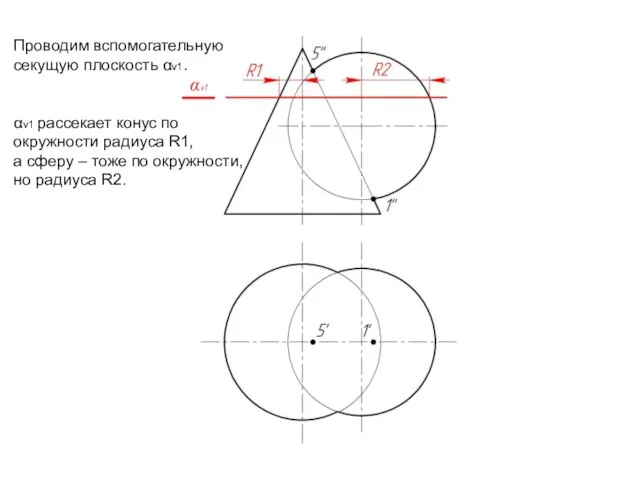
тоже по окружности,
но радиуса R2.
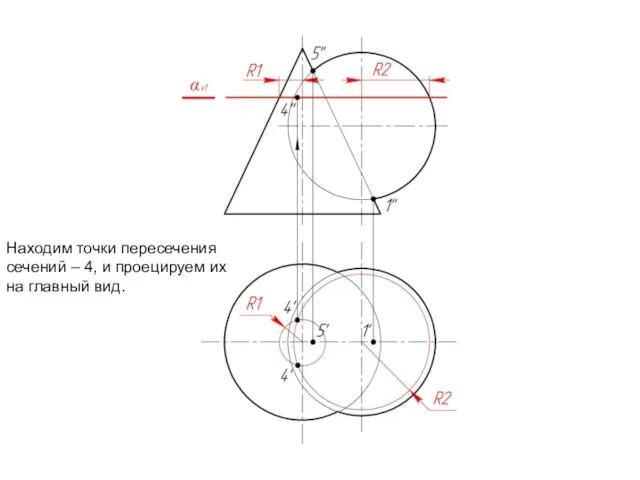
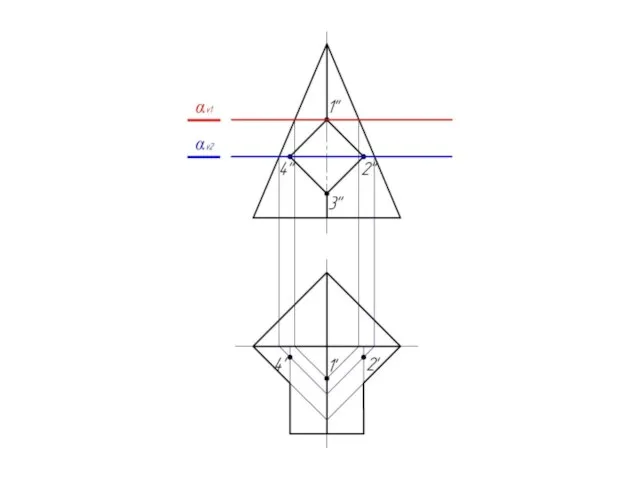
Слайд 14Находим точки пересечения
сечений – 4, и проецируем их
на главный вид.
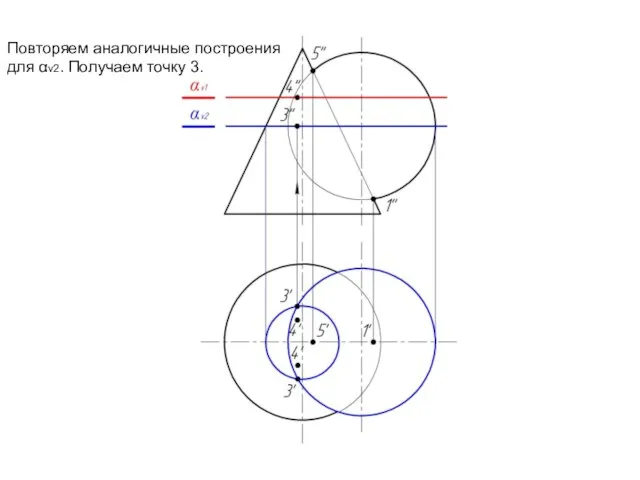
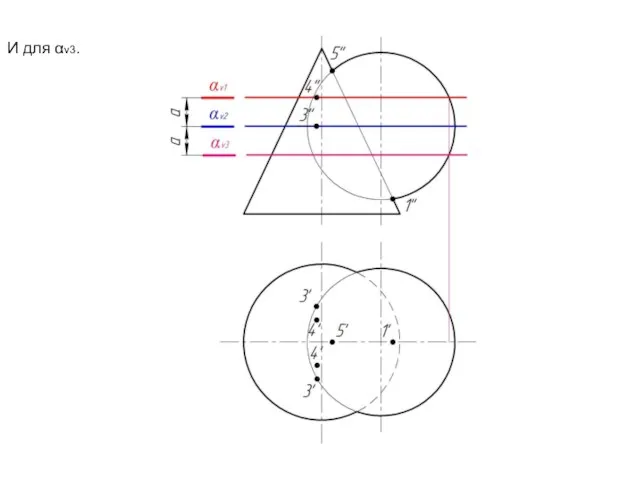
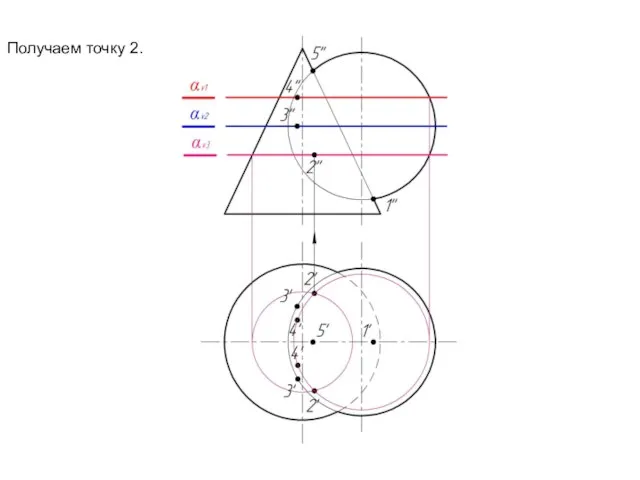
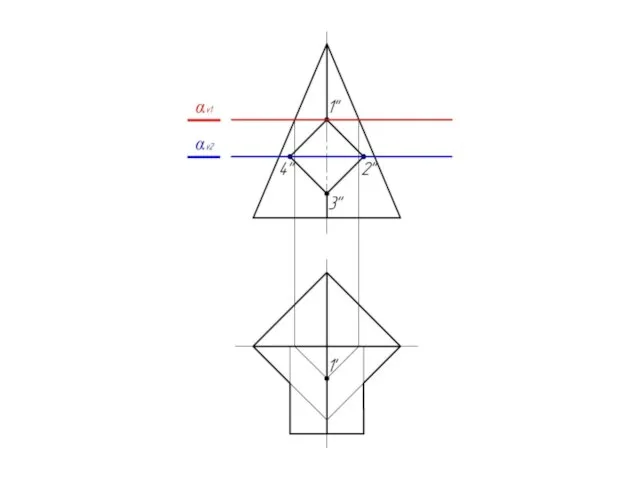
Слайд 15Повторяем аналогичные построения
для αv2. Получаем точку 3.
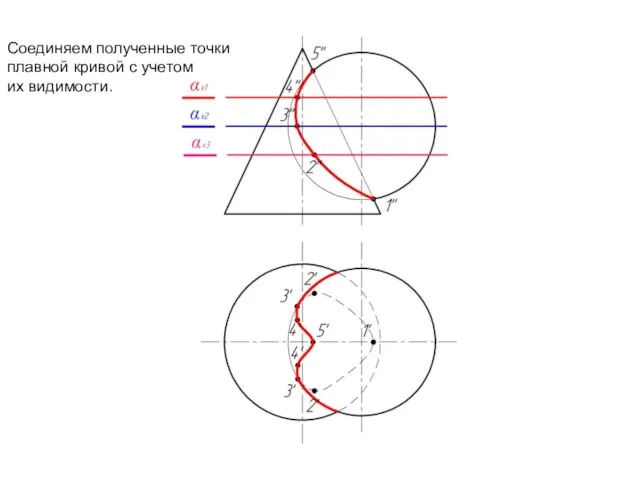
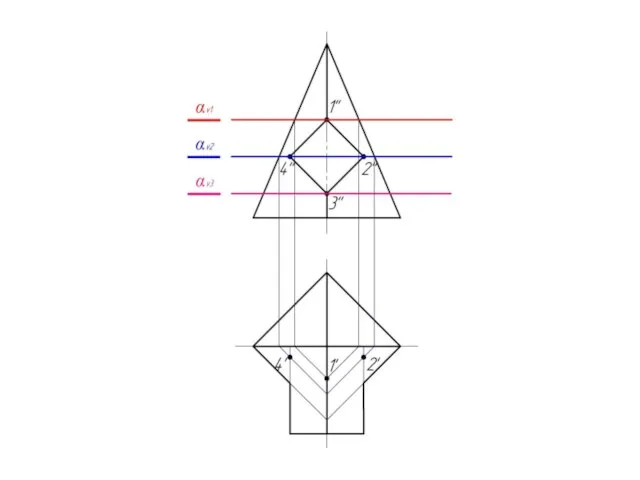
Слайд 18Соединяем полученные точки
плавной кривой с учетом
их видимости.
Слайд 19 Если одна из поверхностей является проецирующей, то решение задачи упрощается, т.к.

на одной из проекций линия пересечения совпадает с проекцией поверхности. И задача сводится к нахождению 2-й проекции линии.
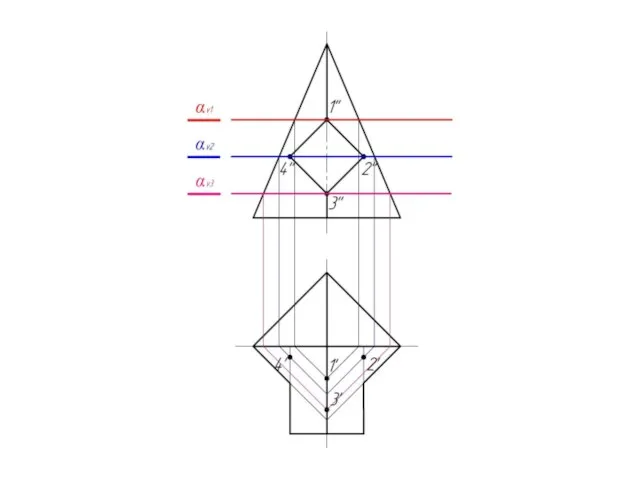
Слайд 21Пирамида пересекается с призмой.
Причем призма является в данном
случае проецирующей поверхностью.
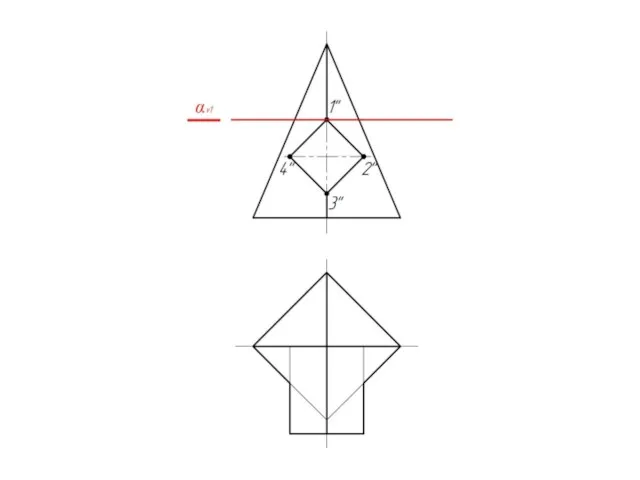
Следовательно на фронтальной
проекции
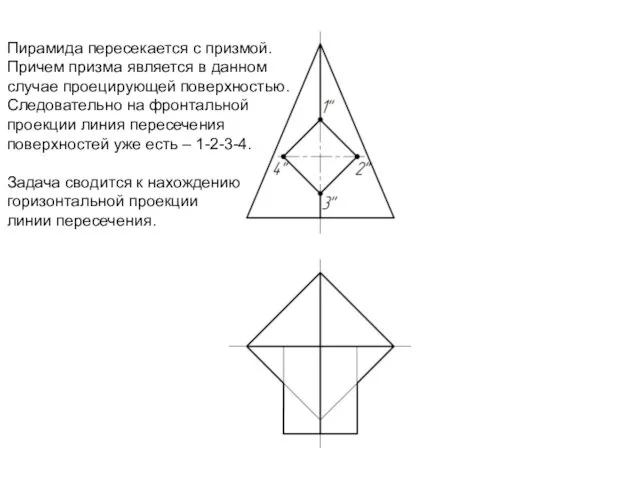
линия пересечения
поверхностей уже есть – 1-2-3-4.
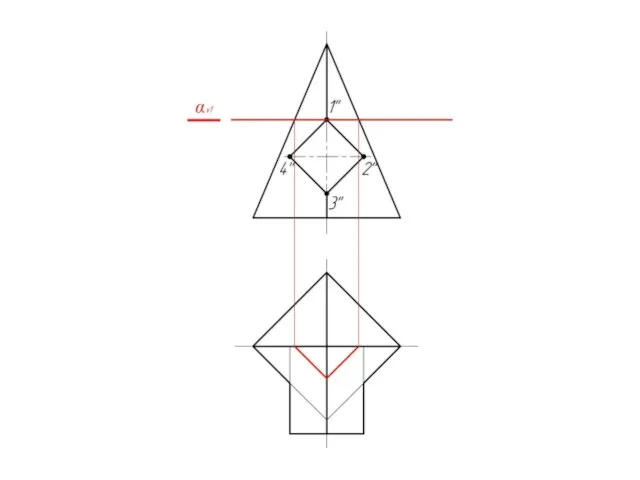
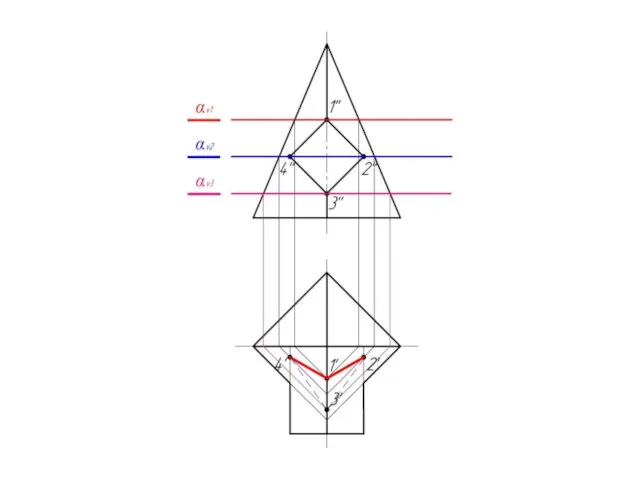
Задача сводится к нахождению
горизонтальной проекции
линии пересечения.















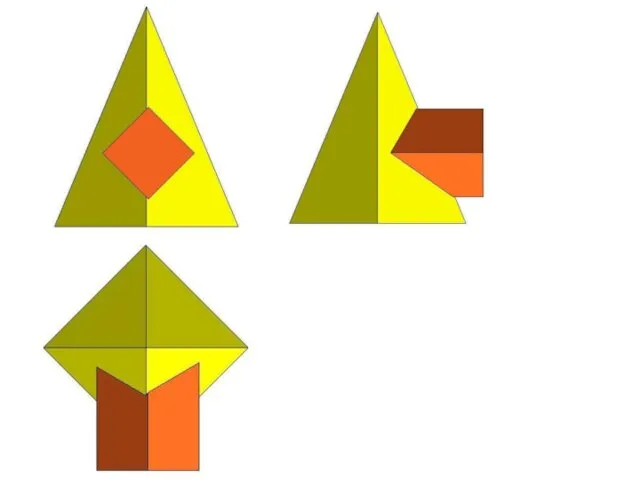

 Золотое сечение и симметрия
Золотое сечение и симметрия Простейшие логарифмические неравенства
Простейшие логарифмические неравенства Система географических координат
Система географических координат Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Применение игровых технологий на уроках математики в условиях внедрения ФГОС
Применение игровых технологий на уроках математики в условиях внедрения ФГОС Теорема Пифагора
Теорема Пифагора Основные тригонометрические тождества
Основные тригонометрические тождества Презентация на тему Свойства числовых неравенств
Презентация на тему Свойства числовых неравенств  Единицы измерения площадей
Единицы измерения площадей Вероятность события и ее свойства. Правила сложения и умножения вероятностей
Вероятность события и ее свойства. Правила сложения и умножения вероятностей Статистические оценки параметров распределения случайных величин по выборкам. Степенные средние
Статистические оценки параметров распределения случайных величин по выборкам. Степенные средние Дроби
Дроби ОГЭ 2020-21. Задание №8
ОГЭ 2020-21. Задание №8 Математический магазин
Математический магазин Размещения
Размещения Презентация на тему Сумма углов треугольника. Внешний угол треугольника
Презентация на тему Сумма углов треугольника. Внешний угол треугольника  Построение сечений многогранников
Построение сечений многогранников Веселый счет. Викторина
Веселый счет. Викторина Решение задач на нахождение зависимости между величинами используя графики
Решение задач на нахождение зависимости между величинами используя графики Трапеция
Трапеция Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Симметрия. Виды симметрии
Симметрия. Виды симметрии Решение задач, 1 класс
Решение задач, 1 класс Движение
Движение Презентация на тему Задачи на приведение к единице (3 класс)
Презентация на тему Задачи на приведение к единице (3 класс)  Путешествие в страну Математику
Путешествие в страну Математику Закрепление решения задач на приведение к единице
Закрепление решения задач на приведение к единице Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН
Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН