Моделирование при управлении рисками авиапредприятий

План
Введение: управление рисками и задачи моделирования
Построение модели
Байесовская вероятность
Принцип построения Байесовской сети
Использование сети для управления рисками АП
Вопросы для самопроверки

Руководящие документы
Руководство по управлению безопасностью полетов (РУБП) Международной организации гражданской авиации (ИКАО).
Воздушный кодекс и Федеральный закон Российской Федерации.
Правила разработки и применения систем управления безопасностью полетов воздушных судов, а также сбора и анализа данных о факторах опасности и риска, создающих угрозу безопасности полетов гражданских воздушных судов, хранения этих данных и обмена ими Министерства транспорта РФ и Федерального агентства воздушного транспорта.

Введение
Основные обстоятельства и определения
Риск – составное понятие, (учитывающее как вероятность, так и ущерб).
Нулевой уровень риска невозможен
Уровень риска меняется со временем даже в отсутствие событий риска и связан с убылью ресурса
События риска непредсказуемы, приводят к скачкообразному изменению ресурса и требуют специальных мер по его восстановлению до штатного уровня
В чем состоит управление рисками?
Управление рисками АП состоит в объективном, (не зависящем от мнения конкретного руководителя), обосновании характера и объема мер, необходимых для достижения заданного (штатного) уровня риска
Эта задача может быть решена посредством моделирования

Модель
Что такое модель, зачем нужна и как пользоваться
Модель – математическое уравнение или функциональная зависимость, отражающие реальные процессы, содержащие измеряемые параметры. Модель используется для расчета величины целевого параметра по заданным остальным.
Выбор параметров модели и связанные с этим проблемы
Заданные параметры – измеряются непосредственно или вычисляются, в т.ч. путем расчета средних значений или вероятностей. Для малой выборки аппарат классической теории вероятностей непригоден.
Необходимость статистики на отдельном АП и в целом по отрасли
Для определения вероятностей необходимо как можно больше однородных данных.
Объект моделирования
Изменение уровня риска со временем (или расход ресурса, связанный с эксплуатацией ВС)
Удобно привязать статистику всех событий (ЛЭ, АН, ТО, АэП) к каждому ВС для данного АП
Уровень риска, характеризующий АП, может быть определен на основе уровней риска для каждого ВС

Построение модели
Ресурс Rs каждого ВС за время от начала эксплуатации ВС до любой из предусмотренных регламентированных работ по восстановлению ресурса меняется от Rs0 до некоторого Rsмин (износ)
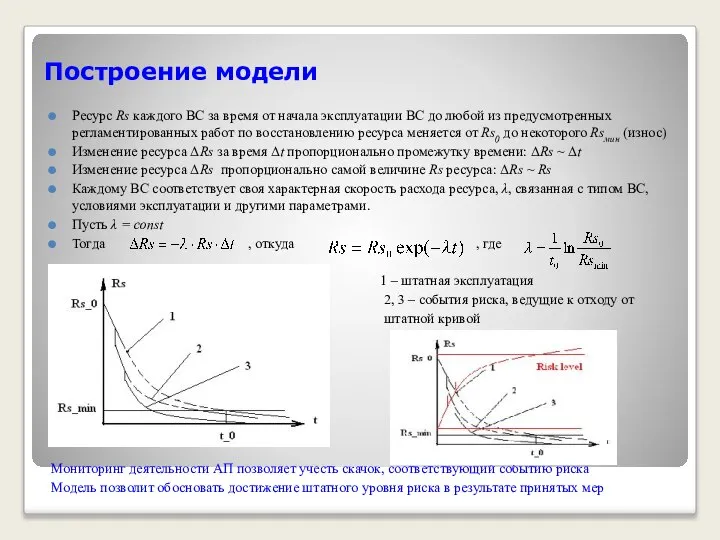
Изменение ресурса ΔRs за время Δt пропорционально промежутку времени: ΔRs ~ Δt
Изменение ресурса ΔRs пропорционально самой величине Rs ресурса: ΔRs ~ Rs
Каждому ВС соответствует своя характерная скорость расхода ресурса, λ, связанная с типом ВС, условиями эксплуатации и другими параметрами.
Пусть λ = const
Тогда , откуда , где
1 – штатная эксплуатация
2, 3 – события риска, ведущие к отходу от
штатной кривой
Мониторинг деятельности АП позволяет учесть скачок, соответствующий событию риска
Модель позволит обосновать достижение штатного уровня риска в результате принятых мер

Байесовская вероятность
Событие риска привело к скачку уровня риска. Для возвращения на штатный уровень необходимо:
1 – определить величину скачка риска (вероятность и ущерб)
2 – определить характер компенсирующих мероприятий (проверки и учения)
3 – обосновать количество необходимых мероприятий (модель)
Вероятность события риска зависит от большого числа факторов и очень мала по величине ? классическая теория вероятностей (КТВ) неприменима.
КТВ основана на существовании вероятности события независимо от данных опыта
Пример с бросанием монеты: изменение уверенности в исходе в зависимости от характера предшествовавшей серии
Байесовская ТВ предлагает узнать вероятность события по данным опыта
Пример с казино: как оценить возможность выигрыша
В результате анализа данных выдвигается гипотеза о том, чему равна вероятность события, и вычисляется вероятность того, что эта гипотеза истинна.
Пример с шарами: оценка вероятности может быть ошибочной, но без нее еще хуже

Формула Байеса
Известна формула Байеса
Вероятность события А, определяемая с помощью набора событий В, равна априорной вероятности А, умноженной на условную вероятность каждого из событий В (условие – А имеет априорную вероятность), деленную на сумму вероятностей всех событий В при всех возможных А.
Все подробности можно при необходимости узнать у специалистов
Для работы важно понимать:
р(А) - «априори» - исходная вероятность величины ресурса (или уровня риска). Она берется в соответствии с кривой, задаваемой моделью.
Условные вероятности р(В|А) – назначаются
из локальной статистики;
из экспертной оценки;
заданы произвольно.
Сумма вероятностей вычисляется известными математическими методами.
Формула Байеса позволяет найти вероятность того, что «априори» имеет место при учете событий риска. Это даст возможность вычислить величину «скачка» на графике.

Что это значит
Выбираем «априори» - вероятность уровня риска до того, как событие риска имело место (с использованием графика).
Задаем вероятности отдельных событий или действий, сопровождающих событие риска, например, генерирующих факторов.
Выполняем расчет по формуле Байеса и получаем новое – апостериорное – значение вероятности уровня риска.
Наступившее событие риска УВЕЛИЧИВАЕТ Байесовскую вероятность уровня риска.
Это позволяет вычислить величину скачка, представленного на графике.

Байесовские сети
Набор генерирующих факторов события риска следует упорядочить, установив наличие между ними причинно-следственных связей.
Тогда их можно представить в виде ориентированного графа – т.н. Байесовской сети.
Каждой его вершине сопоставляется n-значная переменная (фактор), а ребра обозначают причинно-следственные связи между соединенными узлами. При этом сила таких связей, т.е. зависимостей между переменными, будет количественно выражаться в виде условных вероятностей, сопоставленных каждой из переменных. Основной идеей построения сети является разложение сложной системы на простые элементы.
Все подробности можно при необходимости узнать у специалистов
Параметры модели рассчитываются с помощью Байесовской сети, построенной для данного АП. Структура сети должна отражать структуру состояния рисков. Проблемы, связанные с построением, настройкой и использованием сети, требуют специальных знаний или участия IT-специалиста. Задача руководителя АП или ответственного по управлению рисками – ясно понимать смысл и логику ее построения и участвовать в усовершенствовании сети, делая ее наиболее пригодной для своего АП.
Известны существующие программные системы («MSBN», Microsoft и «Hugin», Hugin AIS), позволяющие создавать необходимые байесовские сети.

Использование сети для управления уровнем риска
Произошло событие риска, которое не удалось предотвратить мерами по управлению безопасностью полетов.
Ваши действия:
1. Определить априорную вероятность уровня риска (до события риска) и рассчитать ее апостериорную вероятность (после события риска) с помощью Байесовской сети, построенной для данного АП. Найти их разность.
2. Определить характер компенсирующих мероприятий в соответствии с профессиональными требованиями (например, отработка действий экипажа на тренажере).
3. Провести контрольную проверку. Выбрать полученную в п.1 апостериорную вероятность в качестве априорной и рассчитать новую апостериорную вероятность с помощью Байесовской сети, построенной для данного АП. Найти новую разность между вероятностями.
4. Если величина новой разности превосходит предыдущую, то вероятность события риска вернулась к исходному значению.
5. Если новая разность не компенсирует предыдущую, следует продолжить компенсирующие мероприятия.
6. Вернуться на пункт 3.