Содержание
- 2. (an ): -17; -20; -23; -26;-29;-32;... (cn ): 1; 5; 25; 100; 400; 2000. (xn): 56;
- 3. (an):-17;-20;-23;-26;-29;-32;... d-? a10 - ? S15 - ? d= -3; a10= - 44; S15= -570
- 4. (xn): 56; -28; 14; -7; 3,5; ... q-? x8 - ?
- 5. В январе – 106 изделий В каждый следующий месяц - на 3 изделия больше, чем в
- 6. За 100 000 рублей 1 копейку 2 копейки 4 копейки 8 копеек 3 000 000 руб.
- 7. S30=1 + 2+4 +8+16 +...+ 229 1; 2; 4; 8; 16;...; 229 - геометрическая прогрессия n
- 8. Формулы суммы членов конечной геометрической прогрессии
- 9. (bn)= b1; b2; b3;…; bn- геометрическая прогрессия. Sn= b1+ b2+ b3+…+ bn qSn=b1q+b2q+b3q+…+bn-1q+bnq · q qSn-
- 10. Если q=1, то Sn= n∙b1 ?
- 11. № 1. (bn) - геометрическая прогрессия. b1= -32, b2= -16 Найти: S6 Решение: Ответ: S6= -
- 12. № 2. (bn)- геометрическая прогрессия. q=3, S4=560 Найти: b1 Решение: Ответ: b1=14
- 13. В классе: № 870(1,3,5), 872, 874, 876 Домашнее задание: § 25, вопросы, № 871(1,2), 873
- 15. Скачать презентацию


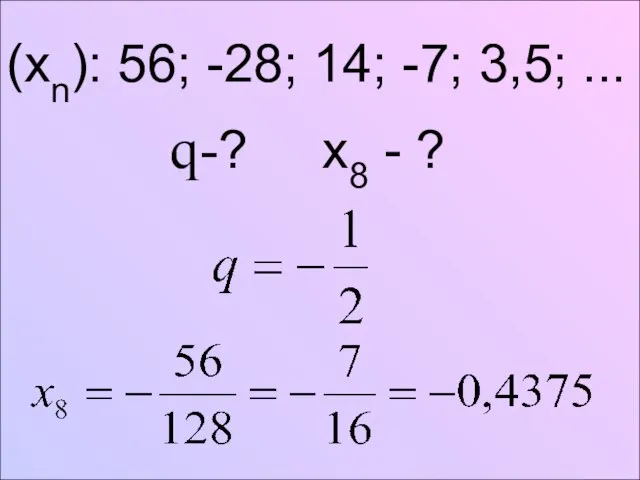









 Квадратная матрица
Квадратная матрица Задачи с обыкновенными дробями
Задачи с обыкновенными дробями Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Вычислите логарифм. Практическая работа
Вычислите логарифм. Практическая работа Математическое моделирование
Математическое моделирование Равенство векторов
Равенство векторов Міра. Однозначні, багатозначні міри
Міра. Однозначні, багатозначні міри Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Расчетно-графическая работа
Расчетно-графическая работа Случаи вычитания 11-
Случаи вычитания 11- Тела вращения. Цилиндр
Тела вращения. Цилиндр Математика в игре
Математика в игре Интеграл. Что называют криволинейной
Интеграл. Что называют криволинейной Одночлен и его стандартный вид
Одночлен и его стандартный вид Исследование функций
Исследование функций Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Величины. Объём
Величины. Объём Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.)
Алгебра 10кл - Презентация к уроку 1 (Самойлова Г. А.) kombinatorika_lektsia
kombinatorika_lektsia Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)
Сложение и вычитание вида ± 1, ± 2, ± 3 (1 класс)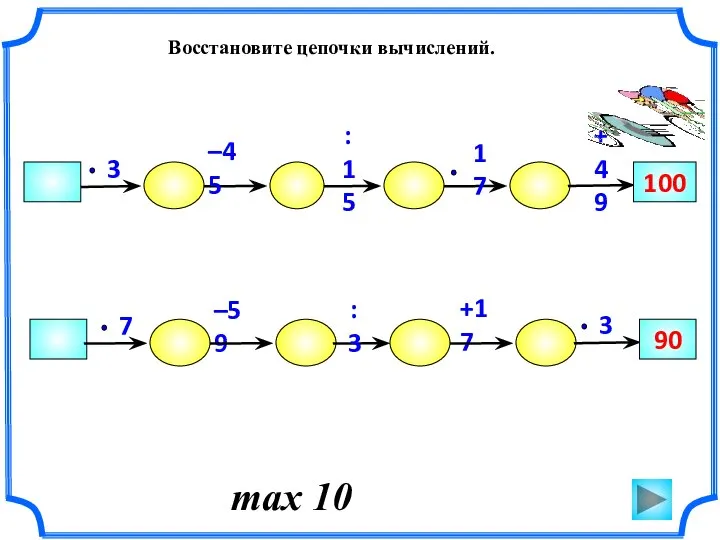 Дроби. Числитель дроби
Дроби. Числитель дроби Квадратные уравнения
Квадратные уравнения Периметр, площадь, объём
Периметр, площадь, объём Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Бесконечность величин
Бесконечность величин Умножение величины на число
Умножение величины на число Угол между векторами
Угол между векторами