Содержание
- 2. ТЕМА УРОКА Нахождение наибольшего и наименьшего значений функции « Дорогу осилит идущий, а математику — мыслящий»
- 3. Вот предо мной кривая: абсциссы – это даты; И следует запомнить, что деньги – ординаты. Когда
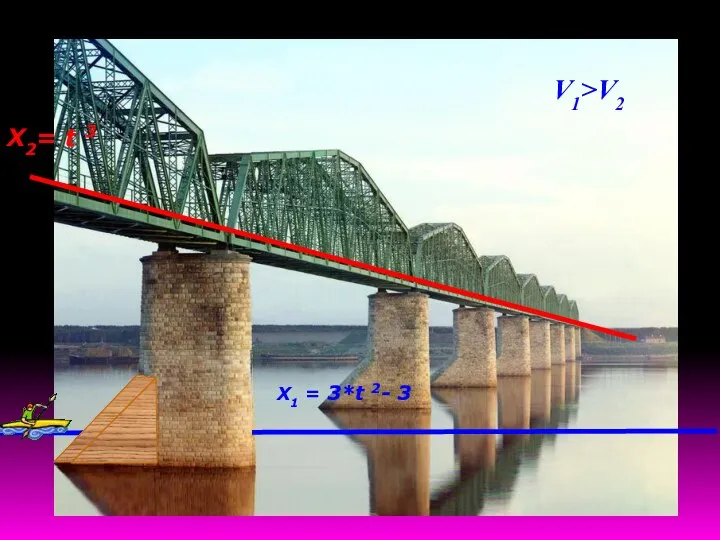
- 4. Х2= t 3 Х1 = 3*t 2- 3
- 6. Почему же произошла катастрофа?
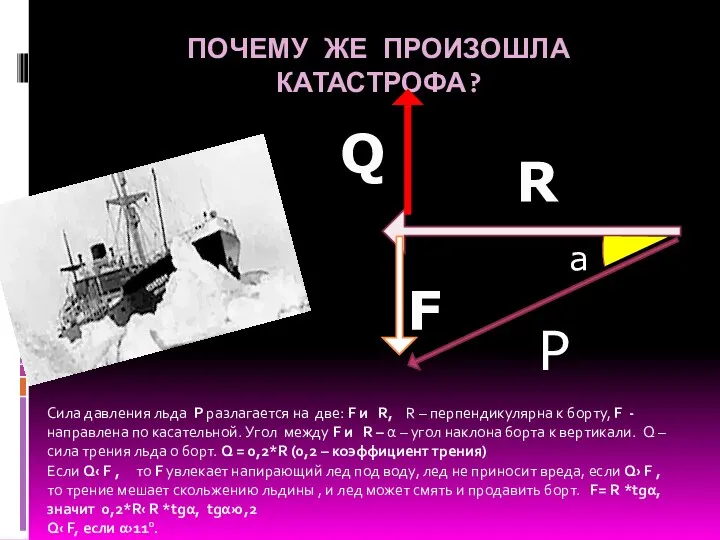
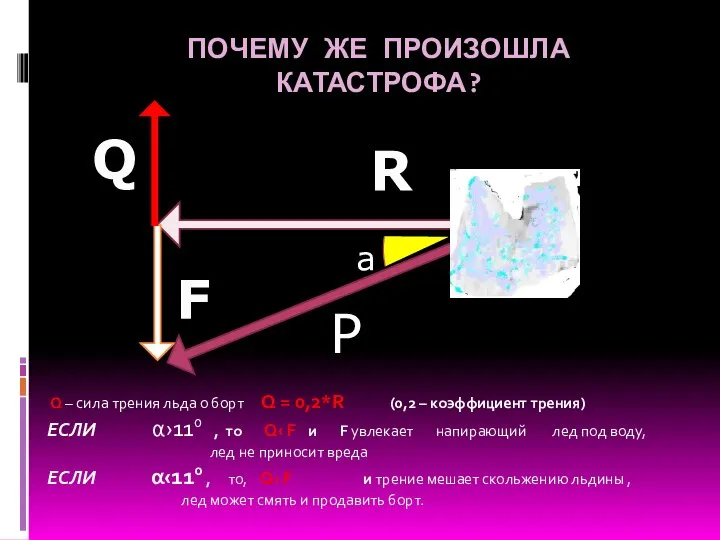
- 7. ПОЧЕМУ ЖЕ ПРОИЗОШЛА КАТАСТРОФА? Сила давления льда P разлагается на две: F и R, R –
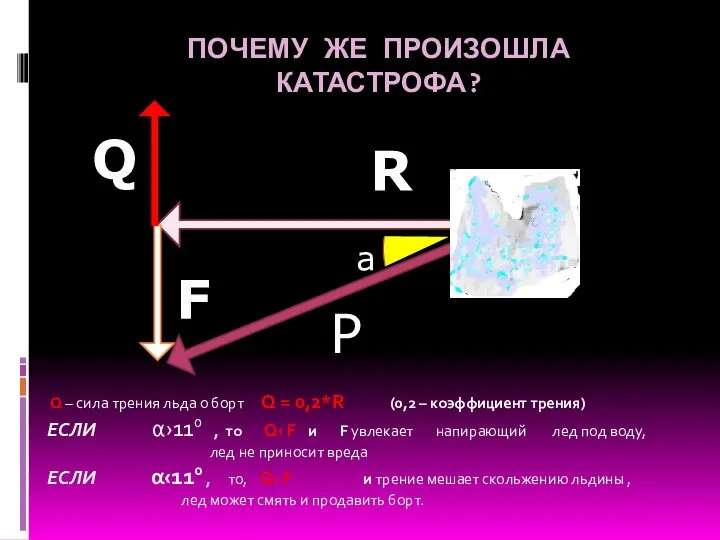
- 8. ПОЧЕМУ ЖЕ ПРОИЗОШЛА КАТАСТРОФА? Q – сила трения льда о борт Q = 0,2*R (0,2 –
- 9. ПОЧЕМУ ЖЕ ПРОИЗОШЛА КАТАСТРОФА? Q – сила трения льда о борт Q = 0,2*R (0,2 –
- 10. ЗАДАЧИ НА ОПТИМИЗАЦИЮ «Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей
- 11. Площади равны « А вместимость ?»
- 12. ЗАДАЧИ НА ОПТИМИЗАЦИЮ Алгоритм решения: ? Составить математическую модель задачи; ? Ввести переменную (Х), через которую
- 13. Пусть имеется квадрат со стороной 12 дм, из которого надо изготовить коробку наибольшей вместимости. Обозначим сторону
- 14. по рассказу Л.Н. Толстого «Много ли человеку земли нужно» Я - Пахом! Ух! 40 км прошёл.
- 15. Задача ДИДОНЫ
- 16. Домашнее задание Попробуйте самостоятельно доказать, что площадь занятая Дидоной ( в форме полукруга), больше чем площадь
- 17. производная - ПРОВЕРКА ЗНАНИЙ
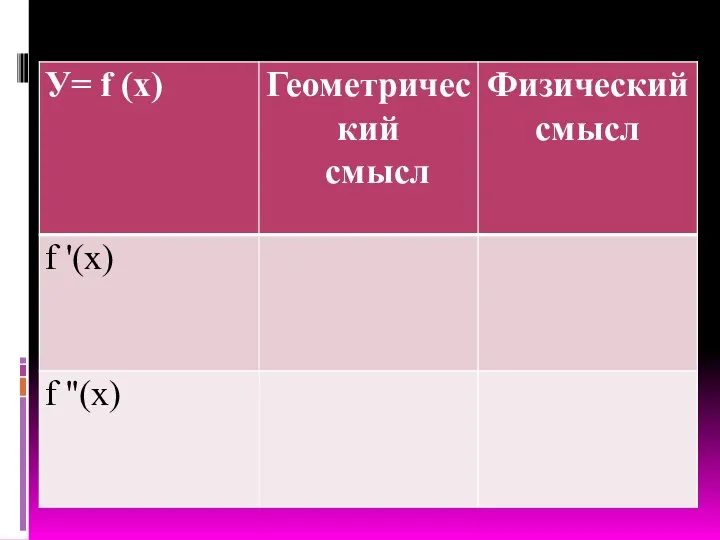
- 18. Математический диктант Математический диктант 1 1 вариант 2 вариант В чем сущность физического смысла производной? а)скорость;
- 20. Скачать презентацию












 Презентация на тему Свойства степени с целым показателем (8 класс)
Презентация на тему Свойства степени с целым показателем (8 класс)  Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер
Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора Иоганн Кеплер Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Диагностика уровня сформированности предметных умений и УУД. (1 класс)
Диагностика уровня сформированности предметных умений и УУД. (1 класс) Арифметические операции в разных системах счисления
Арифметические операции в разных системах счисления Группировки в историческом исследовании. (Лекция 2)
Группировки в историческом исследовании. (Лекция 2) Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс
Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс Понятие ”тетраэдр”
Понятие ”тетраэдр” Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Метод интервалов. Решаем неравенства!
Метод интервалов. Решаем неравенства! Таблица умножения с Лунтиком
Таблица умножения с Лунтиком Играем и считаем
Играем и считаем Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Математическое моделирование. Линейное программирование
Математическое моделирование. Линейное программирование Микрокалькулятор
Микрокалькулятор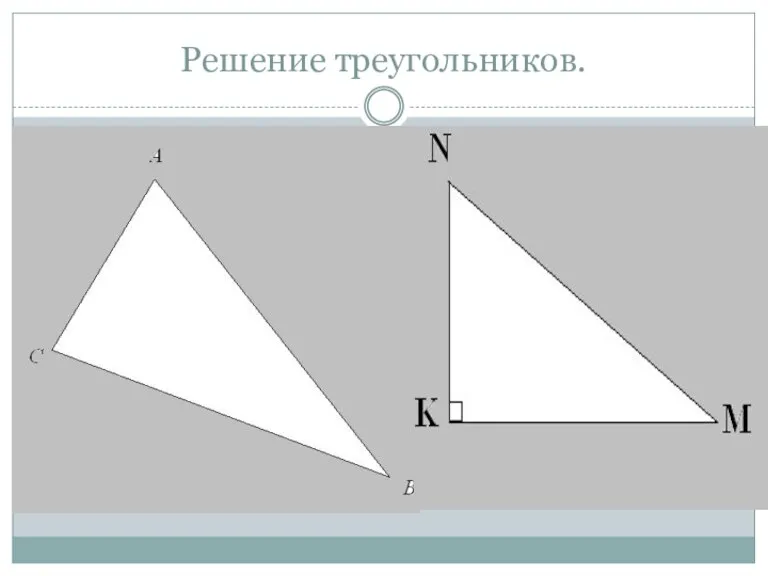 Решение треугольников
Решение треугольников Презентация на тему ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ
Презентация на тему ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ  Компьютерное решение задач по теме Арифметическая прогрессия
Компьютерное решение задач по теме Арифметическая прогрессия Деление дробей
Деление дробей Способ группировки
Способ группировки Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Число и цифра 5
Число и цифра 5 Задачи В Детском мире
Задачи В Детском мире Математика «Сравнение трехзначных чисел» 3 класс ОС «Школа 2100» Загатина А.О.
Математика «Сравнение трехзначных чисел» 3 класс ОС «Школа 2100» Загатина А.О. Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Трапеция. Основание
Трапеция. Основание Сложение и вычитание смешанных чисел. Графический диктант
Сложение и вычитание смешанных чисел. Графический диктант