Обработка экспериментальных данных. Описательная статистика: основные понятия

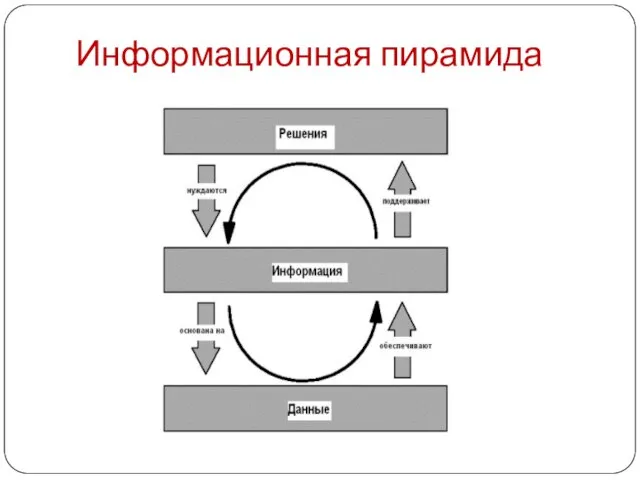
Информационная пирамида

Методы анализа данных
Статистические:
Дескриптивный анализ.
Анализ природы данных (проверка гипотез стационарности, нормальности, однородности, оценка вида функции распределения).
Анализ связей (корреляционный и регрессионный анализ, факторный анализ, дисперсионный анализ).
Многомерный статистический анализ .
Кибернетические:
Методы классификации.
Кластерный анализ.
Искусственные нейронные сети (распознавание, прогноз).
Деревья решений.
Методы ближайшего соседа и k-ближайшего соседа
Системы обработки экспертных знаний.

Генеральная и выборочная совокупности
Генеральная совокупность - вся совокупность изучаемых объектов, интересующая исследователя.
Выборка - часть генеральной совокупности, определенным способом отобранная с целью исследования и получения выводов о свойствах и характеристиках генеральной совокупности.

1. Номинальная шкала
2. Порядковая шкала
3. Интервальная шкала
4. Относительная шкала
5. Дихотомическая шкала
Виды шкал

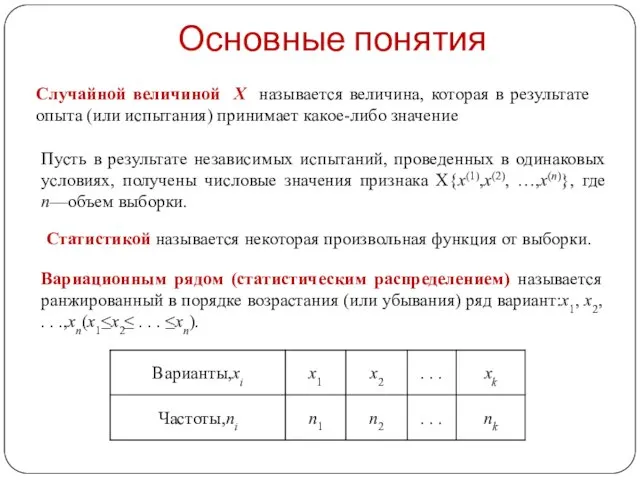
Статистикой называется некоторая произвольная функция от выборки.
Случайной величиной X называется величина, которая в результате опыта (или испытания) принимает какое-либо значение
Пусть в результате независимых испытаний, проведенных в одинаковых условиях, получены числовые значения признака X{x(1),x(2), …,x(n)}, где n—объем выборки.
Вариационным рядом (статистическим распределением) называется ранжированный в порядке возрастания (или убывания) ряд вариант:x1, x2, . . .,xn(x1≤x2≤ . . . ≤xn).
Основные понятия

Интервальный вариационный ряд
1. Вычисляют размах R варьирования признака Х как разность между наибольшим xmax и наименьшим xmin значениями признака:
R =xmax-xmin.
2. Размах R варьирования признака Х делится на k равных частей. Число k выбирают, пользуясь одним из следующих правил:
3. Длина h каждого частичного интервала определяется по формуле: h=R/k.
4. За начало x0 первого интервала рекомендуется[6] брать величину x0=xmin-0,5h.
5. Конец xk последнего интервала находят по формуле xk=xmax+0,5h.

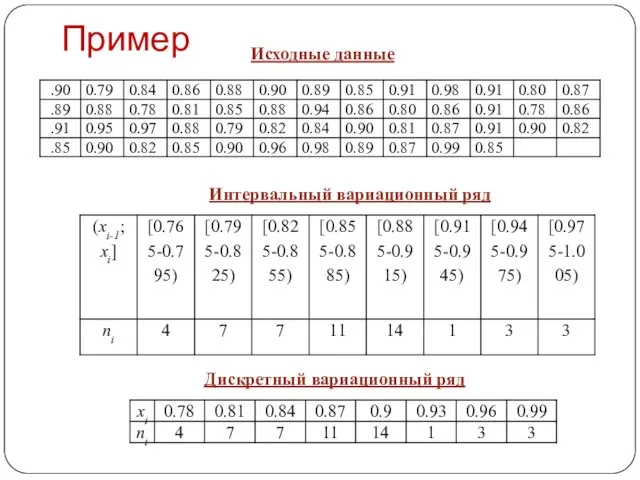
Пример
Исходные данные
Интервальный вариационный ряд
Дискретный вариационный ряд

Построение интервального вариационного ряда
1. Рассчитаем размах варьирования:
где xmin – наименьшая варианта данной выборочной совокупности;
xmax – наибольшая варианта данной выборочной совокупности.
2. Вычислим число равных частей, на которое нужно разделить размах варьирования:
3. Вычислим шаг h (длину интервалов):
4. Вычислим начальное значение первого интервала x0 и конечное значение последнего интервала xk:
,
.

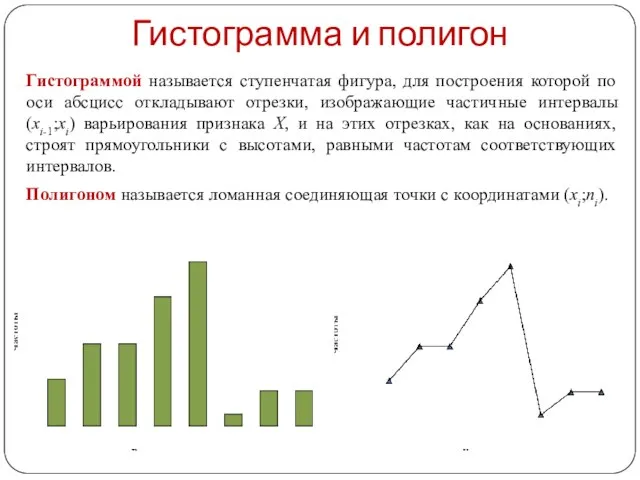
Гистограмма и полигон
Гистограммой называется ступенчатая фигура, для построения которой по оси абсцисс откладывают отрезки, изображающие частичные интервалы (xi-1;xi) варьирования признака Х, и на этих отрезках, как на основаниях, строят прямоугольники с высотами, равными частотам соответствующих интервалов.
Полигоном называется ломанная соединяющая точки с координатами (xi;ni).

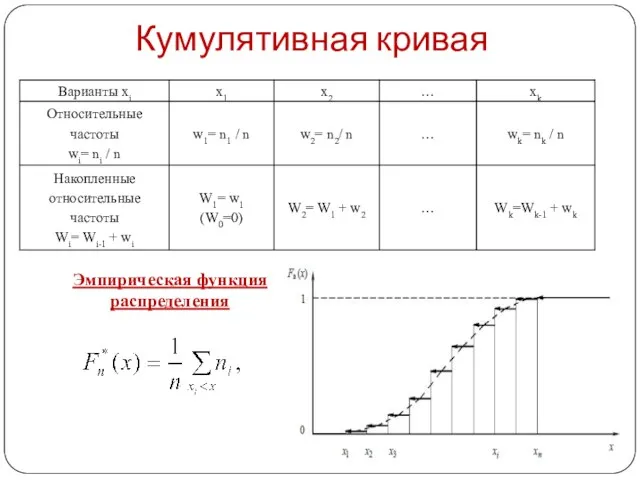
Кумулятивная кривая
Эмпирическая функция распределения
.

Центральная тенденция
Выборочная средняя
Примечание: При анализе данных средним не следует злоупотреблять, необходимо учитывать его свойства и ограничения. Известны характеристики "средняя температура по больнице" или "средняя высота дома", показывающие некорректность использования этой меры центральной тенденции для некоторых случаев.
Свойства среднего
При расчете среднего не допускаются пропущенные значения данных.
Информативность среднего значения переменной высока, если известен ее доверительный интервал.
С увеличением размера выборки точность оценки среднего возрастает.
С увеличением разброса значений выборки надежность среднего падает.

Центральная тенденция
Медианой Me называют варианту которая делит вариационный ряд на две равные по числу вариант части.
При нечетном объеме выборки n=2k+1
При четном объеме выборки n=2k
Примечание: Для определения медианы выборка должна быть обязательно упорядочена.
Me=xk+1

Центральная тенденция
Модой Mo называют варианту, которая имеет наибольшую частоту.
Коэффициент вариации - меры разброса признака относительно его среднего значения.
Примечание: Если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.

Дисперсия
Если объем выборки n>50, то рассчитывают исправленную дисперсию:
Формула расчета дисперсии для несгруппированных данных
Формула расчета дисперсии для сгруппированных данных
Выборочное среднеквадратическое отклонение

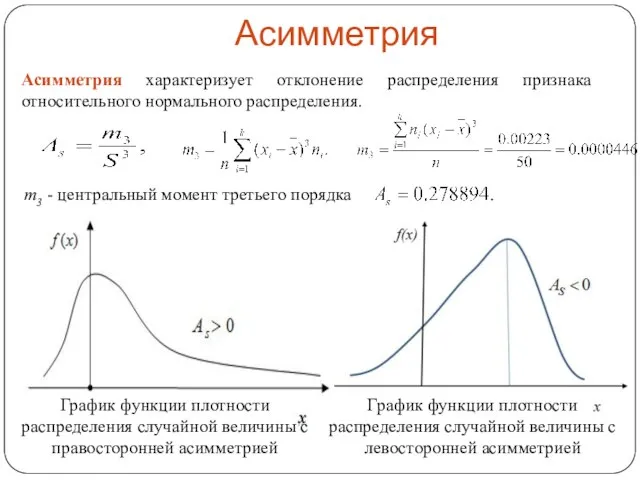
Асимметрия
Асимметрия характеризует отклонение распределения признака относительного нормального распределения.
m3 - центральный момент третьего порядка
График функции плотности распределения случайной величины с правосторонней асимметрией
График функции плотности распределения случайной величины с левосторонней асимметрией

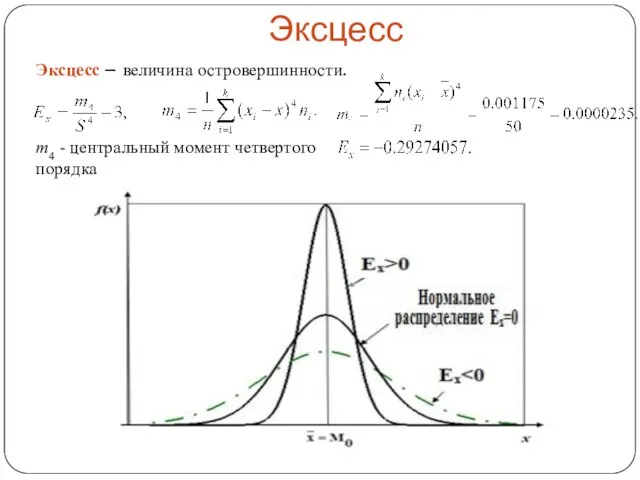
Эксцесс
Эксцесс – величина островершинности.
m4 - центральный момент четвертого порядка

Доверительные интервалы
Для математического ожидания
Для дисперсии
где, -γ-квантиль распределения Стьюдента с n-1 степенью свободы.
Примечание: Для поиска tγ можно воспользоваться функцией Excel =СТЬЮДРАСПОБР(1-γ, n-1).

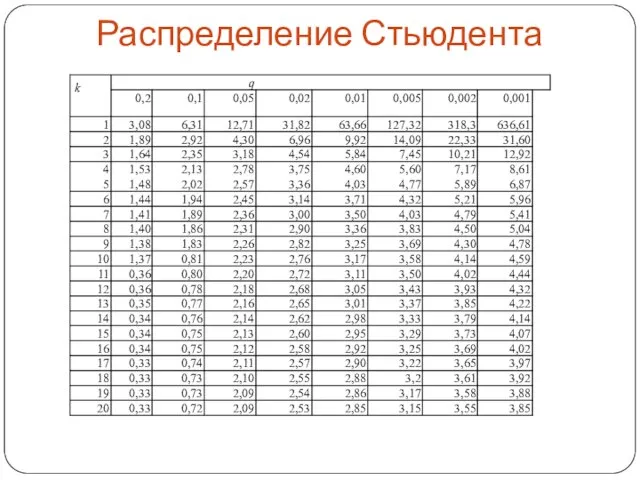
Распределение Стьюдента