Деление отрезка в данном отношении

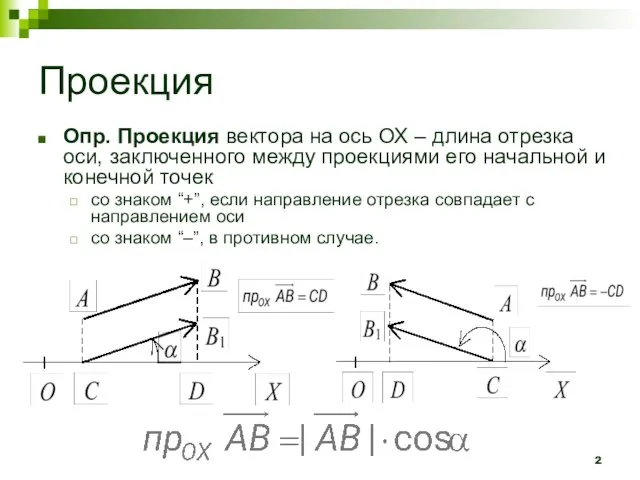
Проекция
Опр. Проекция вектора на ось ОХ – длина отрезка оси, заключенного между проекциями его начальной и конечной точек
со знаком “+”, если направление отрезка совпадает с направлением оси
со знаком “–”, в противном случае.

Свойства проекции
1.
2.

Теорема. Декартовы прямоугольные координаты вектора равны проекциям вектора на соответствующие оси декартовой прямоугольной с/к.
Из опр. проекции ⇒
где α, β, γ – углы наклона вектора к осям OX, OY, OZ.
По т.Пифагора

Направляющие косинусы

Скалярное произведение векторов
Ск. пр. – операция умножения вектора на вектор, в результате которой получается скаляр (число).

Свойства
1.
2.
3. , где λ - константа
4. Если векторы и коллинеарны, то
4а.

Свойства
5.
6.
7.
8.

Скалярное произведение в координатной форме
Пусть
Тогда

Правая тройка.
Если смотреть с конца вектора , то кратчайший поворот от к происходит против часовой стрелки.
Векторное произведение
Опр. Векторным произведением векторов и называется вектор , который
1. и
2.
3. - правая тройка

Свойства
1.
2.
3.
Критерий коллинеарности
Если , то

Векторное произведение в координатной форме
0
0
0

Векторное произведение в координатной форме