Преобразование подобия

Являются ли подобными:
а) два прямоугольника, отличных от квадрата: картина в рамке и картина без рамки, если ширина рамки всюду одинакова (см. рис);
б) литровая и пол-литровая бутылки колы?
Пример 1

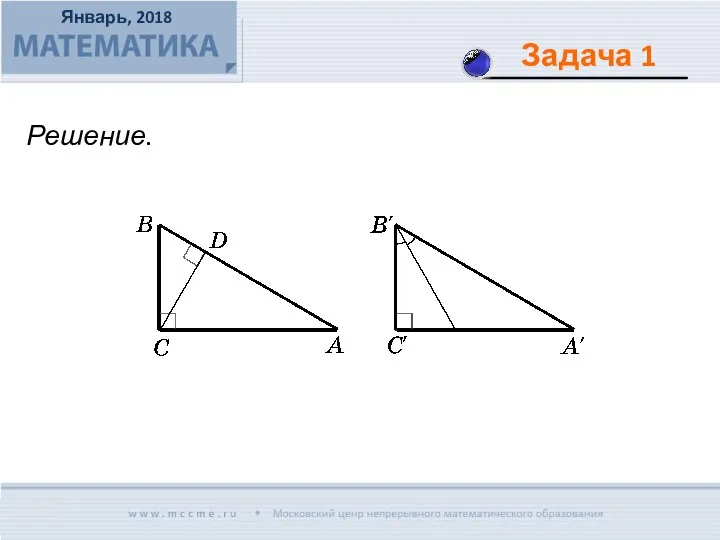
Докажите, что два четырехугольника подобны, если
у них соответственно равны три угла и углы между диагоналями.
Пример 2

Решение.

Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Обязательно ли подобны оставшиеся части?

Решение.

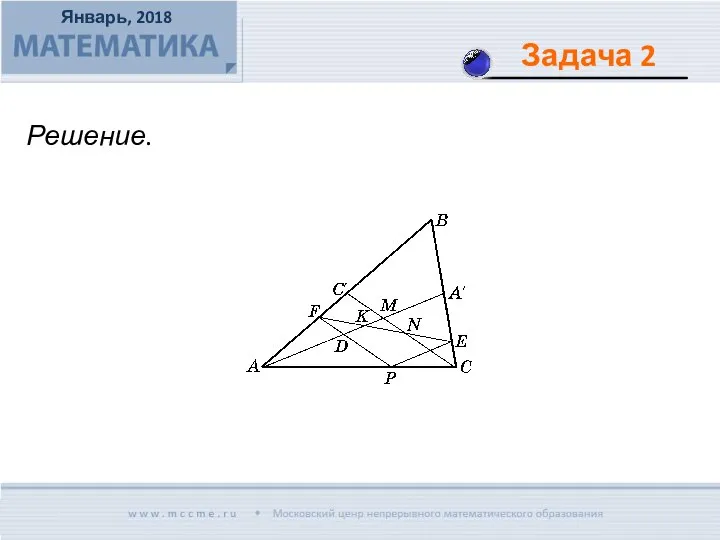
Через произвольную внутреннюю точку Р стороны АС треугольника АВС проведены прямые, параллельные его медианам AA' и СС'. Эти прямые пересекают стороны ВС и АВ в точках Е и F соответственно. Докажите, что отрезок ЕF делится медианами AA’ и СС’ на три равные части.

Решение.

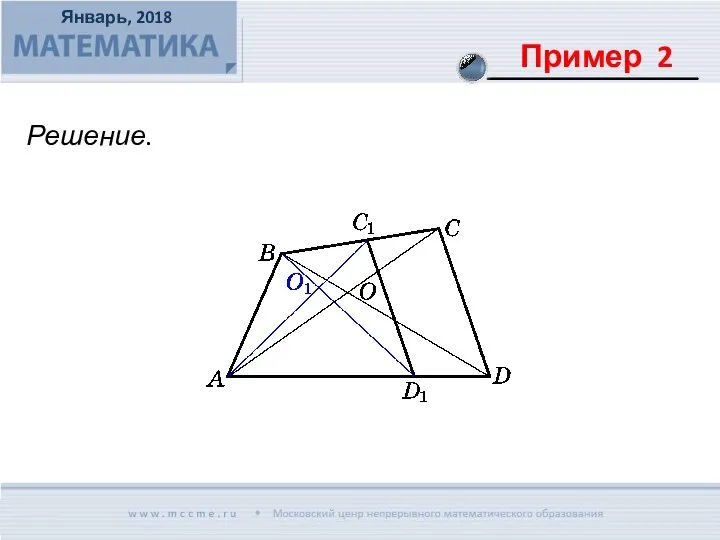
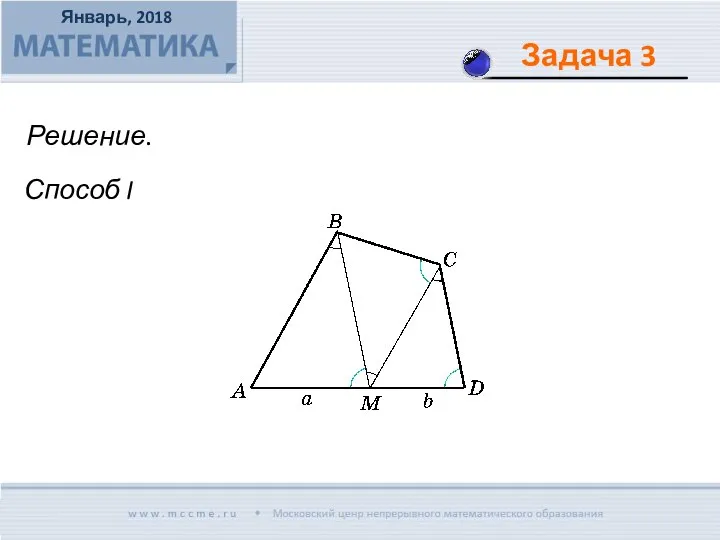
Во вписанном четырехугольнике АВСD точка М лежит на стороне AD, причем BM ǁ CD и CM ǁ BA. Найдите ВС, если АМ = а, DM = b.

Решение.
Способ I

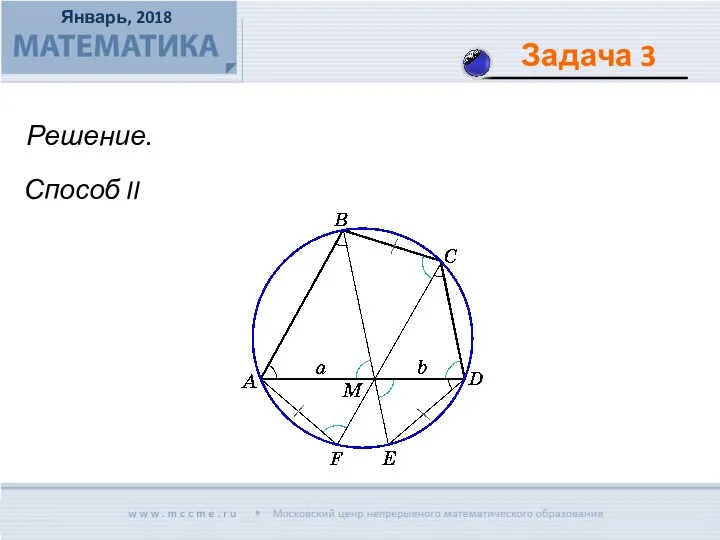
Решение.
Способ II

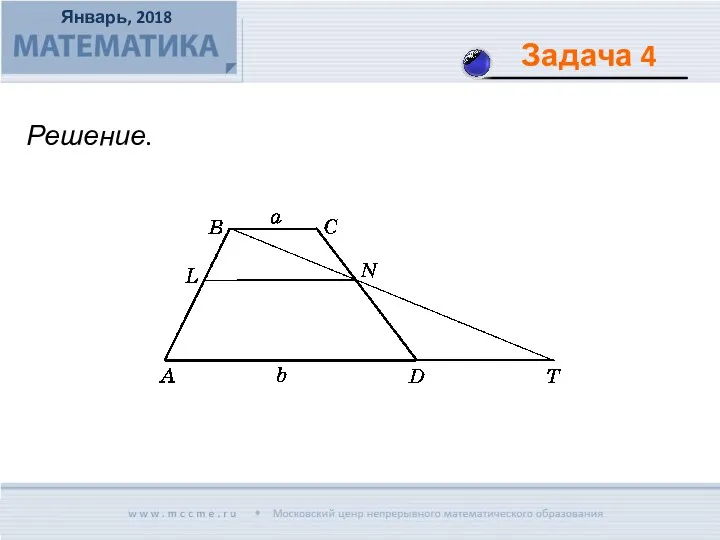
В трапеции АВСD с основаниями ВС = а и AD = b проведен отрезок LN = ab с концами на боковых сторонах. Докажите, что он разделил трапецию на две подобные.

Решение.

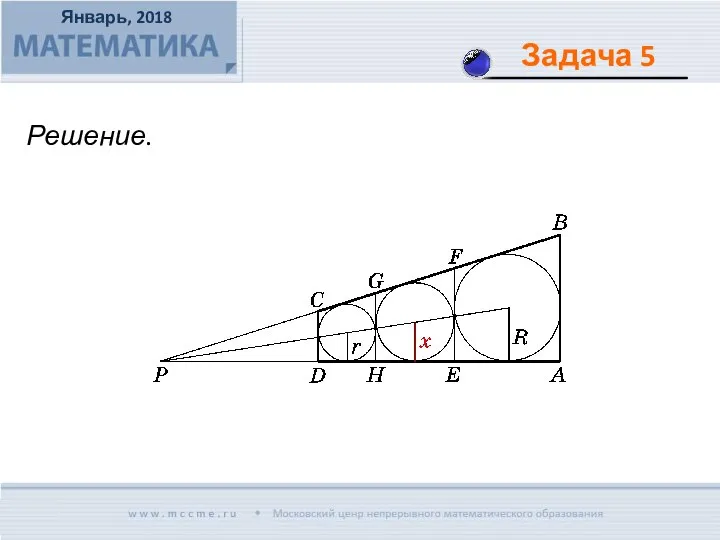
Трапеция разделена на три трапеции прямыми, параллельными основаниям. Известно, что в каждую из трех получившихся трапеций можно вписать окружность. Найдите радиус окружности, вписанной
в среднюю трапецию, если радиусы окружностей, вписанных в две крайние, равны R и r.

Решение.

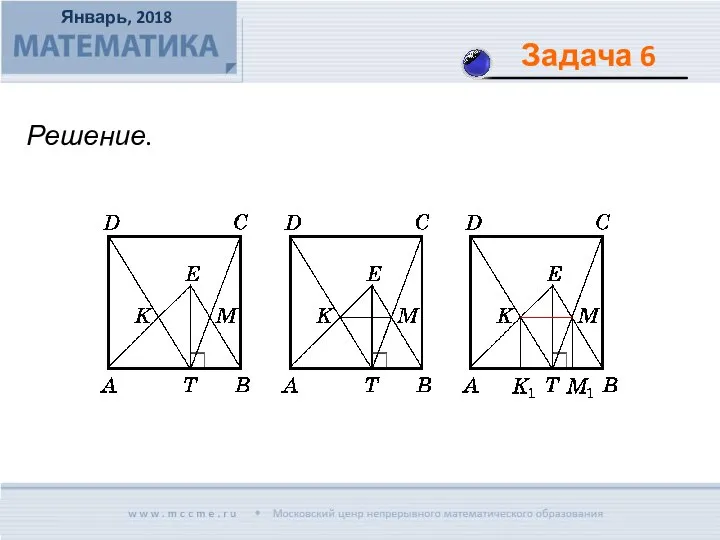
Внутри квадрата ABCD взята точка Е, ET – высота треугольника АВЕ, K – точка пересечения прямых DT и AE, М – точка пересечения прямых СТ и ВЕ. Докажите, что отрезок KМ является стороной квадрата, вписанного в треугольник АВЕ.

Решение.

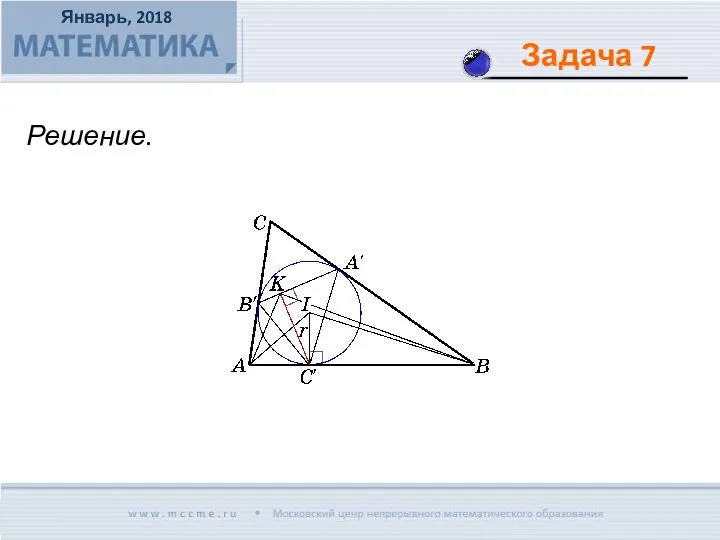
Вписанная окружность треугольника ABC касается его сторон ВС, АС и АВ в точках A', B' и C' соответственно. Точка K – проекция точки C' на прямую A'B'. Докажите, что KC' – биссектриса угла AKB.

Решение.

Докажите, что существует такой невыпуклый шестиугольник, у которого каждый угол равен либо 90°, либо 270°, что его можно разрезать на два подобных ему и неравных между собой шестиугольника.