Слайд 2ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Слайд 3ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Метод введения нового аргумента
Метод разложения
Метод замены переменной (метод подстановки)
Метод интегрирования

по частям
Слайд 8Числа а и b называются соответственно нижним и верхним пределом интегрирования, f(x)

– подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования, отрезок [а; b] –областью (отрезком) интегрирования. Функция у = f(x), для которой на отрезке [а; b] существует определенный интеграл , называется интегрируемой на этом отрезке.
Слайд 10ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА












 Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Тождественные преобразования тригонометрических выражений
Тождественные преобразования тригонометрических выражений Пифагор и музыка
Пифагор и музыка Тест по теме Векторы в пространстве. 11 класс
Тест по теме Векторы в пространстве. 11 класс Викторина О, счастливчик (шуточные тесты математика вокруг нас)
Викторина О, счастливчик (шуточные тесты математика вокруг нас) Вероятность случайного события
Вероятность случайного события Вероятность события 9 класс
Вероятность события 9 класс Устная работа. Вычисления
Устная работа. Вычисления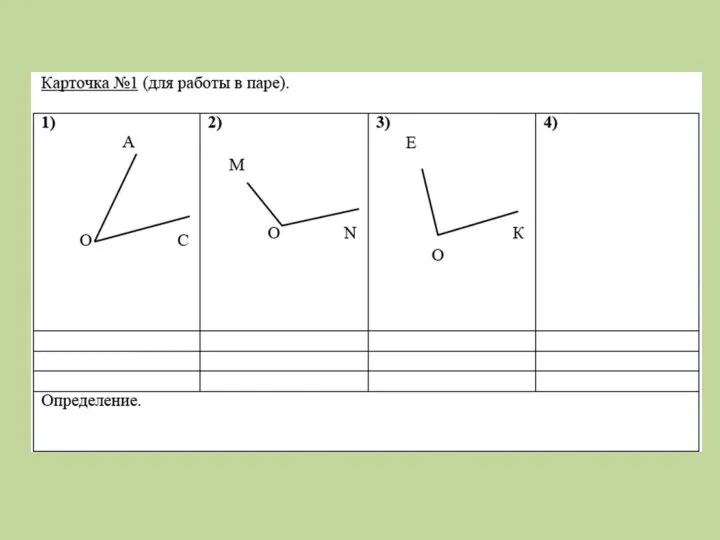 Смежные углы. Карточки для работы в паре
Смежные углы. Карточки для работы в паре В мире случайных закономерностей. Введение в вероятность. 5 класс
В мире случайных закономерностей. Введение в вероятность. 5 класс Нахождение sin и tg
Нахождение sin и tg Разложение многочлена на множители
Разложение многочлена на множители Задания по математике для 3 класса
Задания по математике для 3 класса Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Стереометрия в задачах ЕГЭ
Стереометрия в задачах ЕГЭ Числовые последовательности
Числовые последовательности Движения. 9-й класс
Движения. 9-й класс Умножение дробей
Умножение дробей Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Вычисление определителя третьего порядка по правилу треугольников
Вычисление определителя третьего порядка по правилу треугольников Решение заданий олимпиады по математике
Решение заданий олимпиады по математике Алгоритм задачи
Алгоритм задачи Стационарный режим теплообмена с фазовым переходом
Стационарный режим теплообмена с фазовым переходом Показательные неравенства 11 класс
Показательные неравенства 11 класс Углы треугольника
Углы треугольника Обработка данных. Задачи локального и глобального интерполирования
Обработка данных. Задачи локального и глобального интерполирования Посчитай кубики в постройке
Посчитай кубики в постройке Презентация мера угла, синус, косинус
Презентация мера угла, синус, косинус