Содержание
- 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют любую ее первообразную
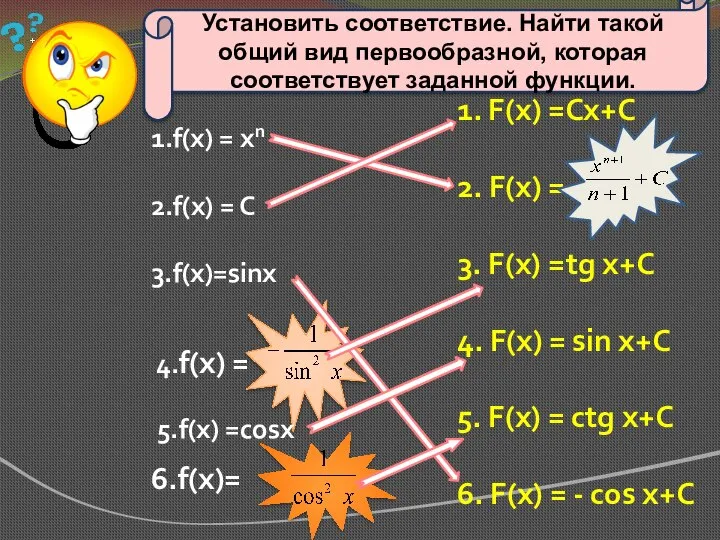
- 3. 1.f(x) = хn 2.f(x) = C 3.f(x)=sinx 4.f(x) = 6.f(x)= 1. F(x) =Сх+С 2. F(x) =
- 4. Свойства интеграла
- 5. Свойства интеграла
- 6. Основные методы интегрирования Табличный. 2.Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. 3.Интегрирование с
- 7. Таблица неопределенных интегралов
- 8. Таблица неопределенных интегралов
- 9. Найти первообразные для функций: F(x) = 5 х² + C F(x) = х³ + C F(x)
- 10. Верно ли что: а) в) б) г)
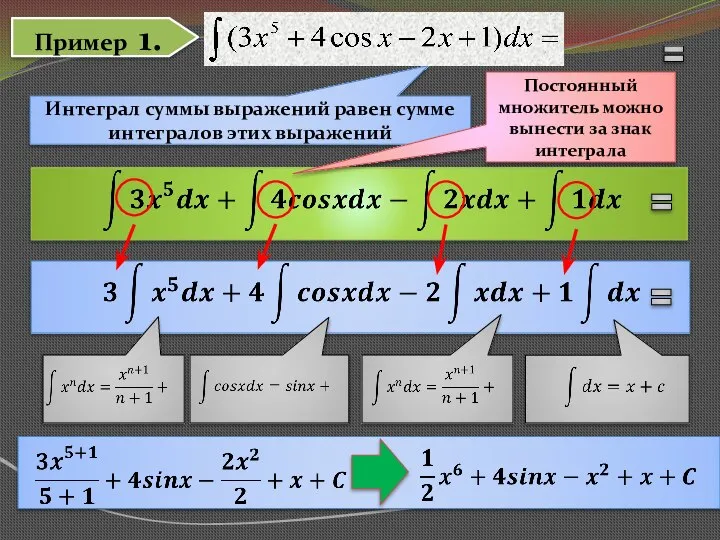
- 11. Пример 1. Интеграл суммы выражений равен сумме интегралов этих выражений Постоянный множитель можно вынести за знак
- 12. Пример 2. Проверить решение Записать решение:
- 13. Пример 3. Проверить решение Записать решение:
- 14. Пример 4. Проверить решение Записать решение: Введем новую переменную и выразим дифференциалы:
- 15. Пример 5. Проверить решение Записать решение:
- 16. Cамостоятельная работа Найти неопределенный интеграл Проверить решение Уровень «А» (на «3») Уровень «В» (на «4») Уровень
- 17. Задание Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.
- 18. При сведении данного интеграла к табличному часто используется следующее преобразование дифференциала (операция «подведения под знак дифференциала»).
- 19. Примеры
- 20. Метод замены переменной (метод подстановки) состоит в преобразовании интеграла в другой интеграл который вычисляется проще, чем
- 21. Пример
- 24. Интегрирование по частям Формула где и – дифференцируемые функции, называется формулой интегрирования по частям. Метод интегрирования
- 25. Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям Интегралы вида где − многочлен, m
- 26. 2. Интегралы вида Здесь полагают за u обозначают остальные сомножители. 3. Интегралы вида где a и
- 27. Пример. Вычислить неопределенные интегралы методом интегрирования по частям.
- 29. Скачать презентацию















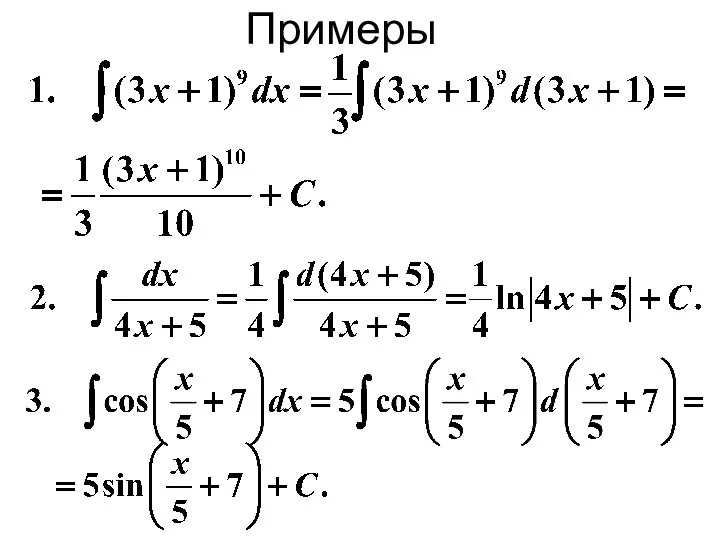


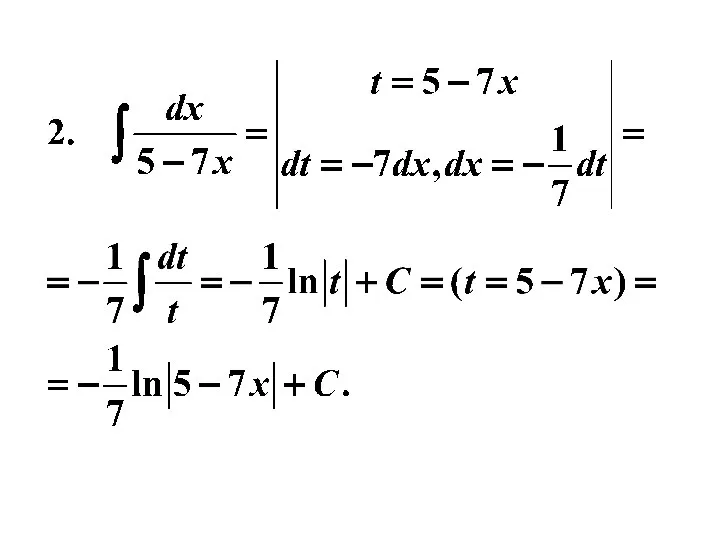
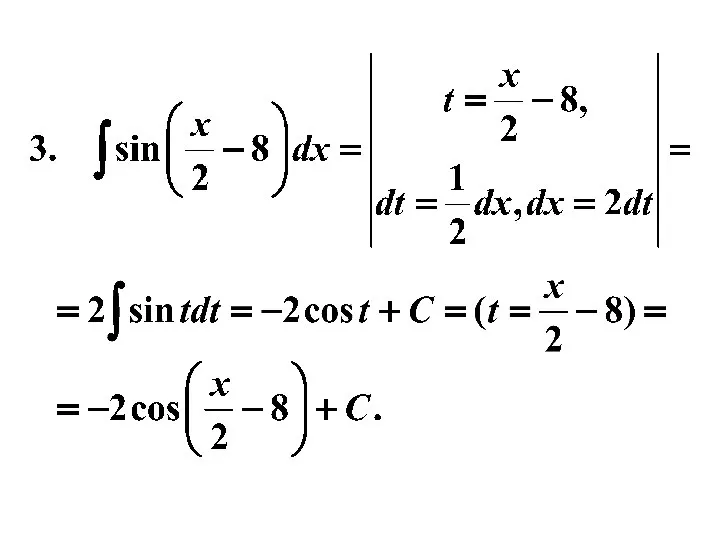




 Сложение положительных и отрицательных чисел
Сложение положительных и отрицательных чисел ГВЭ-9 по математике в 2020-2021 учебном году: структура, содержание КИМ, методика подготовки обучающихся
ГВЭ-9 по математике в 2020-2021 учебном году: структура, содержание КИМ, методика подготовки обучающихся Решение задач на части
Решение задач на части Властивість бісектриси трикутника
Властивість бісектриси трикутника Куб суммы
Куб суммы Прикладные методы расчета и программные комплексы. элементы программирования. Булевы операторы. (7)
Прикладные методы расчета и программные комплексы. элементы программирования. Булевы операторы. (7) Виды графов
Виды графов Величины. Длина
Величины. Длина Показательная функция, ее свойства и график
Показательная функция, ее свойства и график 1_1_matritsy (1)
1_1_matritsy (1) Устный счет в пределах 20
Устный счет в пределах 20 Проект-игра по геометрии Занимательная геометрия
Проект-игра по геометрии Занимательная геометрия Задачи на движение. Движение по реке
Задачи на движение. Движение по реке Презентация на тему Единицы измерения
Презентация на тему Единицы измерения  Postoroenie_gr_trigon_f
Postoroenie_gr_trigon_f Геометрические тела. Построение плоских срезов на геометрических телах
Геометрические тела. Построение плоских срезов на геометрических телах Закрепление знаний. Страничка для любознательных
Закрепление знаний. Страничка для любознательных Я тебя слышу
Я тебя слышу Устный счёт. Вычисли наиболее лёгким способом
Устный счёт. Вычисли наиболее лёгким способом Решение тригонометрических уравнений функционально-графическим методом
Решение тригонометрических уравнений функционально-графическим методом Векторы. Направление вектора
Векторы. Направление вектора Математика. Задача
Математика. Задача Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Линейные неравенства с одной переменной. Обобщающий урок
Линейные неравенства с одной переменной. Обобщающий урок d9d859ec9ada2cfd333ac86c8bdd6908
d9d859ec9ada2cfd333ac86c8bdd6908 Первые уроки в 5 кассе
Первые уроки в 5 кассе Решение логарифмических неравенств
Решение логарифмических неравенств Решение заданий ОГЭ с выбором ответа
Решение заданий ОГЭ с выбором ответа