Nepreryvnost_funktsii (1)

Непрерывность функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точки x0, и в самой точке x0.
Функция y = f(x) называется непрерывной в точке x0 , если существует предел функции в этой точке и он равен значению функции в этой точке:
(1)
Равенство (1) означает выполнение трех условий:
1
Функция y = f(x) определена в точке x0 и в ее окрестности.
2
Функция y = f(x) имеет предел при
3
Предел функции в точке x0 равен значению функции в этой точке.

Непрерывность функции в точке
Так как
то равенство (1) можно записать в виде:
Это значит, что при нахождении предела непрерывной функции можно перейти к пределу под знаком функции:
Равенство справедливо в силу непрерывности функции y = ex

Непрерывность функции в точке
Пусть функция y = f(x) определена в некоторой интервале (a; b).
Возьмем произвольную точку
Разность x – x0 называется приращением аргумента х в точке х0 и обозначается:
х0
y0 = f(x0 )
х
y = f(x )
Разность соответствующих значений функций f(x) – f(x0) называется приращением функции f(x) в точке х0 и обозначается:

Непрерывность функции в точке
х0
y0
Преобразуем равенство (1):
Полученное равенство является еще одним определением непрерывности функции в точке:
Функция y = f(x) называется непрерывной в точке x0 , если она определена в точке x0 и ее окрестности и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

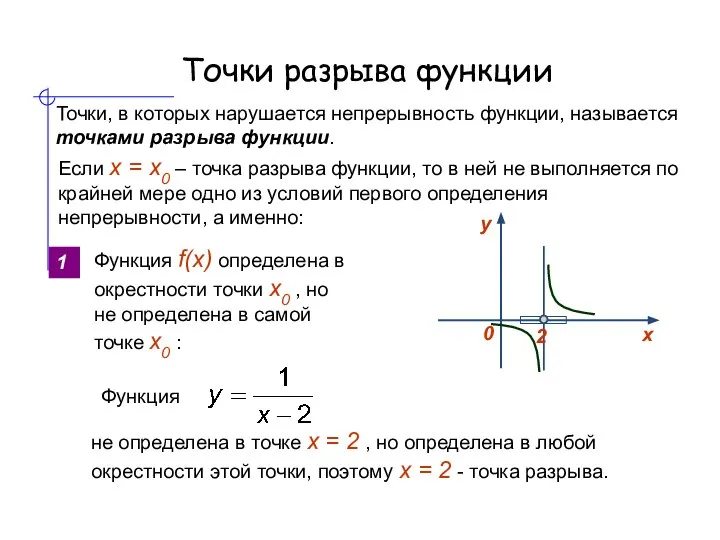
Точки разрыва функции
Точки, в которых нарушается непрерывность функции, называется точками разрыва функции.
Если x = x0 – точка разрыва функции, то в ней не выполняется по крайней мере одно из условий первого определения непрерывности, а именно:
2
Функция f(x) определена в окрестности точки х0 , но не определена в самой точке х0 :
1
не определена в точке х = 2 , но определена в любой окрестности этой точки, поэтому х = 2 - точка разрыва.
Функция

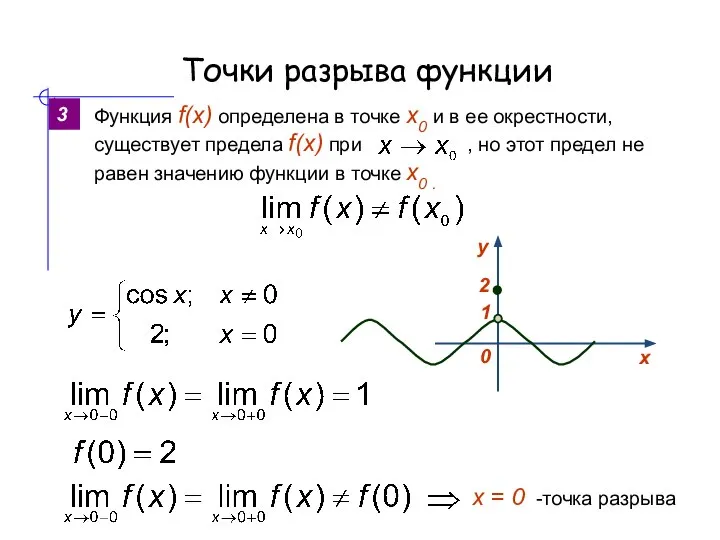
Точки разрыва функции
2
Функция f(x) определена в точке х0 и в ее окрестности, но не существует предела f(x) при
2
определена в точке х = 2 , но но не имеет предела при
Функция
не существует, значит
х = 2 - точка разрыва

Точки разрыва функции
2
3
х = 0 -точка разрыва
1

Точки разрыва функции
Точка разрыва х0 называется точкой разрыва 1 рода функции f(x) , если в этой точке существуют конечные пределы слева и справа:
При этом:
Величину называют скачком функции в точке разрыва 1 рода.

Точки разрыва функции
Точка разрыва х0 называется точкой разрыва 2 рода функции f(x) , если по крайней мере один из односторонних пределов не существует или равен бесконечности.
В примере 1:
х = 2 – точка разрыва 2 рода.

Основные теоремы о непрерывных функциях
Сумма, произведение и частное непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, где знаменатель равен нулю)
Теорема 1
Теорема 2
Пусть функция u = g(x) непрерывна в точке x0, а функция y = f(u) непрерывна в точке u0 = g(x0). Тогда сложная функция y = f(g(x)) непрерывна в точке x0.
Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, при которых эти функции определены.
Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Непрерывность функции в интервале и на отрезке.
Функция y = f(х) называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала.
Функция y = f(х) называется непрерывной на отрезке [a; b], если она непрерывна на интервале (a; b), и в точке x = a непрерывна справа:
а в точке x = b непрерывна слева: