Вариационные ряды

Опорный конспект
Решите задачи на повторение (5, 6 слайд).
2. Запишите алгоритм обработки статистических данных.
3. Перечислите основные понятия математической статистики и их определения.
4. Какой основной метод обработки статистических данных?
5. Выполнить решение задач на 19 слайде.

Математическая статистика – раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений.
Задачи математической статистики:
Сбор, хранение и обработка информации.
Установление и исследования различного рода зависимостей на основании экспериментальных данных.
Изучение вероятностных характеристик моделей реальных явлений.
Разработка прогнозов, оценка их достоверности.

Повторение:
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Модой ряда чисел называется число, которое встречается в данном ряду чаще других. (Mo)
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда. (Me)

Возраст учеников, которые занимаются в кружке по математике, дан ниже:
Найдите:
а) размах; б) моду; в) медиану;
г) среднее значение.

В ряду чисел
3, 8, 15, 30, ___, 24
пропущено одно число. Найди его если:
а) среднее арифметическое ряда равно 18;
б) размах ряда равен 40;
в) мода ряда равна 24.

Статистические данные – сведения о числе объектов, какой- либо обширной совокупности, обладающих теми или иными признаками (число студентов, родившихся в 1980 г; балловые результаты ЕГЭ в городе).
Основной метод обработки статистических данных – выборочный метод.
Алгоритм обработки статистических данных:
Упорядочение и группировка данных;
Составление таблиц распределения данных;
Построение графиков распределения данных;
Расчет основных числовых характеристик статистических данных.

Выборку, представляющую собой неубывающую последовательность чисел, называют вариационным рядом.
Генеральная совокупность – совокупность всех исследуемых объектов.
Основные понятия математической статистики:
Выборка – совокупность случайно отобранных объектов генеральной совокупности.
Объем выборки – число объектов выборки или генеральной совокупности.
Размах выборки – разность между наибольшим и наименьшим значением числовой выборки.

Основные понятия математической статистики:
Вариантой называют каждое полученное значение данных конкретного измерения:
Кратностью или частотой варианты называют число, показывающее, сколько раз варианта встретилась в данном измерении:
Относительной частотой значений выборки называют отношение частоты варианты к объему выборки:
Статистическим рядом называют последовательность пар:

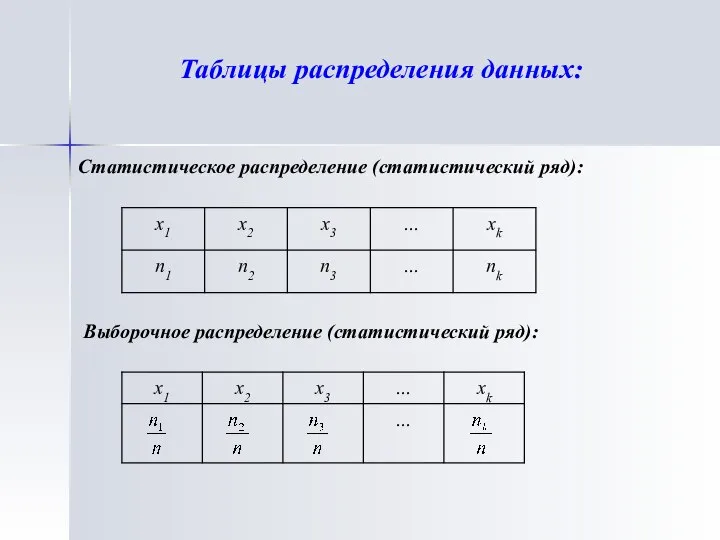
Таблицы распределения данных:
Статистическое распределение (статистический ряд):
Выборочное распределение (статистический ряд):

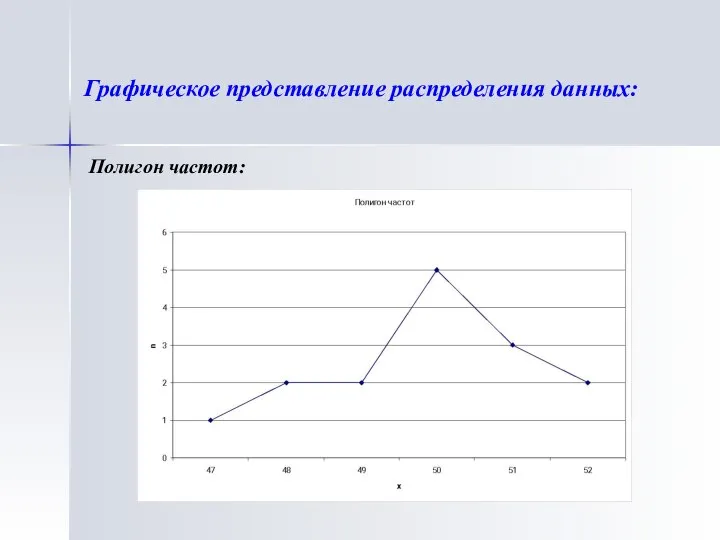
Графическое представление распределения данных:
Полигон частот:

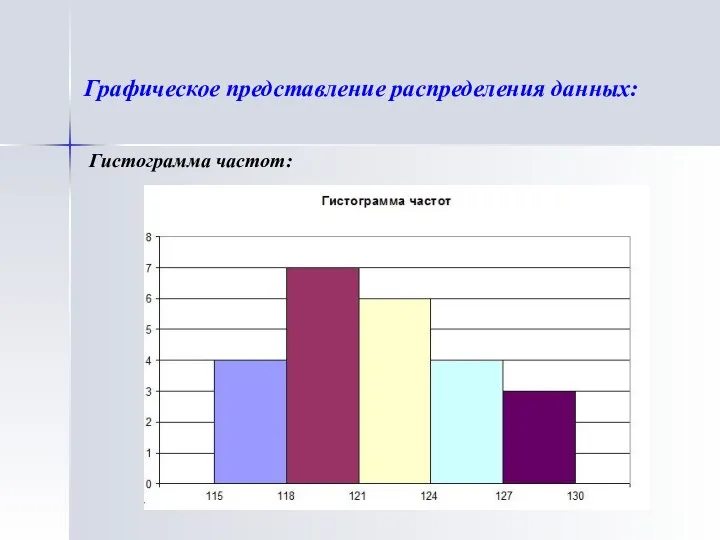
Графическое представление распределения данных:
Гистограмма частот:

Выборочные характеристики:
Выборочным математическим ожиданием (выборочным средним) называют среднее арифметическое значение выборки:
Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений выборки от выборочного среднего:
или
или
Среднее квадратичное отклонение:

Практическое применение средних величин
(выборочных характеристик)в медицине:
Для оценки состояния здоровья, например параметров физического развития (средний рост, средний вес, средний объем емкости легких), соматических показателей (средний уровень сахара в крови, средний пульс).
Для оценки организации работы лечебно-профилактических и санитарно-противиэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников.
Для оценки состояния окружающей среды.

Задача:
В результате измерения роста 7 - летних детей (см) получена выборка: 118, 121, 115, 125,125,117,124,120,120,119,121,119, 122, 127, 118, 120,123,130,123,116, 124, 127, 120, 122.
Представьте эти данные в виде дискретного статистического ряда распределения и постройте полигон частот. Постойте гистограмму, если число частичных промежутков равно 5. Определите среднее значение роста детей и отклонение от него.
Решение:
Составим вариационный ряд выборки: 115, 116, 117, 118, 118, 119, 119, 120, 120, 120, 120, 121, 121, 122, 122, 123, 123, 124,124, 125, 125, 127, 127, 130.
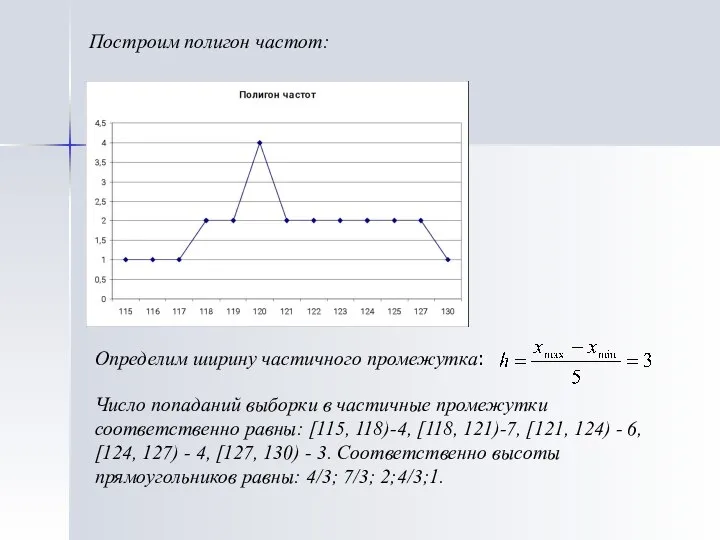
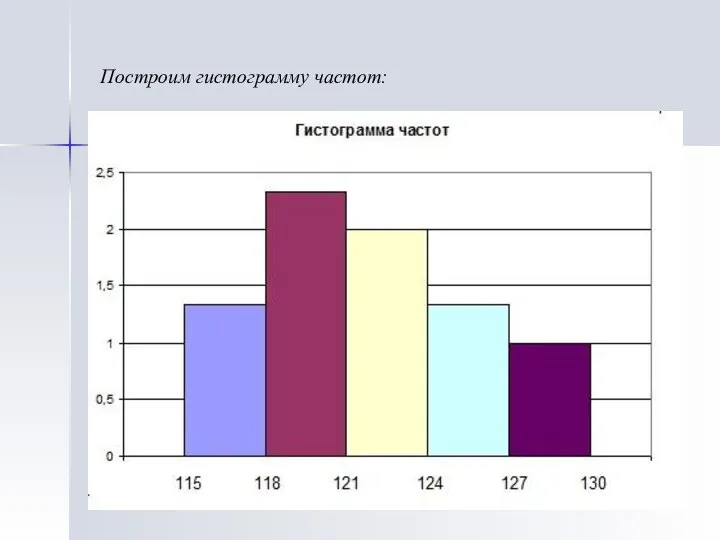
Запишем статистическое распределение (статистический ряд):

Построим полигон частот:
Определим ширину частичного промежутка:
Число попаданий выборки в частичные промежутки соответственно равны: [115, 118)-4, [118, 121)-7, [121, 124) - 6, [124, 127) - 4, [127, 130) - 3. Соответственно высоты прямоугольников равны: 4/3; 7/3; 2;4/3;1.

Построим гистограмму частот:

Вычислим среднее значение выборки (средний рост детей):
см
Вычислим дисперсию:
Вычислим среднее квадратичное отклонение:
см