- Главная
- Математика
- Узоры таблицы пифагора

Содержание
- 2. Паспорт проекта: В работе изучается свойства таблицы Пифагора «Узоры таблицы Пифгора». Для моделирования и изучения свойств
- 3. Задача работы: 1. На основе анализа научной, исторической и методической литературы получить теоретические знания о таблице
- 4. Глава 1. Теоретическая часть исследования 1.1. История таблицы Пифагора Таблица умножения или как её ещё называют
- 5. Вообще современная таблица умножения появилась на Руси благодаря математику Леонтию Филипповичу Магницкому. Он в 1707 году
- 6. 1.2. Свойства и закономерности таблицы Пифагора Все мы пытались заучить таблицу умножения и не пытались понять
- 7. Давайте разберемся, чем же таблица Пифагора лучше, чем обычная таблица умножения? Я попытаюсь ответить на этот
- 8. 1.3 Язык программирования Pascal ABC Для исследования «узоров таблицы Пифагора» я решил использовать язык программирования Pascal
- 9. Глава 2. Практическая часть исследования 2.1. Моделирование зависимости между числами – множителями таблицы Пифагора средствами Pascal
- 10. Program Pifagor; uses graphABC; var i, j, ost: byte; zvet1, zvet2 : color; begin for i:=1
- 11. 2.2. Исследование закономерности таблицы Пифагора с помощью программы В результате своего исследования я выяснил, что, чем
- 12. Рисунок 2.2
- 14. Скачать презентацию
Слайд 2Паспорт проекта:
В работе изучается свойства таблицы Пифагора «Узоры таблицы Пифгора». Для моделирования
Паспорт проекта:
В работе изучается свойства таблицы Пифагора «Узоры таблицы Пифгора». Для моделирования

Цель работы:
Составить программу для исследования одного из свойств таблицы Пифагора
Объект исследования:
Объектом исследования выступает таблица Пифагора
Придмет исследования:
Предметом исследования является закономерность таблицы Пифагора
Гипотеза исследования:
Изучения и исследование закономерности таблицы Пифагора позволит понять, что лежит в основе «удивительных узоров Пифагора»
Результат:
Результат моей работы-это полученные знания по построению красивых узоров в удивительной «таблице Пифагора» с помощью программирования.
Слайд 3Задача работы:
1. На основе анализа научной, исторической и методической литературы получить теоретические
Задача работы:
1. На основе анализа научной, исторической и методической литературы получить теоретические

2. Выделить необходимые знания о закономерности в таблице Пифагора, отвечающей за «узоры».
3. Изучить среду программирования Pascal ABC.
4. Построить алгоритм, позволяющий исследовать указанную закономерность.
5. Составить программу на языке Pascal ABC для исследования закономерности.
6. Исследовать с помощью программы таблицу Пифагора и сделать выводы.
Слайд 4 Глава 1. Теоретическая часть исследования
1.1. История таблицы Пифагора
Таблица умножения или
Глава 1. Теоретическая часть исследования
1.1. История таблицы Пифагора
Таблица умножения или

В 493 году появился вариант, его предложил учёный, которого звали Викторий Аквитанский, он записал таблицу, которая состояла из 98 столбцов, таблица была записана римскими цифрами в результате умножения чисел от 2 до 50. А ещё шотландский физик и профессор математики Джон Лесли в 1820-м году в своей книге «Философия арифметики» опубликовал таблицу умножения, в которой находилось до 99 столбцов. Он стал первым человеком, который рекомендовал своим ученикам учить эту таблицу
Слайд 5Вообще современная таблица умножения появилась на Руси благодаря математику Леонтию Филипповичу Магницкому.
Вообще современная таблица умножения появилась на Руси благодаря математику Леонтию Филипповичу Магницкому.

Слайд 61.2. Свойства и закономерности таблицы Пифагора
Все мы пытались заучить таблицу умножения и
1.2. Свойства и закономерности таблицы Пифагора
Все мы пытались заучить таблицу умножения и

Эта таблица скрывает в себе много секретов. Конечно, можно их не разбирать, а просто выучить эта таблицу. Это будет легко, но совсем неинтересно. А вот, если мы будем разбирать каждое её свойство, то работа с таблицей может очень сильно увлечь любого человека. Когда мы изучим загадки таблицы Пифагора, мы будем ее знать и пользоваться ее скрытыми формулами.
Слайд 7Давайте разберемся, чем же таблица Пифагора лучше, чем обычная таблица умножения? Я
Давайте разберемся, чем же таблица Пифагора лучше, чем обычная таблица умножения? Я

Мы все знаем математическое правило, что от перестановки мест множителей произведение не меняется. Это правило действует и в таблице Пифагора. Если мы возьмем, например, числа 5 и 6. То разницы не будет, если мы возьмём 5 сверху, а 6 слева и перемножим их. И также, но возьмём 5 справа, а 6 сверху. То разницы не будет.
Давайте посмотрим на еще одно свойство. Если взять любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике — ваше число. И тут умножение получает более глубокий смысл, чем просто сокращенная запись нескольких одинаковых множителей. Это правило из геометрии: площадь прямоугольника равна произведению его сторон.
Слайд 81.3 Язык программирования Pascal ABC
Для исследования «узоров таблицы Пифагора» я решил использовать
1.3 Язык программирования Pascal ABC
Для исследования «узоров таблицы Пифагора» я решил использовать

Используя графические примитивы Pascal ABC можно создавать изображения. Для создания изображений необходимо использовать модуль GraphABC. Это простая графическая библиотека, предназначенная для создания несобытийных графических и анимационных программ. Я использовал графические примитивы, представляющие собой процедуры, осуществляющие рисование в графическом окне.
Я использовал оператор цикла for, оператор выбора case, бинарные операции div и mod, графические примитивы, подпрограммы для работы с пером и кистью. Подробнее о написании программы для исследования свойства «узоры таблицы Пифагора» написано в главе 2.
Слайд 9Глава 2. Практическая часть исследования
2.1. Моделирование зависимости между числами – множителями таблицы Пифагора
Глава 2. Практическая часть исследования
2.1. Моделирование зависимости между числами – множителями таблицы Пифагора
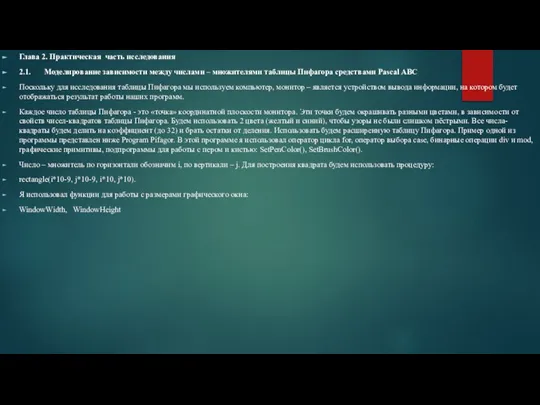
Поскольку для исследования таблицы Пифагора мы используем компьютер, монитор – является устройством вывода информации, на котором будет отображаться результат работы наших программ.
Каждое число таблицы Пифагора - это «точка» координатной плоскости монитора. Эти точки будем окрашивать разными цветами, в зависимости от свойств чисел-квадратов таблицы Пифагора. Будем использовать 2 цвета (желтый и синий), чтобы узоры не были слишком пёстрыми. Все числа-квадраты будем делить на коэффициент (до 32) и брать остатки от деления. Использовать будем расширенную таблицу Пифагора. Пример одной из программы представлен ниже Program Pifagor. В этой программе я использовал оператор цикла for, оператор выбора case, бинарные операции div и mod, графические примитивы, подпрограммы для работы с пером и кистью: SetPenColor(), SetBrushColor().
Число – множитель по горизонтали обозначим i, по вертикали – j. Для построения квадрата будем использовать процедуру:
rectangle(i*10-9, j*10-9, i*10, j*10).
Я использовал функции для работы с размерами графического окна:
WindowWidth, WindowHeight
Слайд 10Program Pifagor;
uses graphABC;
var
i, j, ost: byte;
zvet1, zvet2 : color;
begin
Program Pifagor;
uses graphABC;
var
i, j, ost: byte;
zvet1, zvet2 : color;
begin
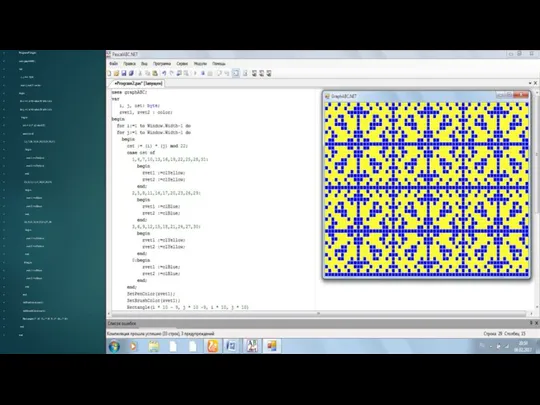
for j:=1 to Window.Width-1 do
begin
ost := (i) * (j) mod 22;
case ost of
1,4,7,10,13,16,19,22,25,28,31:
begin
zvet1 :=clYellow;
zvet2 :=clYellow;
end;
2,5,8,11,14,17,20,23,26,29:
begin
zvet1 :=clBlue;
zvet2 :=clBlue;
end;
3,6,9,12,15,18,21,24,27,30:
begin
zvet1 :=clYellow;
zvet2 :=clYellow;
end;
0:begin
zvet1 :=clBlue;
zvet2 :=clBlue;
end;
end;
SetPenColor(zvet1);
SetBrushColor(zvet1);
Rectangle(i * 10 - 9, j * 10 -9, i * 10, j * 10)
end;
end.
Слайд 112.2. Исследование закономерности таблицы Пифагора с помощью программы
В результате своего исследования я выяснил,
2.2. Исследование закономерности таблицы Пифагора с помощью программы
В результате своего исследования я выяснил,

Я использовал следующие коэффициенты:
ost := (i) * (j) mod 22
ost := (i) * (j) mod 22 mod 5
ost := (2*i) * (2*j) mod 25
ost := (i) * (j) mod 31
ost := (i) * (j) div 5 mod 5
и другие
В приложении 1 я представил коды программ и результаты их выполнения, демонстрирующие загадки таблицы Пифагора. Получилось достаточно красиво.
Задача на изучение свойств таблицы Пифагора средствами Pascal ABC оказалась очень интересной. Оказывается на основе этой древней числовой схемы можно составлять различные мозаики.
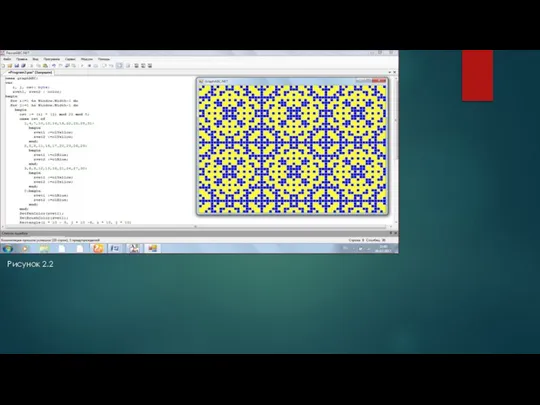
Слайд 12Рисунок 2.2
Рисунок 2.2
 Sam Signal Processing New2
Sam Signal Processing New2 Презентация на тему Преобразование выражений содержащих квадратные корни
Презентация на тему Преобразование выражений содержащих квадратные корни  Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Перпендикулярные прямые
Перпендикулярные прямые Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени Задание из учебника Н.Б. Исиоминой. 3 класс. 2 часть
Задание из учебника Н.Б. Исиоминой. 3 класс. 2 часть Интегральное исчисление
Интегральное исчисление Распределение Максвелла
Распределение Максвелла Презентация на тему Геометрия вокруг нас
Презентация на тему Геометрия вокруг нас  Сравнение числовых выражений (Урок 30)
Сравнение числовых выражений (Урок 30) Решение задач
Решение задач Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania
Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania Длина окружности,
Длина окружности, Прямые на плоскости. Задачи 6 и 7
Прямые на плоскости. Задачи 6 и 7 Решение неравенств второй степени с помощью эскиза параболы
Решение неравенств второй степени с помощью эскиза параболы Правила вычисления производной
Правила вычисления производной Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами  Скрещивающиеся прямые
Скрещивающиеся прямые Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Определение функций. Построение и чтение графиков функций
Определение функций. Построение и чтение графиков функций Построение сечений
Построение сечений Исследовательская работа. Теорема Пифагора
Исследовательская работа. Теорема Пифагора Формула Бернулли
Формула Бернулли Таблицы истинности
Таблицы истинности Взаимное расположение прямой и окружности на плоскости
Взаимное расположение прямой и окружности на плоскости Окружность. 7 класс
Окружность. 7 класс