Содержание
- 2. Алгоритм получения СДНФ
- 3. Алгоритм получения СКНФ привести формулу с помощью равносильных преобразований к КНФ. удалить члены конъюнкции, содержащие переменную
- 4. Алгоритм получения СКНФ
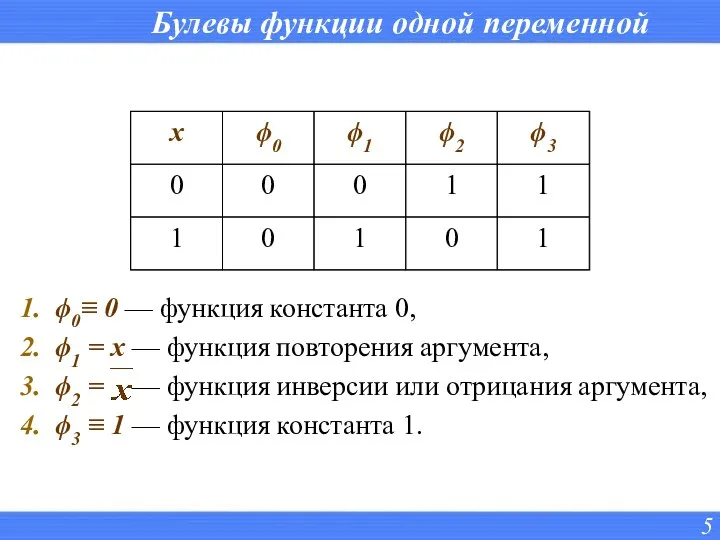
- 5. Булевы функции одной переменной ϕ0≡ 0 — функция константа 0, ϕ1 = x — функция повторения
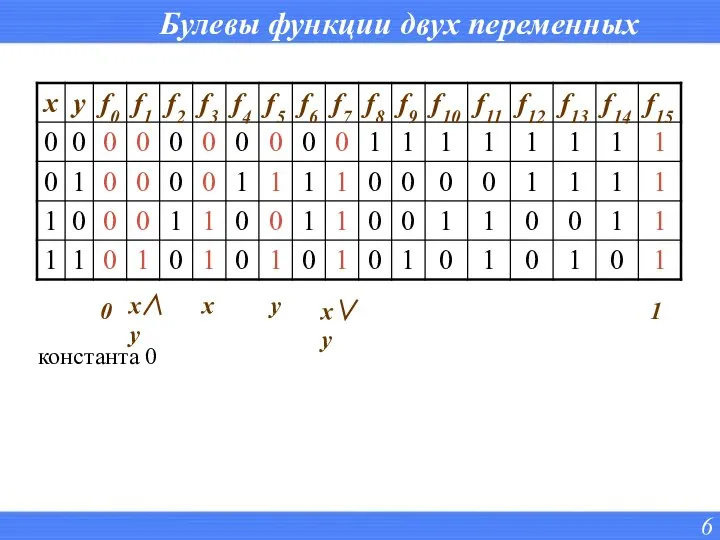
- 6. Булевы функции двух переменных 0 константа 0 x∧y x y x∨y 1
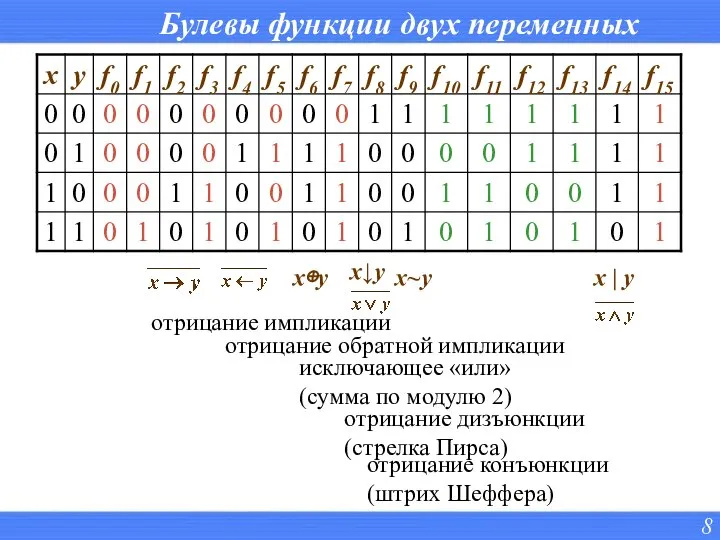
- 7. Булевы функции двух переменных x→y y→x
- 8. Булевы функции двух переменных отрицание импликации отрицание обратной импликации x⊕y исключающее «или» (сумма по модулю 2)
- 10. Двойственные булевы функции Функция f*(x1,…,xn) называется двойственной к функции f(x1,…,xn), если Пример Найти двойственные функции
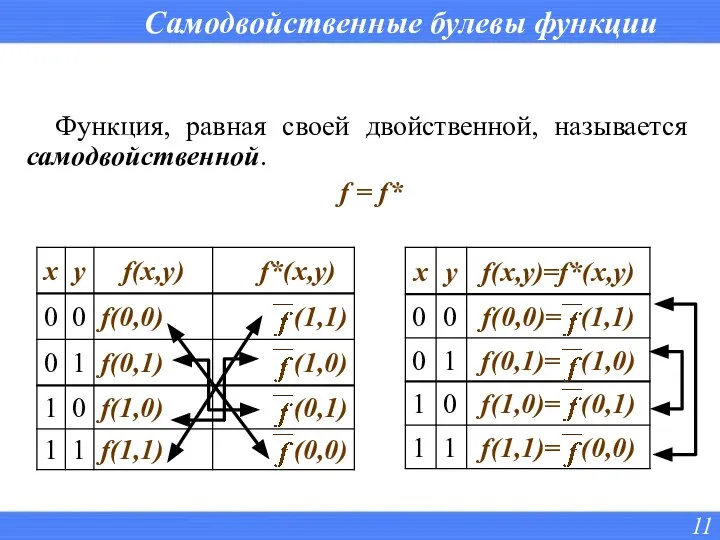
- 11. Самодвойственные булевы функции Функция, равная своей двойственной, называется самодвойственной. f = f*
- 12. Является ли функция f(x,y,z) самодвойственной? Пример f(x,y,z) — несамодвойственная
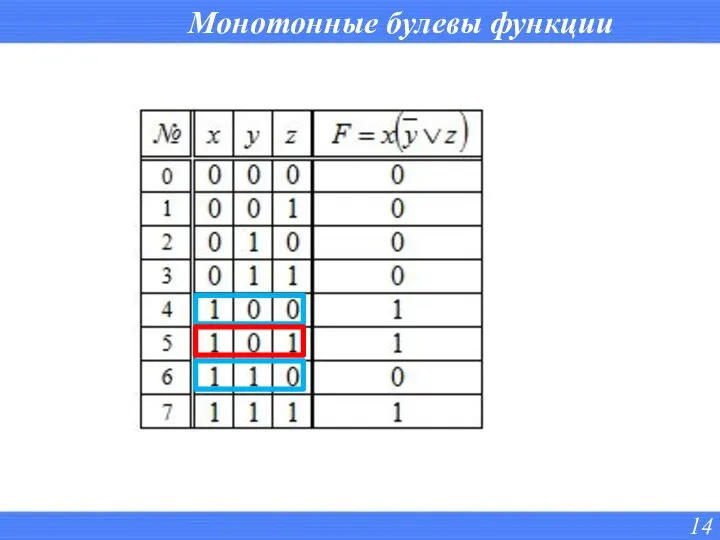
- 13. Монотонные булевы функции
- 14. Монотонные булевы функции
- 15. Линейные булевы функции Многочленами Жегалкина назваются формулы над множеством функций FJ={ 0, 1, ^, +}
- 16. Линейные булевы функции Всякую булеву функцию можно представить единственным полиномом Жегалкина.
- 17. Алгоритм построения полинома Жегалкина по СДНФ Начало. Задана совершенная ДНФ функции f(x1, …, xn). Шаг 1.
- 19. Линейные булевы функции
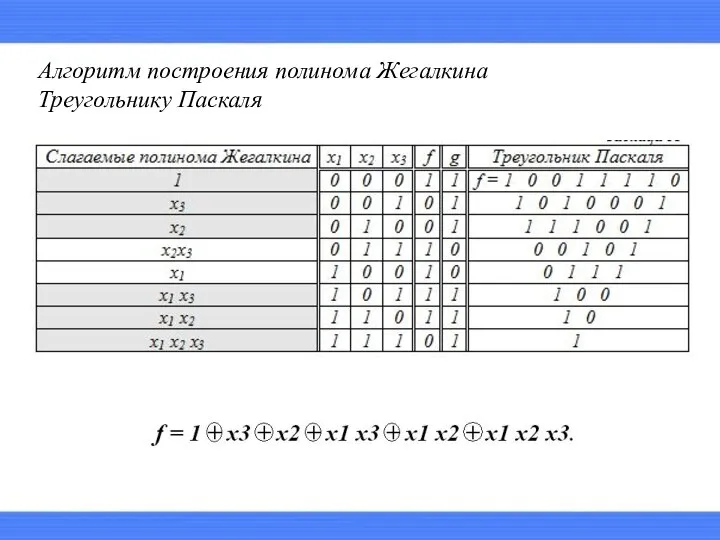
- 20. Алгоритм построения полинома Жегалкина Треугольнику Паскаля
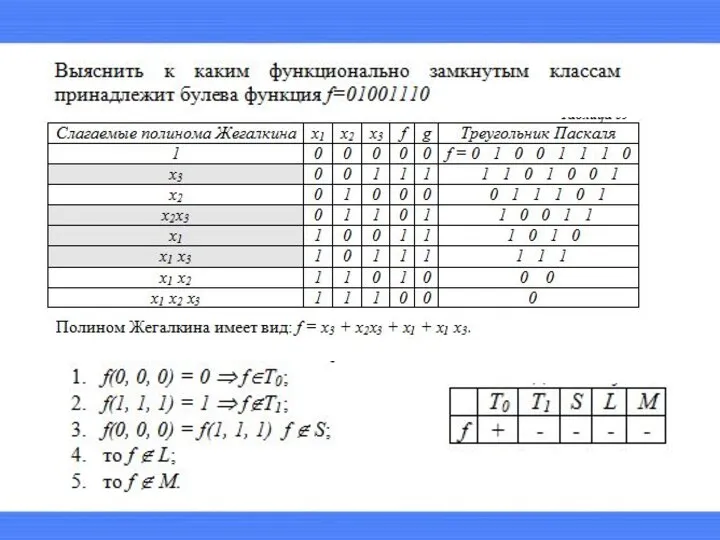
- 21. T0, T1, L, M, S
- 23. Теорема Поста о функциональной полноте Одна из сфер применения булевых функций -- синтез логических схем; при
- 25. Скачать презентацию















 Индивидуальный проект на тему Золотое сечение в природе
Индивидуальный проект на тему Золотое сечение в природе Решите примеры
Решите примеры Первообразная и интеграл
Первообразная и интеграл Математический факультатив
Математический факультатив Промежуточная мерка
Промежуточная мерка Красота многогранников и не только. Из природы в науку
Красота многогранников и не только. Из природы в науку Расстояние между точками
Расстояние между точками Матрицы и определители
Матрицы и определители Первообразная. 11 класс
Первообразная. 11 класс Метод координат. Нахождение углов
Метод координат. Нахождение углов Уравнение с параметром
Уравнение с параметром Построение графиков функций с помощью геометрических преобразований
Построение графиков функций с помощью геометрических преобразований Аксиомы стереометрии и следствия из них
Аксиомы стереометрии и следствия из них Теорема Пифагора
Теорема Пифагора Определение и признаки параллелограмма
Определение и признаки параллелограмма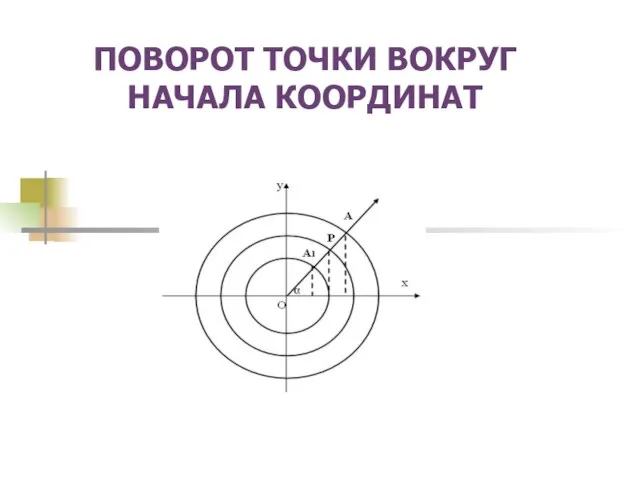 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Несобственные интегралы первого рода
Несобственные интегралы первого рода Многогранники
Многогранники Свойство биссектрисы угла. Свойства серединного перпендикуляра к отрезку
Свойство биссектрисы угла. Свойства серединного перпендикуляра к отрезку Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Модели статистического прогнозирования. Урок 31
Модели статистического прогнозирования. Урок 31 Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей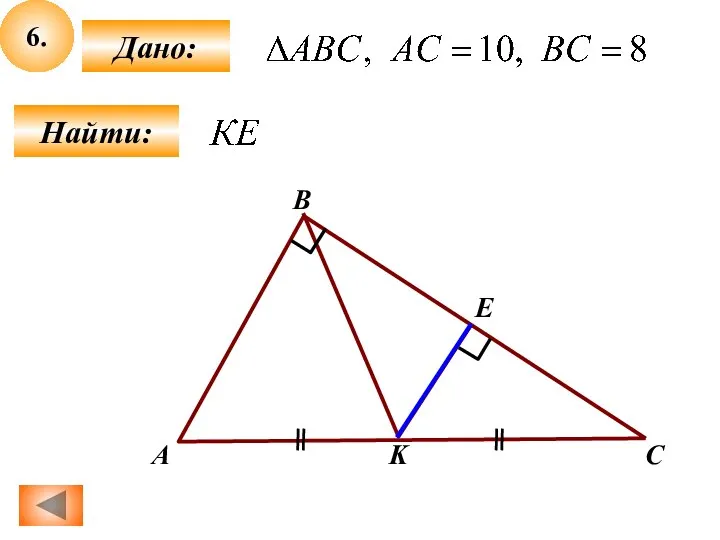 Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля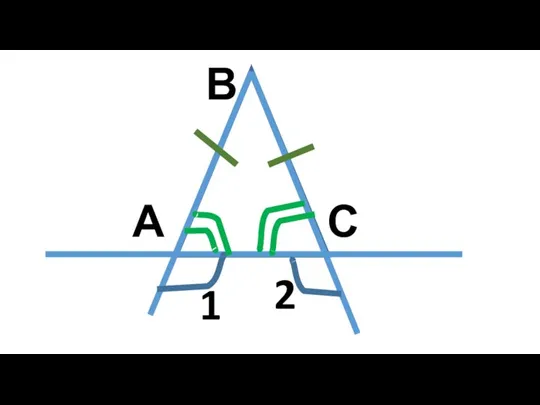 Равнобедренный треугольник
Равнобедренный треугольник Уравнения. 3 класс
Уравнения. 3 класс