Содержание
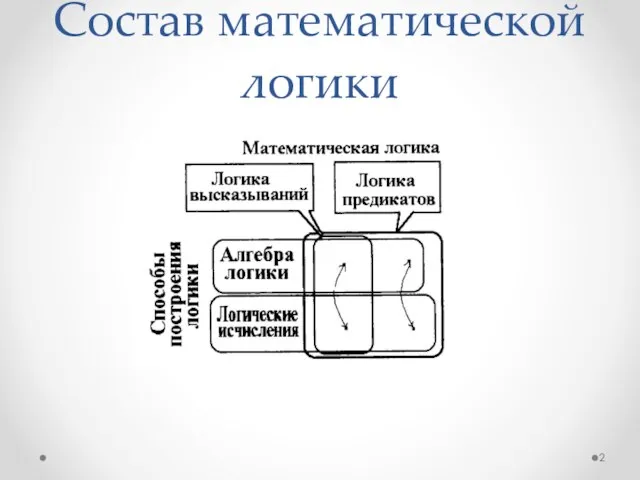
- 2. Cостав математической логики
- 3. Высказывания Из данных предложений выберите те, которые являются высказываниями: Здравствуй! Заяц белый или серый . Этот
- 4. Пример. "Икс любит кашу" Если вместо неизвестного Икс подставить, например Маша, либо Даша, либо Саша, то
- 5. Р(х)=«Икс любит кашу» – одноместный предикат. М={Маша, Даша, Саша} Предметная область Предметные переменные Примеры предикатов Пусть
- 6. Определение 1. Одноместным предикатом Р(х) называется всякая функция одного переменного, аргумент x которой определен на некотором
- 7. Примеры одноместных предикатов Р1(х)=«x – простое число» - одноместный предикат. Пусть МР1- натуральные числа от 2
- 8. Двухместный предикат Пусть N - множество натуральных чисел. Рассмотрим предикат G(x,y): «х Тогда, например, G(l,3) =
- 9. Пусть предметные множества L – {Маша, Саша} – люди, B – {каша, борщ, солянка} Рассмотрим предикат
- 10. Определение 2. Двухместным предикатом P(x,у) называется функция двух переменных х и у, определённая на множестве М=М1×М2
- 11. Пусть Q(x,у) – «х = у», М=R˟R. F(x,у) – «х || у» - прямая х параллельна
- 12. Пример . Среди следующих предложений выделить предикаты и для каждого из них указать область истинности, если
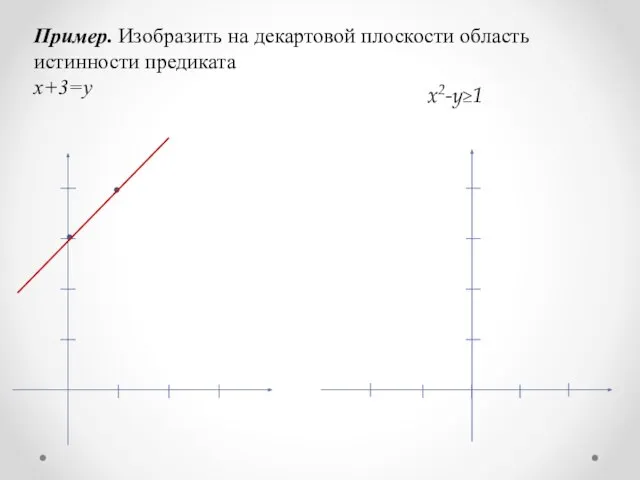
- 13. Пример. Изобразить на декартовой плоскости область истинности предиката x+3=y x2-y≥1
- 14. Определение. Предикатом P(x1, x2, ... , xn) называется функция, аргументы которой определены на некоторых множествах М1,M2,M3,..Mn
- 15. P(x,y): 2(x+y)=2y+2x Q(x): x+1=x F(x,y): x+y=5 Виды предикатов Выполняется для всех х и у – тождественно-истинный
- 16. Предикат называется тождественно истинным, если на всех наборах своих переменных принимает значение 1 (Ip= M). Предикат
- 17. Примеры. Р(х)- «В месяце х температура воздуха в Ярославле не опускается ниже 0 уже 100 лет».
- 18. Логические операции над предикатами
- 19. Логические операции над высказываниями
- 20. Пример. Пусть на некотором множестве М – натуральные числа определены предикаты P(x) и Q(x): P(x): “x
- 21. Пусть на некотором множестве М определены два предиката Р(х) и Q(х). Определение. Конъюнкцией двух предикатов Р(х)
- 22. Дизъюнкция предикатов Пример. Пусть на некотором множестве М – натуральные числа определены предикаты P(x) и Q(x):
- 23. Дизъюнкция предикатов Пусть на некотором множестве М определены два предиката Р(х) и Q(х). Определение. Дизъюнкцией двух
- 24. Изобразить на декартовой плоскости область истинности предиката: ((х+5>0)&(x ((х+5>0) v (y ((х-1>0) v (y=4)) ((х-1>0) &
- 25. Изобразить на декартовой плоскости область истинности предиката
- 26. Изобразить на декартовой плоскости область истинности предиката
- 27. Пример. Пусть на некотором множестве М – натуральные числа определен предикат P(x):“x – четное число” Тогда
- 28. Пусть на некотором множестве М определен предикат Р(х). Определение. Отрицанием предиката Р(х) называется новый предикат Р(х),
- 29. Импликация предикатов Пример. Пусть на некотором множестве М – натуральные числа определены предикаты P(x) и Q(x):
- 30. Пусть на некотором множестве М определены два предиката Р(х) и Q(х). Определение. Импликацией предикатов Р(х) и
- 31. При выполнении логических операций над предикатами к ним применимы и равносильности алгебры логики. Эквиваленция предикатов Пусть
- 32. Изобразите на координатной прямой или координатной плоскости множества истинности следующих предикатов: а) (х > 2) ∧
- 33. Тест Состоит из 7 вопросов. Правильный вариант ответа может быть не один.
- 34. 3. Пусть даны предикаты Р(х): «х - четное число» и Q(х): «х кратно 4», определенные на
- 35. 4. Пусть даны предикаты Р(х): «х - четное число» и Q(х): «х кратно 4», определенные на
- 36. 6. Если значения х,у принадлежат отрезку [2;5], то в списке выражений укажите тождественно ложные предикаты: 1)
- 37. Критерии оценивания За каждый правильный ответ начисляется 1 балл
- 38. 1. Пусть даны предикаты Р(х): «х - четное число» и Q(х): «х кратно 3», определенные на
- 39. Примеры предикатов, определенных на множестве натуральных чисел N2
- 43. Определение. Предикат Q следует из предиката Р, заданного над теми же множествами, что и предикат Q
- 44. Следование и равносильность предикатов
- 45. Определите, являются ли равносильными предикаты, заданные на множестве действительных чисел R
- 46. Кванторные операции над предикатами
- 47. Определение. Операцией связывания квантором общности называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве
- 48. Определение. Операцией связывания квантором существования называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве
- 49. «Выгул кошек и собак воспрещен» K(x): х-кошка C(x): х-собака B(x): для х выгул разрешен ¬∃x((K(x)∨C(x))∧B(x)) ∀x((K(x)∨C(x))→¬B(x))
- 50. Примеры его которого кто-то
- 51. Примеры «существует натуральное х, большее 1» - истинное высказывание. «для любого х число х является делителем
- 52. Связанные и свободные переменные Определение. Присоединение квантора с переменной к предикатной формуле называется навешивание квантора на
- 53. Навешивание кванторов на двухместный предикат
- 54. Одноименные кванторы можно менять местами, что не влияет на истинность высказывания. Например: (∃у) (∃х) (х +
- 55. Для доказательства истинности утверждения (∀х) Р(х) с квантором общности, определенного на множестве М, необходимо убедиться в
- 56. Высказывание ∃x P(x) истинно, если можно указать такое значение а∊М при котором Р(х) обращается в истинное
- 57. Упражнения
- 58. Выяснить, какие из следующих предложений являются высказываниями, а какие предикатами: а) найдется такое х, что х+
- 59. Записать
- 60. На языке логики предикатов записать определение убывающей функции Функция f(x) называется убывающей а множестве M, если
- 61. Домашнее задание 1. Записать словами формулу где, A(x) = “x – студент”; B(y) = “y –
- 62. Найти формулу соответствующую предложению. “По меньшей мере один объект обладает свойством Р”. Ответы: Упражнения Найти формулу
- 63. Формулы логики предикатов. Равносильность формул Определение. Формула логики предикатов определяется индуктивно следующим образом: 1. Любая формула
- 64. Являются ли формулами следующие выражения а) A & B → C, где A, B, C –
- 65. Пример. 1. Следующие выражения являются формулами логики предикатов: а) A & B → C, где A,
- 66. Определение. Формулы F и G, определенные на некотором множестве М, называются равносильными на этом множестве, если
- 67. Являются ли равносильными предикаты: а) P(x): (3x+8)/(x2+1)=0 и Q(z): -6z-16=0 б) P(x):(x+2)(x-3)=0 и Q(x): (x-3)=0 На
- 68. Переход от одних формул к равносильным им другим формулам логики предикатов может быть произведен по следующим
- 69. 3. Вынос квантора за скобки. Пусть формула A(x) содержит переменную x, а формула B не содержит
- 70. 5. Перестановка одноименных кванторов. ∀x∀yA(x,y) ≡∀y∀xA(x,y). ∃x∃yA(x,y) ≡∃y∃xA(x,y). Разноименные кванторы переставлять, вообще говоря, нельзя!
- 71. Следствия и равносильности логики предикатов
- 72. Приведенные и нормальные формулы Определение. Формулы, в которых из логических символов имеются только символы &, V
- 73. Существуют две задачи, определяющие связь между суждениями и формулами логики предикатов: 1) выражение суждения в виде
- 74. Все атрибутивные суждения можно разделить на следующие типы: Атрибутивные суждения Если кванторная переменная связана квантором общности
- 75. а) Веста – собака. Заменим имя "Веста" символом "в" и введем предикат P(x) = "x –
- 76. б) Всякая логическая функция может быть задана таблицей. Введем предикаты: S(x) = "x – логическая функция";
- 77. в) Ни один народ не хочет войны. Введем предикаты: S(x) = "x – народ"; P(x) =
- 78. г) Некоторые журналисты были в космосе. Введем предикаты: S(x) = "x – журналист"; P(x) = "x
- 79. д) Некоторые современники динозавров не вымерли. Введем предикаты: S(x) = "x – современник динозавров"; P(x) =
- 80. Язык логики предикатов удобен для записи математических предложений: определений, теорем, необходимых и достаточных условий. Пример. Теорема
- 82. Скачать презентацию
































![6. Если значения х,у принадлежат отрезку [2;5], то в списке выражений укажите](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/850639/slide-35.jpg)












































 Планиметрия. Стереометрия
Планиметрия. Стереометрия Правильные многоугольники
Правильные многоугольники Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Урок математики в 1 классе
Урок математики в 1 классе Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Решение квадратного уравнения общего вида
Решение квадратного уравнения общего вида Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Уравнения математической физики
Уравнения математической физики Интегральные уравнения
Интегральные уравнения Критерий Манна-Уитни
Критерий Манна-Уитни Ребусы от тётушки Совы
Ребусы от тётушки Совы Уравнения – это ключ, открывающий все математические сезамы. С.Коваль
Уравнения – это ключ, открывающий все математические сезамы. С.Коваль Соединения с повторениями
Соединения с повторениями Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  формулы сокрощенного умножения
формулы сокрощенного умножения Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест
Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест Упрощение выражений. Тест
Упрощение выражений. Тест Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат В мире цифр. Дидактическое пособие
В мире цифр. Дидактическое пособие Состав чисел первого десятка
Состав чисел первого десятка Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Тригонометрические уравнения
Тригонометрические уравнения Правильные многоугольники
Правильные многоугольники Презентация на тему ГИА 2013. Модуль алгебра №6
Презентация на тему ГИА 2013. Модуль алгебра №6  Сложение, вычитание, умножение,
Сложение, вычитание, умножение,