Нормальное распределения случайной величины. Функция Лапласа

Нормальное распределение наиболее часто встречается на практике и теоретически наиболее полно разработано. Множество событий происходит случайно вследствие воздействия на них большого числа независимых (или слабо зависимых) возмущений, и у таких явлений закон распределения близок к нормальному. Установлено, что нормальное распределение содержит минимум информации о случайной величине по сравнению с любыми распределениями с той же дисперсией. Следовательно, замена некоторого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений, что широко используется на практике.

График плотности нормального распределения
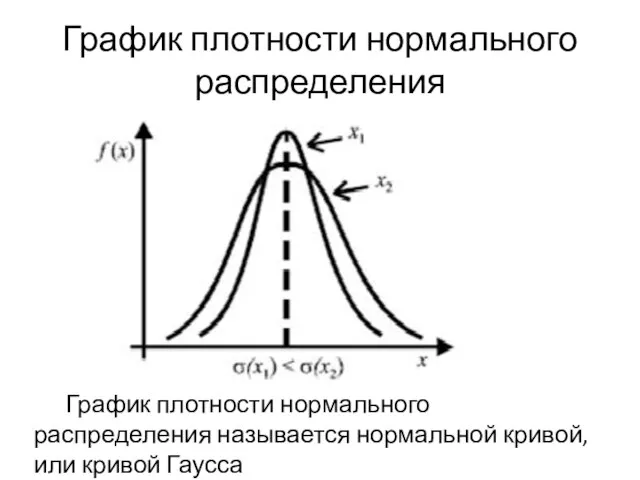
График плотности нормального распределения называется нормальной кривой, или кривой Гаусса

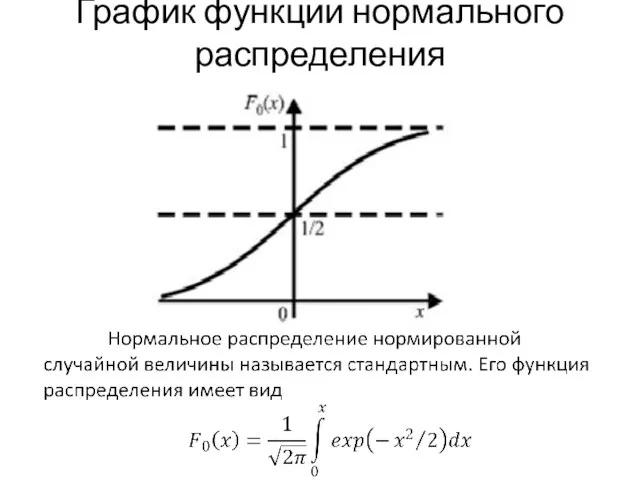
График функции нормального распределения

функция Лапласа