Содержание
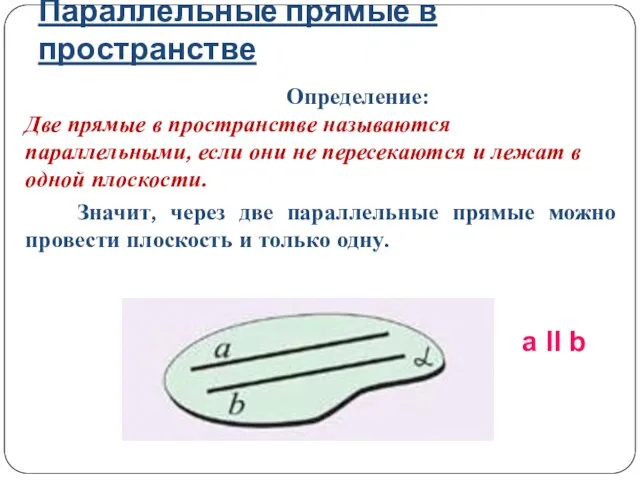
- 2. Параллельные прямые в пространстве Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и
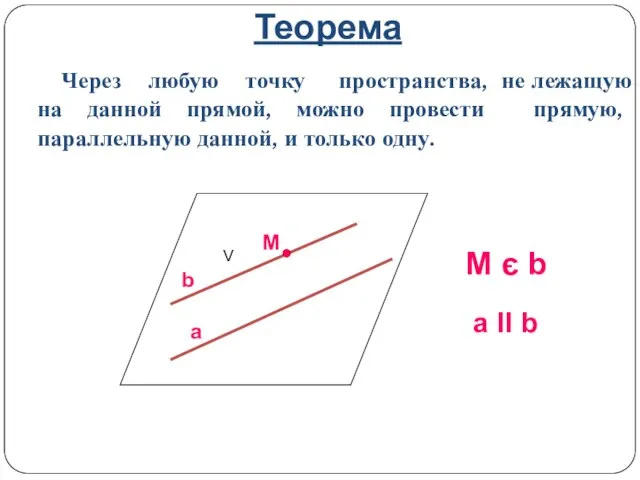
- 3. Теорема Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и
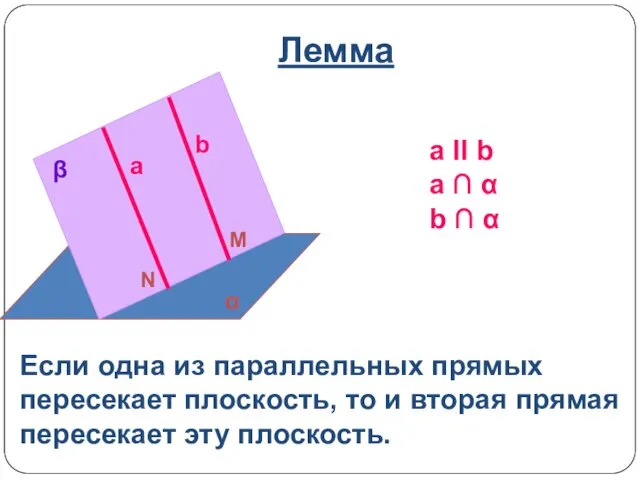
- 4. Лемма a ΙΙ b a ∩ α b ∩ α Если одна из параллельных прямых пересекает
- 5. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ
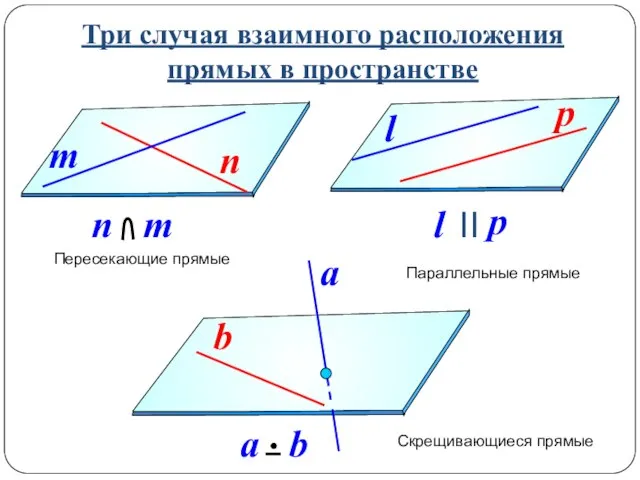
- 6. Три случая взаимного расположения прямых в пространстве Пересекающие прямые Параллельные прямые Скрещивающиеся прямые
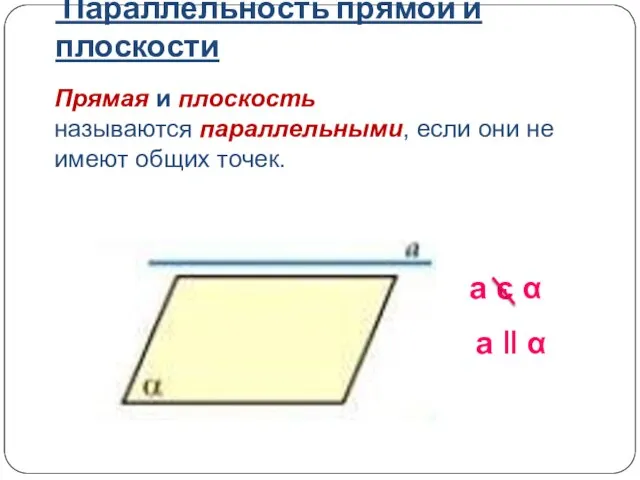
- 7. Прямая и плоскость называются параллельными, если они не имеют общих точек. a є α a ǁ
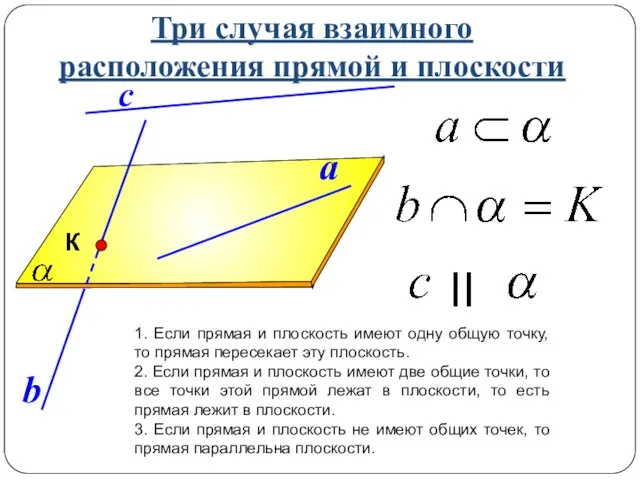
- 8. Три случая взаимного расположения прямой и плоскости 1. Если прямая и плоскость имеют одну общую точку,
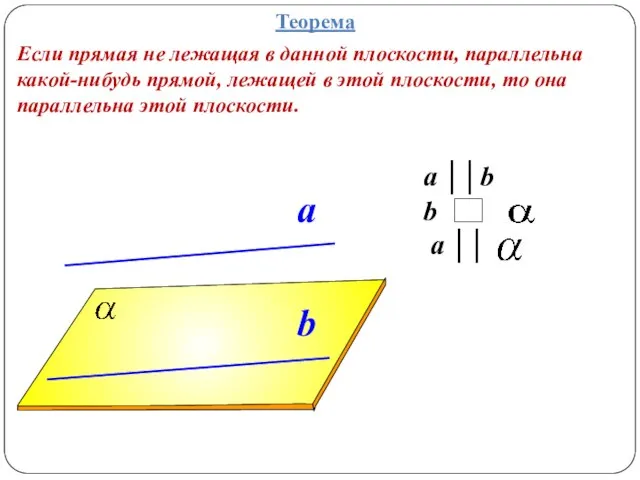
- 9. a ││b b a ││ a b Теорема Если прямая не лежащая в данной плоскости, параллельна
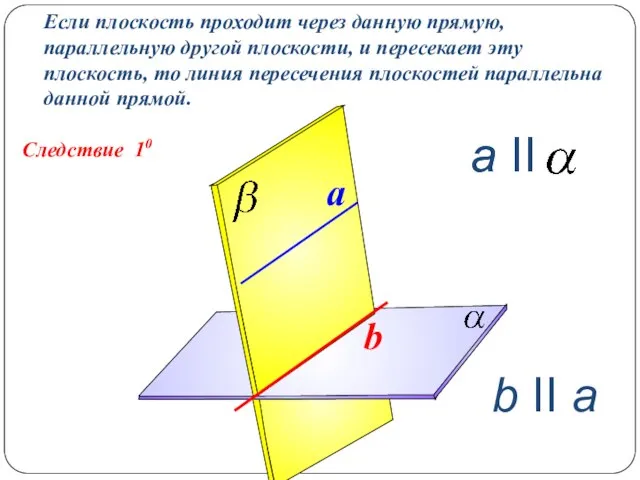
- 10. Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то
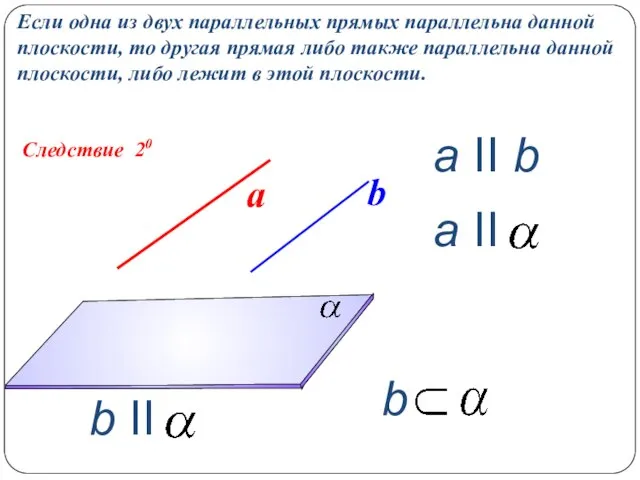
- 11. Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также
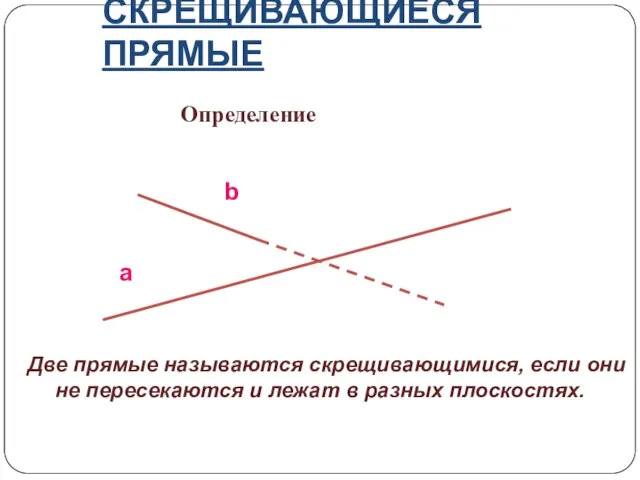
- 12. СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Определение a b Две прямые называются скрещивающимися, если они не пересекаются и лежат в
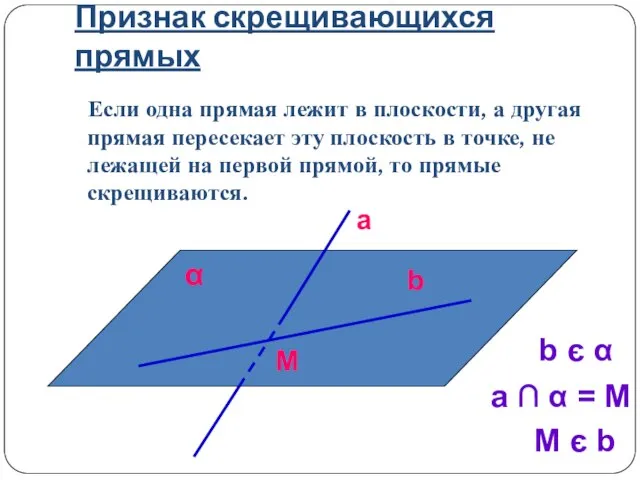
- 13. Признак скрещивающихся прямых Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в
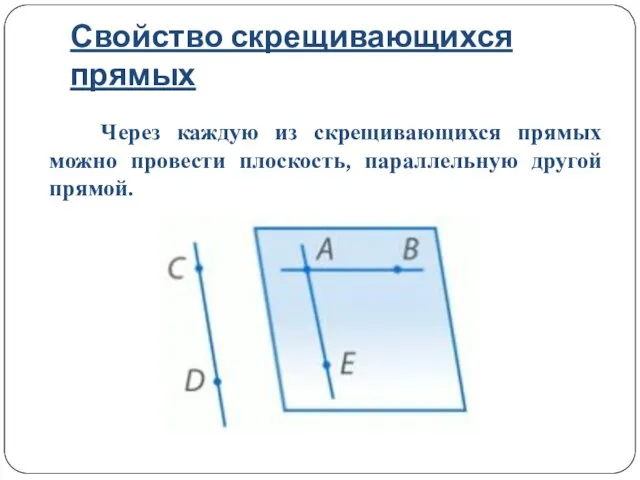
- 14. Свойство скрещивающихся прямых Через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
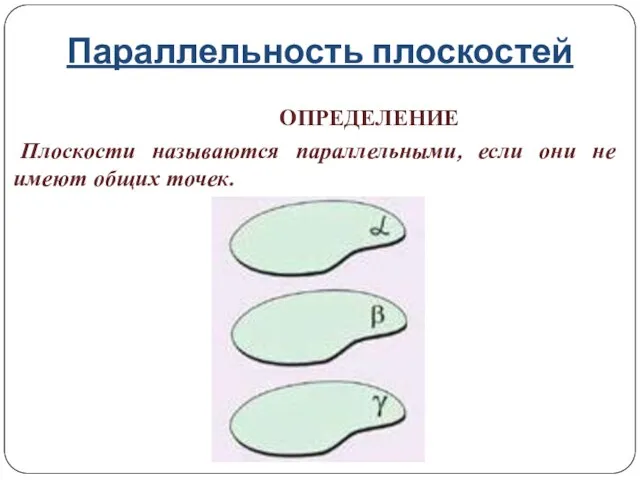
- 15. Параллельность плоскостей ОПРЕДЕЛЕНИЕ Плоскости называются параллельными, если они не имеют общих точек.
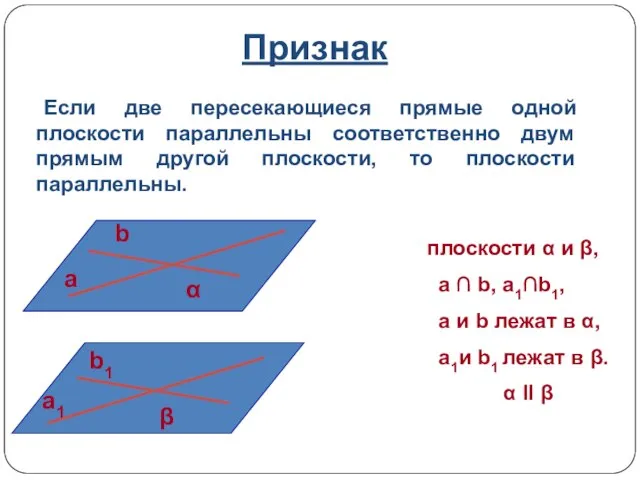
- 16. Признак плоскости α и β, a ∩ b, a1∩b1, a и b лежат в α, a1и
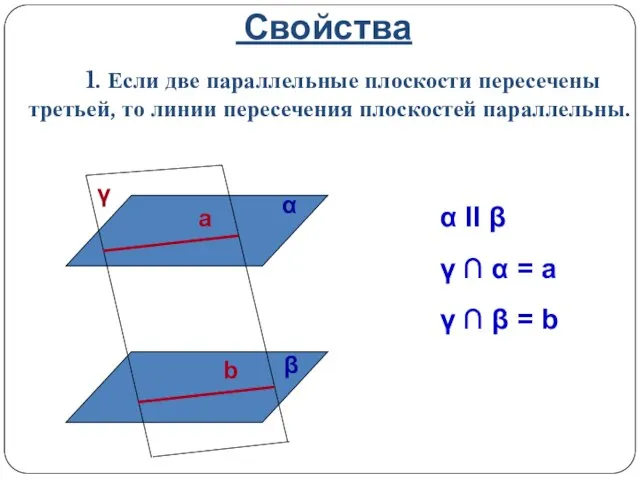
- 17. Свойства 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. α II β
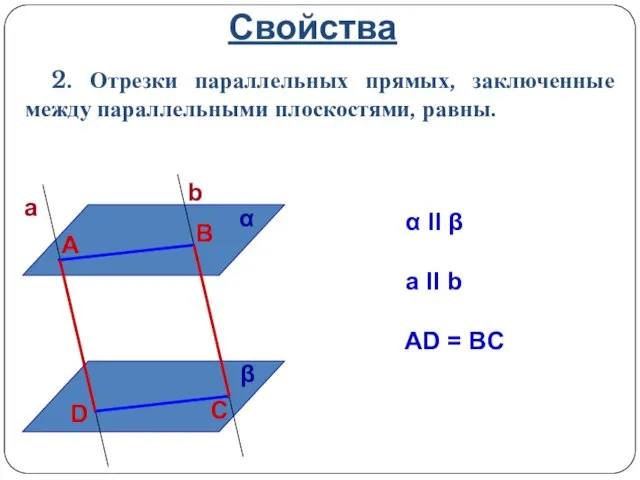
- 18. Свойства 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. α II β a II b
- 20. Скачать презентацию

 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Тест. Равенство треугольников
Тест. Равенство треугольников Логарифм числа
Логарифм числа Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сложение с числом 10
Сложение с числом 10 Линейная корреляция
Линейная корреляция Проецирование – это процесс получения
Проецирование – это процесс получения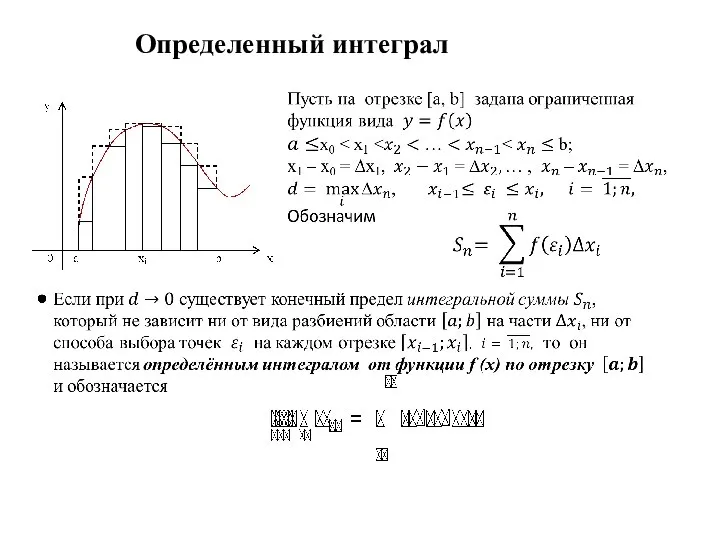 Определённый интеграл
Определённый интеграл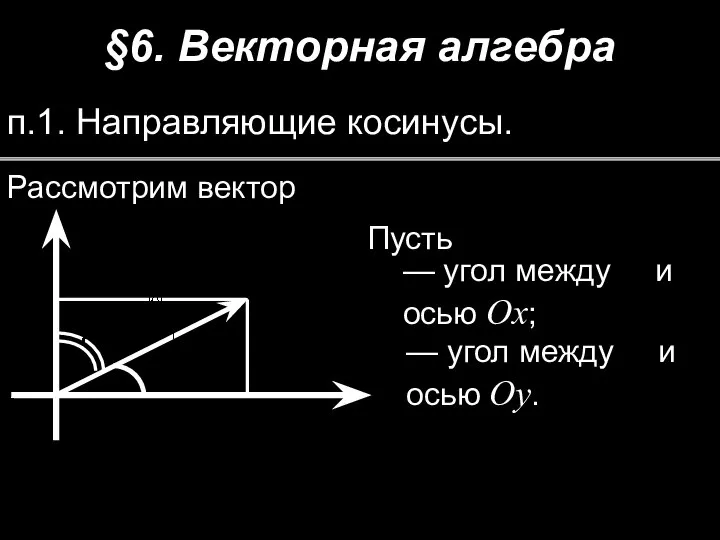 2.3. Векторная алгебра
2.3. Векторная алгебра Признаки параллельности прямых
Признаки параллельности прямых Решение задач. Урок математики
Решение задач. Урок математики Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Подготовка к ЕГЭ
Подготовка к ЕГЭ Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Лекция 5. Трехмерные преобразования
Лекция 5. Трехмерные преобразования Кратные чисел. 5 класс
Кратные чисел. 5 класс 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Pervoobraznaya
Pervoobraznaya Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм Решение треугольников
Решение треугольников Треугольник. Виды треугольников
Треугольник. Виды треугольников Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Иррациональные числа
Иррациональные числа Тест 3 по математике
Тест 3 по математике