Исследование функций

Что называется числовой функцией?
Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х.
2. Что называется графиком функции?
Графиком функции f называется множество всех точек (х;у) координатной плоскости, где у=f(х), а х «пробегает» всю область определения функции f.
Вопросы:

3. Какие из линий, изображённых на
рисунке являются графиками функций?

Вопросы:
Графиком функции у = х2 является …
Вертикальную координатную прямую на
координатной плоскости называют осью…
3. Графиком функции у = 1/х является …
4. Зависимость, при которой каждому значению х ставится в соответствие единственное значение у называется …
5. Множество всех точек (х;у) координатной плоскости, где у = f(х), а х «пробегает» всю область определения функции f.
6. Графиком функции у = кх + в является …
7. Горизонтальную координатную прямую на координатной плоскости называют осью…
8. Ось х и ось у называют осями …
г
р
а
а
а
а
а
а
п
п
ф
ф
р
б
о
л
и
к
р
р
б
л
о
г
о
о
к
и
и
с
с
с
п
е
я
м
я
д
и
н
б
ц
к
р
д
и
н
т
у
ц
я
т
1
2
3
4
6
5
7
8
Кроссворд

Схема исследования функций:
1. Найти область определения функции.
2. Определить чётность или нечётность функции, периодичность.
3. Найти координаты точек пересечения графика с осями координат.
1. Найти промежутки знакопостоянства функции.
5. Определить промежутки возрастания или убывания функции.
6. Найти точки экстремума функции, вид экстремума (максимум или минимум) и значения функции в этих точках.
7. Найти область значений функции.
8. Построить график функции.

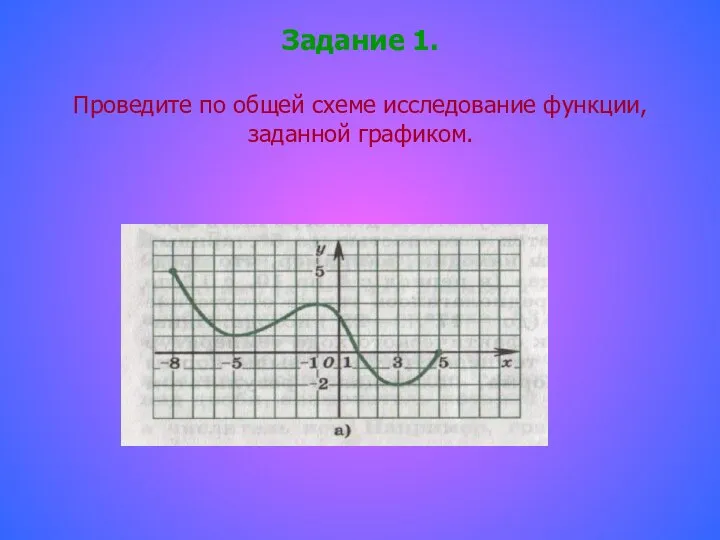
Задание 1.
Проведите по общей схеме исследование функции,
заданной графиком.

1. Область определения функции D(у) =[-8; 5].
2. Функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью ОХ: (1; 0), (5; 0).
с осью ОУ: (0; 2).
1. Промежутки знакопостоянства:
f(х) > 0, при х принадлежащем промежутку [-8; 1).
f(х) < 0, при х принадлежащем промежутку (1; 5].
5. Функция возрастает на промежутке [-5; -1]U[3; 5].
Функция убывает на промежутке [-8; -5]U[-1; 3].
6. Точки экстремума: хmax=-1, уmax= 3, хmin= -5, уmin= 1,
хmin= 3, уmin= -2.
7. Область значений Е(у) = [-2; 5].

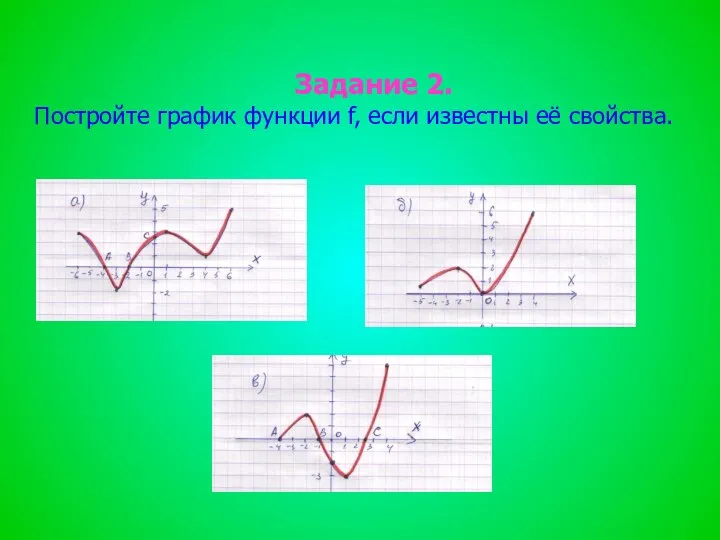
Задание 2.
Постройте график функции f, если известны её свойства.

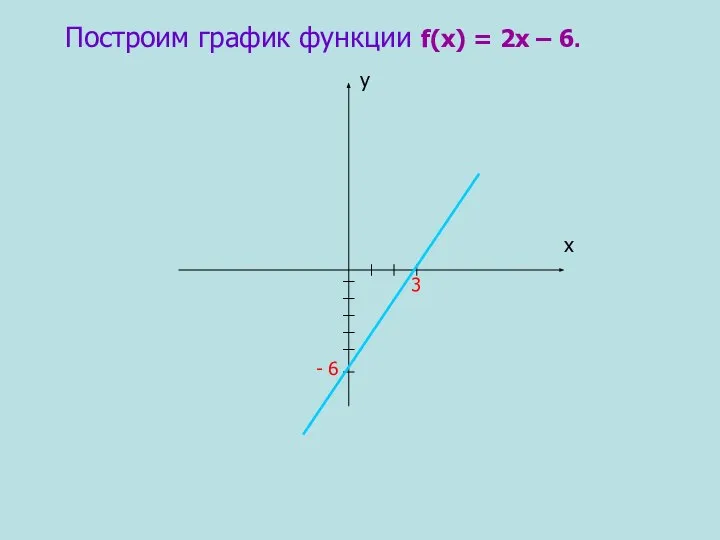
Задание 1. Построить график функции
f(х) = 2х – 6, используя схему исследования.

Исследование функции f(х) = 2х – 6.
Область определения функции D(у) =(-∞; +∞).
2. f(- х) = 2(-х) – 6 = – 2х – 6 = -(2х + 6) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
2х – 6 = 0, 2· 0 – 6 = у,
2х = 6, 0 – 6 = у,
х = 3 у = - 6.
(3; 0). (0; -6).
4. Промежутки знакопостоянства:
f(х) > 0, 2х - 6 > 0, 2х > 6, х > 3. (3; +∞).
f(х) < 0, 2х – 6 < 0, 2х < 6, х < 3. (-∞; 3).
5. Функция возрастает на промежутке (-∞; +∞), т. к. к =2, к> 0.
6. Точек экстремума нет.
7. Область значений Е(у) = (-∞; +∞).

Построим график функции f(х) = 2х – 6.
3
- 6
х
у

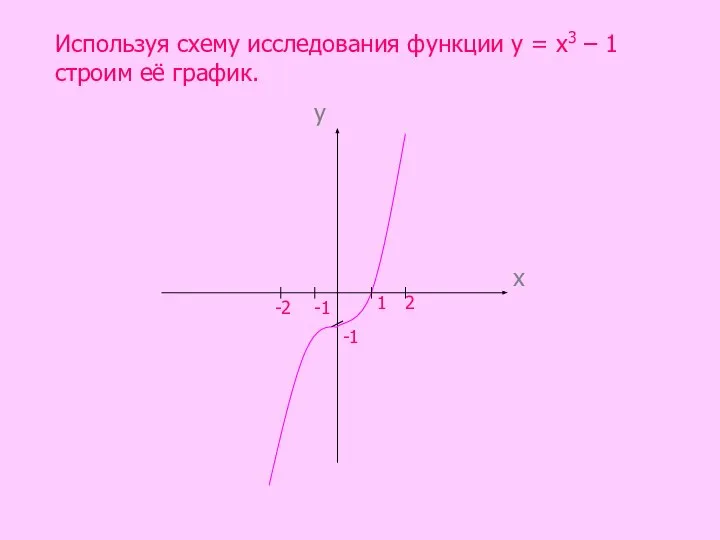
Задание 2.
Построить график функции f(х) = х3 – 1,
используя схему исследования.

Исследуем функцию у = х3 – 1
1. Область определения функции D(у) =(-∞; +∞).
2. f(- х) = (-х)3 – 1 = – х3 – 1 = -(х3 + 1) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
х3 – 1 = 0, у = 03 – 1,
х3 = 1, у = - 1.
х = 1. (0; -1).
(1; 0).
4. Промежутки знакопостоянства:
f(х) > 0, х3 - 1 > 0, х3 > 1, х > 1. (1; +∞).
f(х) < 0, х3 – 1 < 0, х3 < 1, х < 1. (-∞; 1).

5. х2 = 1, х1 = 0.
f(х2) = f(1) = 13 – 1 = 0.
f(х1) = f(0) = 03 – 1 = -1.
х2 > х1, f(х2) > f(х1) – функция возрастает.
6. Точек экстремума нет, т. к. функция возрастает на всей области определения.
7. Область значений Е(у) = (-∞; +∞).

Используя схему исследования функции у = х3 – 1
строим её график.
х
у
1
-1
2
-1
-2

Сделаем вывод.
Графиком функции у = х3 – 1
является кубическая парабола, опущенная на 1 единицу вниз.

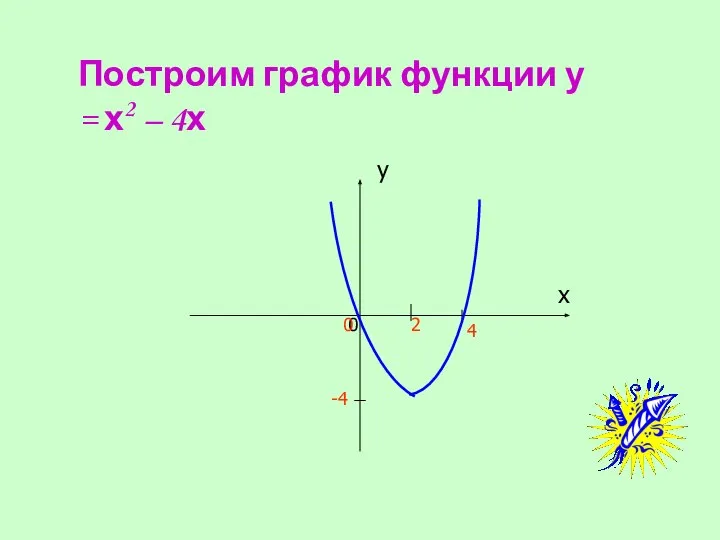
Задание 3.
Построить график функции f(х) = х2 – 4х,
используя схему исследования.

Исследуем функцию у = х2 – 4х
1. Область определения функции D(у) =(-∞; +∞).
2. f(- х) = (-х)2 – 4(-х) = х2 + 4х = -(-х2 – 4х) – функция ни чётная, ни нечетная. Функция не периодическая.
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
х2 – 4х = 0, у = 02 - 4 · 0 = 0,
х(х – 4) = 0, у = 0.
х = 0 или х- 4 = 0 (0; 0)
х = 4.
(0; 0). (4; 0).
Найдём вершину параболы: х = 4 : 2 = 2;
у = 22 - 4· 2 = 4 – 8 = - 4.
(2; -4) – вершина параболы.

4. Промежутки знакопостоянства:
f(х) > 0, х2 – 4х > 0, х(х -4) > 0,
Х2 – 4х = 0, х(х -4) = 0,
х = 0 или х- 4 = 0.
х = 4.
f(х) > 0, ( -∞; 0)U(4; +∞).
f(х) < 0, (0; 4).
0
4
−
+
+
х

5. Промежутки возрастания и убывания функции:
х2 = 1, х1 = 0. f(х2) = f(1) = 12 – 4·1 = -3.
f(х1) = f(0) = 02 – 4·0 = 0.
х2 > х1, f(х2) < f(х1) – функция убывает на промежутке (- ∞;2).
х1 = 3, х2 = 4.
f(х1) = f(3) = 32 – 4·3 = -3.
f(х2) = f(4) = 42 – 4·4 = 0.
х2 > х1, f(х2) > f(х1) – функция возрастает на промежутке (2; +∞).
6. Точка минимума (2; -4).
7. Область значений Е(у) = (-4; +∞).

Построим график функции у = х2 – 4х
2
0
0
-4
4
х
у

Вывод
Графиком функции у = х2 – 4х
является парабола,
ветви параболы направлены вверх.

Самостоятельно выполнить задание.
Построить график функции
f(х) = √х – 3,
используя схему исследования.

Исследуем функцию f(х) = √х – 3 по схеме исследования.
1. Область определения функции D(у) =[ ).
2. f(- х) =
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
4. Промежутки знакопостоянства:
f(х) > 0,

Промежутки возрастания и убывания функции:
х2 = 4, х1 = 3.
f(х2) = f(4) =
f(х1) = f(3) =
6. Точек экстремума
7. Область значений

Используя схему исследования
функции f(х)= √х – 3 построим её график.
х
у
3

Задание 5.
Построить график функции f(х) = |х| + 1,
используя схему исследования.

Исследуем функцию f(х) = |х| + 1
1. Область определения функции D(у)
2. f(- х) =
3. Пересечение с осью:
а) с осью ОХ, у = 0. б) с осью ОУ, х = 0.
4. Промежутки знакопостоянства:
f(х) > 0,

5. Промежутки возрастания и убывания функции:
х2 = -1, х1 = -2.
х1 = 1, х2 = 2.
6. Точка минимума
7. Область значений Е(у) =

Построим график функции f(х) = |х| + 1
х
у
1