Содержание
- 2. Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
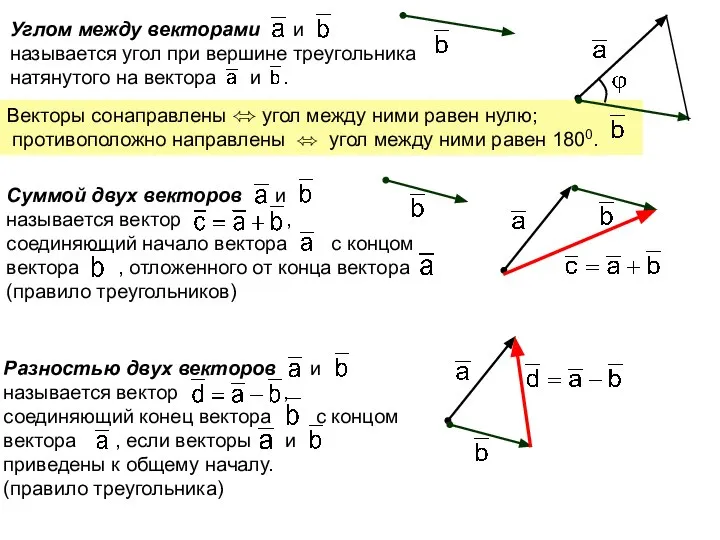
- 3. Векторы сонаправлены ⬄ угол между ними равен нулю; противоположно направлены ⬄ угол между ними равен 1800.
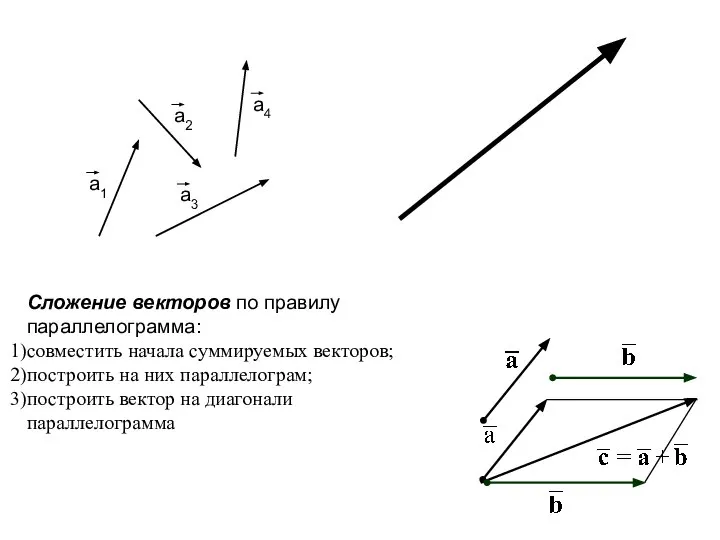
- 4. Сложение векторов по правилу параллелограмма: совместить начала суммируемых векторов; построить на них параллелограм; построить вектор на
- 5. и направление вектора , если λ > 0; вектора , если λ Из определения суммы: Из
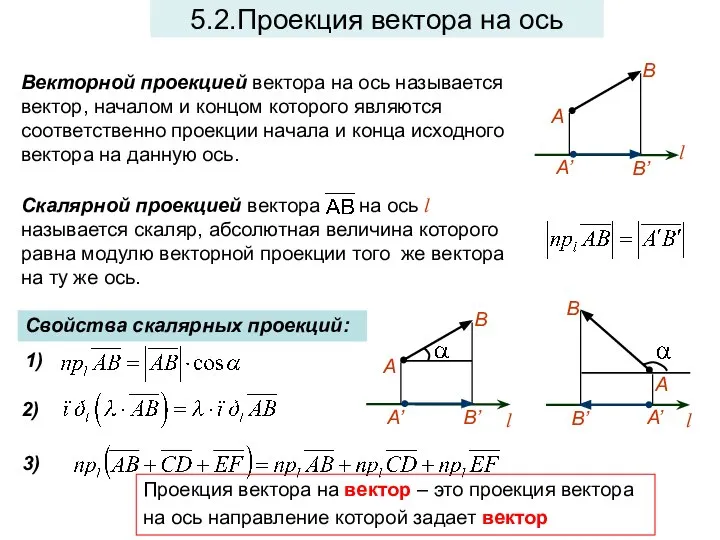
- 6. 5.2.Проекция вектора на ось Векторной проекцией вектора на ось называется вектор, началом и концом которого являются
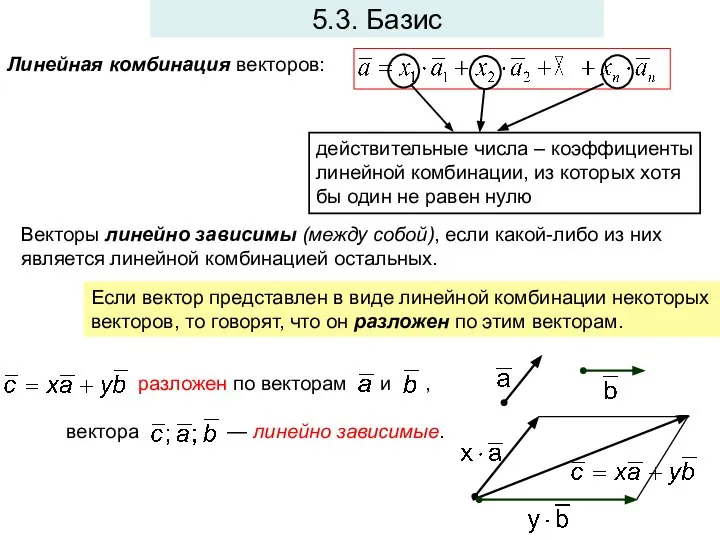
- 7. 5.3. Базис Векторы линейно зависимы (между собой), если какой-либо из них является линейной комбинацией остальных. Если
- 8. Два вектора линейно зависимы ⬄ коллинеарны Совокупность двух линейно независимых векторов лежащих в одной плоскости называется
- 9. 5.4. Декартова прямоугольная система координат Базис называется ортонормированным, если его вектора единичны и взаимно перпендикулярны: Плоскости,
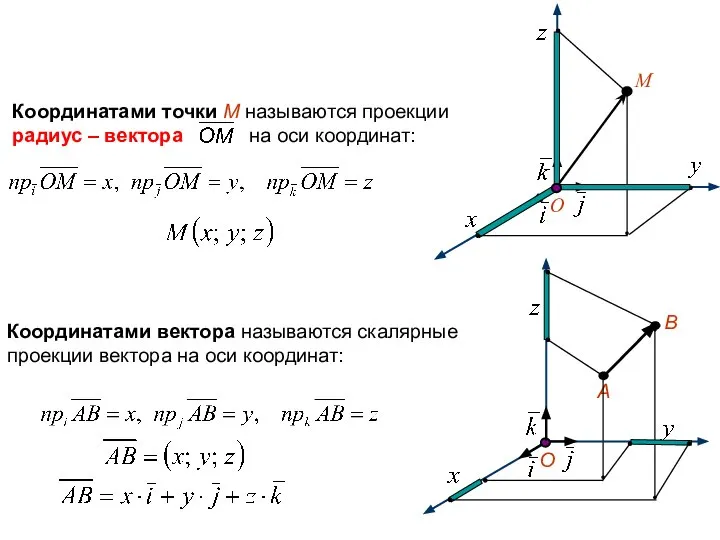
- 10. Координатами вектора называются скалярные проекции вектора на оси координат:
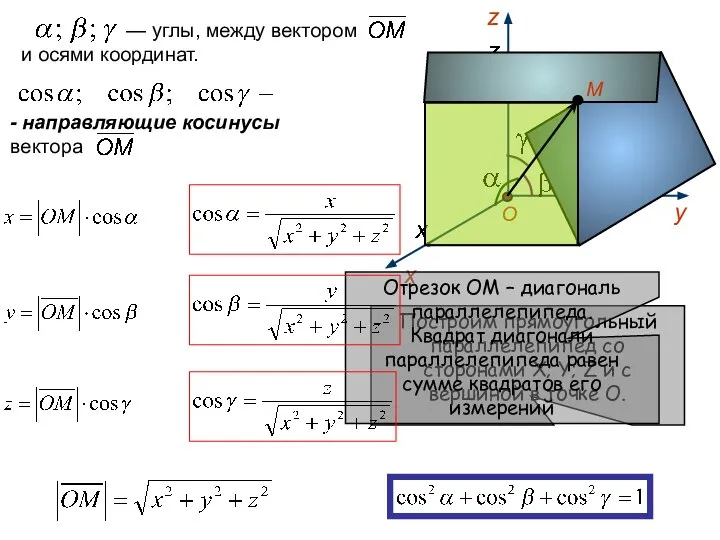
- 11. Построим прямоугольный параллелепипед со сторонами X; Y; Z и с вершиной в точке О. Отрезок ОМ
- 12. Операции над векторами в декартовой системе координат По свойствам скалярной проекции вектора на ось получим: По
- 13. Найти модуль и орт суммы векторов: ПРИМЕР
- 15. Скачать презентацию






 Возведение в квадрат суммы и разности двух выражений. Тест
Возведение в квадрат суммы и разности двух выражений. Тест Презентация на тему Число 0 Цифра 0
Презентация на тему Число 0 Цифра 0  54 задачи на чертежах по планиметрии. Теорема Пифагора
54 задачи на чертежах по планиметрии. Теорема Пифагора Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс
Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс  Я тебя слышу
Я тебя слышу Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Великие математики
Великие математики Преобразование выражений с помощью формул сокращенного умножения
Преобразование выражений с помощью формул сокращенного умножения Производная функции
Производная функции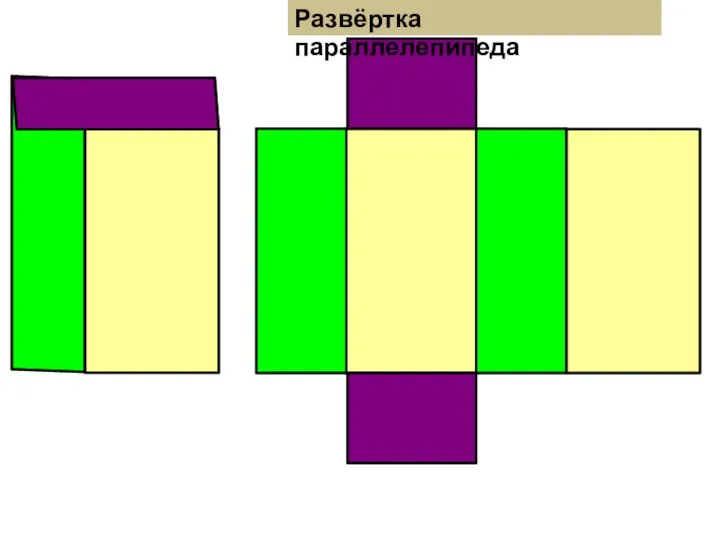 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1)
TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1) Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Нахождение угла между прямой и плоскостью
Нахождение угла между прямой и плоскостью Математико-картографическое моделирование
Математико-картографическое моделирование Презентация на тему Квадратный дециметр (3 класс)
Презентация на тему Квадратный дециметр (3 класс)  Шар и сфера
Шар и сфера ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум
ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс
Успешный ОГЭ: решаем устно. Урок геометрии, 9 класс Легенды о Пифагоре и его теореме
Легенды о Пифагоре и его теореме Математический диктант. Шаблон проверки
Математический диктант. Шаблон проверки Ряды распределения
Ряды распределения Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок
Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Ознакомление с понятием сантиметр
Ознакомление с понятием сантиметр