Слайд 2Рекомендуемая литература:
1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] : Учебники
![Рекомендуемая литература: 1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1022031/slide-1.jpg)
— Электрон. дан. — М. : Омега-Л, 2010. — 410 с. — Режим доступа: http://e.lanbook.com/book/5534 . Раздел «Экономика и менеджмент».
2. Годин, А.М. Статистика: Учебник. [Электронный ресурс] : Учебники — Электрон. дан. — М. : Дашков и К, 2011. — 460 с. — Режим доступа: http://e.lanbook.com/book/967 . Раздел «Экономика и менеджмент».
3.Балдин, К.В. Общая теория статистики: Учебное пособие. [Электронный ресурс] : Учебные пособия / К.В. Балдин, А.В. Рукосуев. — Электрон. дан. — М. : Дашков и К, 2010. — 312 с. — Режим доступа: http://e.lanbook.com/book/955 .Раздел «Экономика и менеджмент».
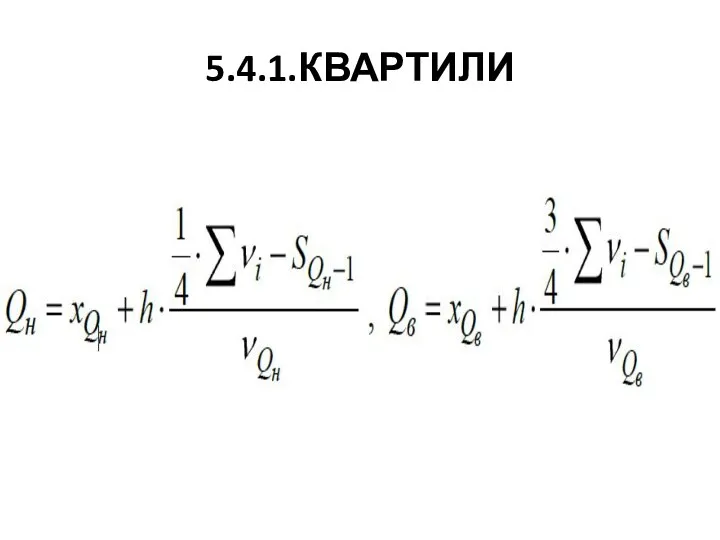
Слайд 35.4.КВАРТИЛИ, КВАРТИЛЬНЫЙ РАЗМАХ
5.4.1 Квартили
Квартили – это значения признака, делящие ранжированную совокупность

на четыре равновеликие части.
Различают:
А.Нижнюю квартиль –Qн;
Б.Среднюю квартиль – медиану;
В.Верхнюю квартиль –Qв.
Слайд 75.3.2.Квартильный размах
Квартильный размах – разница между верхней и нижней квартилями:
Н

= Qв - Qн
Квартильный размах охватывает 50% значений выборки.
Слайд 85.4.КВАРТИЛИ ,КВАРТИЛЬНЫЙ РАЗМАХ
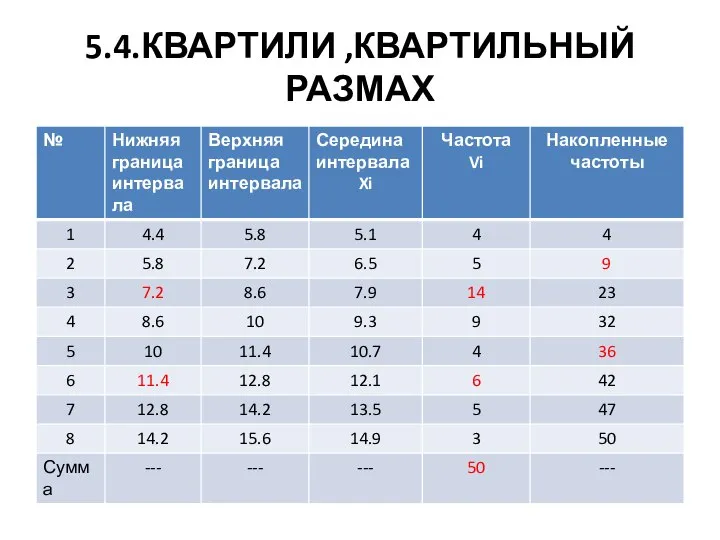
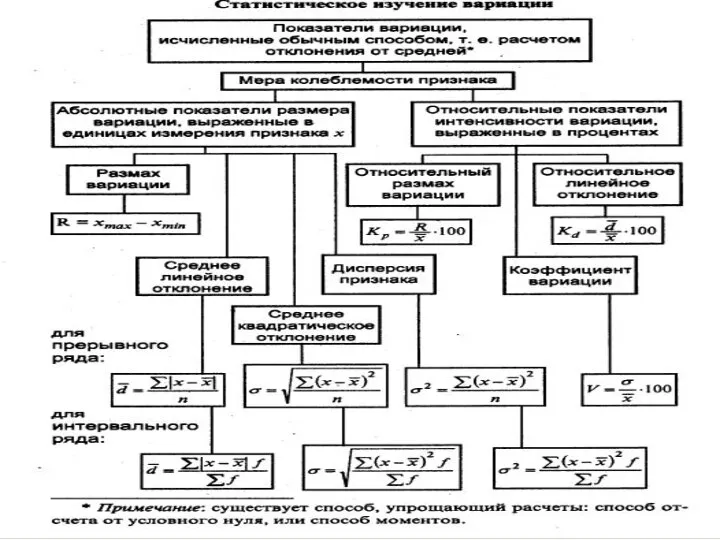
Слайд 96.1. Абсолютные показатели математической оценки размера вариации
Для определения величины вариации применяются

следующие абсолютные показатели вариации:
1.Размах вариации;
2. Среднее линейное отклонение;
3. Дисперсия признака;
4.Среднее квадратическое отклонение.
Слайд 106.1. Абсолютные показатели математической оценки размера вариации
6.1.1.Размах вариации
R = X max

- X min
Слайд 116.1.2. Среднее линейное отклонение
Для ранжированного ряда:
∑ [ Хi - Х]
![6.1.2. Среднее линейное отклонение Для ранжированного ряда: ∑ [ Хi - Х]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1022031/slide-10.jpg)
d = ----------------------- (простое);
N
Для интервального ряда:
∑ [ Хi - Х] V
d = ----------------------- (взвешенное).
∑ V
Слайд 126.1.3. Дисперсия признака
Для ранжированного ряда:
∑ ( Хi - Х )²
σ²

= ----------------------- (простая);
N
Для интервального ряда:
∑ ( Хi - Х )² Vi
σ² = ----------------------- (взвешенная).
∑ V
Слайд 136.1.4. Среднее квадратическое отклонение
Для ранжированного ряда:
∑ ( Хi - Х )²

σ = √---------------------- (простое);
N
Для интервального ряда:
∑ ( Хi - Х )² Vi
σ = √----------------------- (взвешенное).
∑ Vi
Слайд 146.1.4. Среднее квадратическое отклонение
Правило «трех сигм»
- в пределахX ±σ

находится 68,3% вариант;
- в пределах X ± 2σ - 95,4% вариант;
- в пределах X ± 3σ - 99,7%.
Слайд 156.5.Статистическое изучение вариации в прерывных, ранжированных, непрерывных и интервальных рядах
Для дискретного

(прерывного) или ранжированного ряда:
∑ [ Хi - Х]
d = -----------------------;
N
∑ ( Хi - Х )²
σ² = -----------------------;
N
∑ ( Хi - Х )²
σ = √ --------------------
N
Слайд 166.5.Статистическое изучение вариации в прерывных, ранжированных, непрерывных и интервальных рядах
В интервальном

ряду или по сгруппированным данным :
∑ [ Хi - Х] Vi
d = ----------------------;
∑ Vi
∑ ( Хi - Х )²Vi
σ² = -----------------------;
∑ Vi
∑ ( Хi - Х )²Vi
σ = √ ------------------------
∑ Vi
Слайд 176.2.Относительные показатели интенсивности вариации
Существуют три относительных показателя, выраженных в процентах:
1.Относительный размах

вариации;
2. Относительное линейное отклонение ;
3. Коэффициент вариации .
Слайд 18
6.2.1.Относительный размах вариации

Слайд 19
6.2.2. Относительное линейное отклонение

Слайд 226.3.Методика определения среднего квадратического отклонения или дисперсии признака
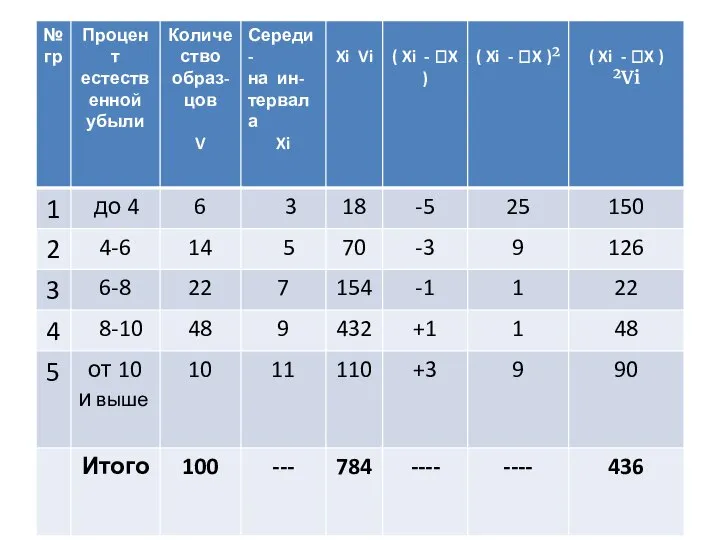
Пример 1. Для изучения

естественной убыли произведено 5%-ное выборочное обследование партии хранящихся на базе товаров. В результате лабораторного анализа установлено распределение образцов.
Рассчитать: средний процент естественной убыли в выборке и среднее квадратическое отклонение или дисперсию
Слайд 23Методика определения среднего квадратического отклонения или дисперсии признака
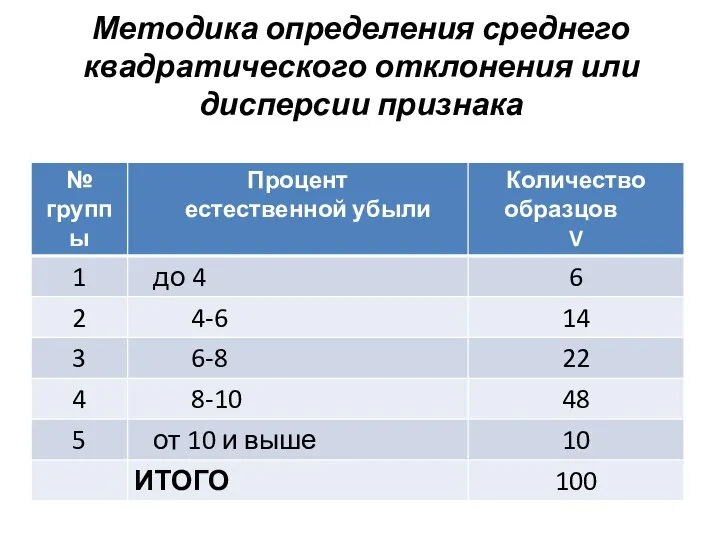
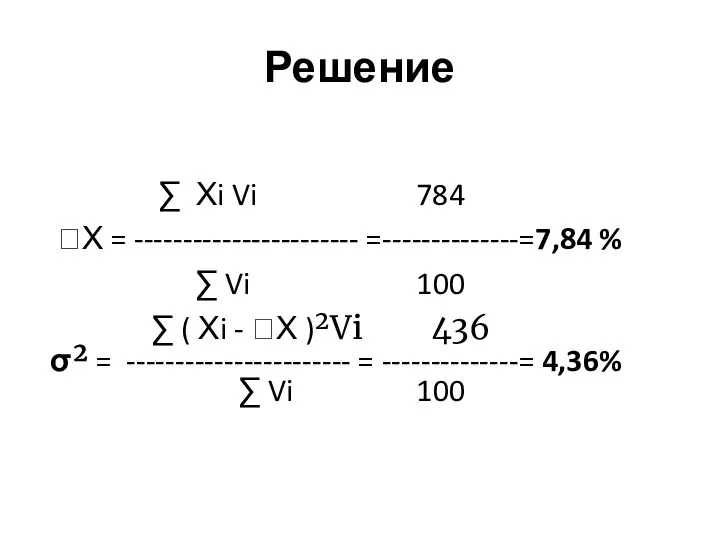
Слайд 25Решение
∑ Хi Vi 784
Х = ----------------------- =--------------=7,84 %
∑
Vi 100
∑ ( Хi - Х )²Vi 436
σ² = ----------------------- = --------------= 4,36%
∑ Vi 100
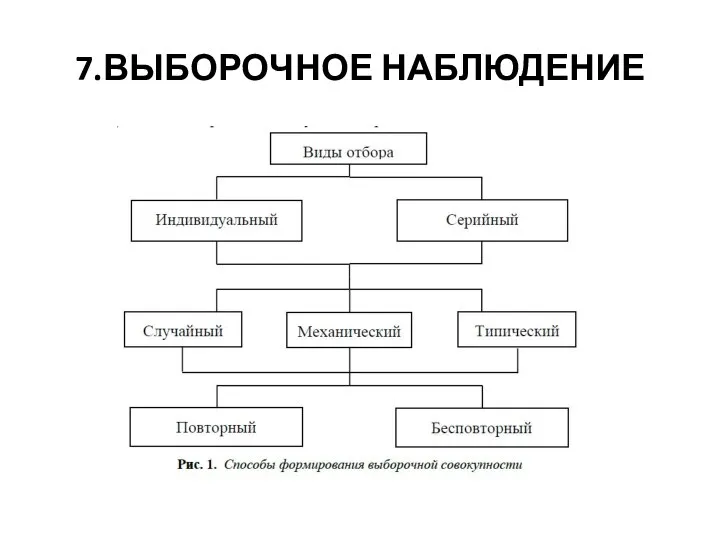
Слайд 267.ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Выборочное статистическое наблюдение- обследованию подвергается некоторая часть статистической совокупности, отобранная

особым образом, а результаты обследования распространяются на всю совокупность.
Полученные данные называются выборочной совокупностью или выборкой.
Слайд 287.ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Преимущества несплошного наблюдения :
требует меньших материальных и трудовых затрат;
позволяет

применять более совершенные способы учета;
повышает оперативное значение статистических данных, так как проводится в более короткие сроки.
Слайд 297.ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Средние генеральные - Х
- это пределы средней

величины какого-либо варьирующего признака, исчисляемой для всей генеральной совокупности.
~
Средние выборочные - Х
- это средняя величина этого же признака, исчисленная по выборочной совокупности.
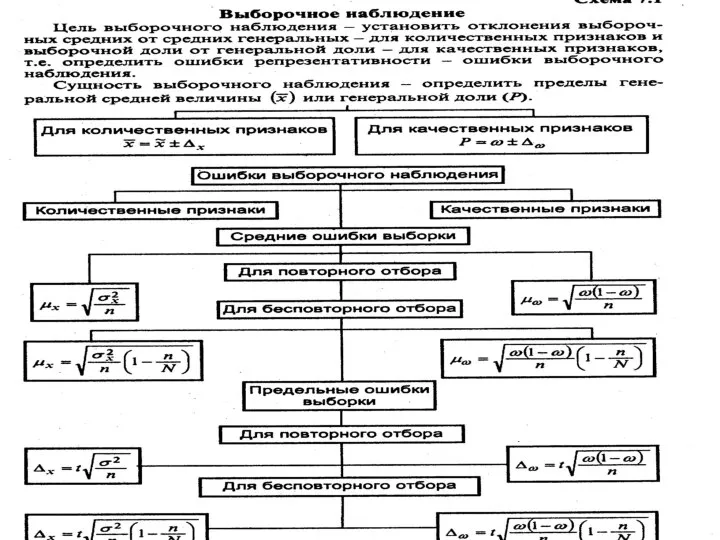
Слайд 307.ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Цель выборочного наблюдения – установить, с какой величиной

отклоняется значение выборочной средней от средней генеральной, т.е. какова ошибка выборочного наблюдения.
Слайд 317.1.Ошибки выборочного наблюдения
7.1.1. Средняя ошибка выборочной средней
Определяется по вариации количественного признака

(Х1, Х2, ... , Хn)
Слайд 32
7.1.2.Средняя ошибка выборочной доли
Определяется по показателям качественного или альтернативного признака.
m

ω = -------- - выборочная доля
n или частость,
где, n- число единиц всей выборочной совокупности ;
m - число единиц из этой совокупности, обладающих определенным признаком.
Слайд 337.1.2.Средняя ошибка выборочной доли
Для повторного отбора
Для бесповторного отбора
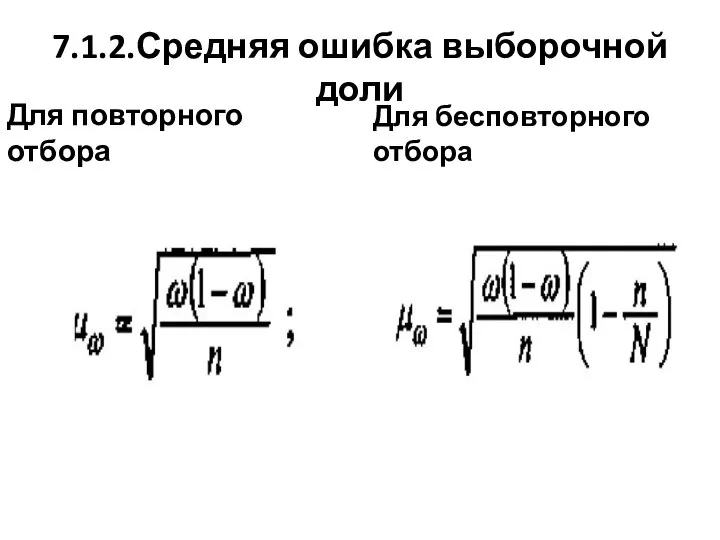
Слайд 347.1.3. Предельная ошибка выборки

Слайд 357.1.3. Предельная ошибка выборки

Слайд 36 7.1.4.Способы распространения выборочных данных на генеральную ……………………совокупность
Пределы генеральной средней величины

Х для количественного признака:
Слайд 37
7.1.4.Способы распространения выборочных данных на генеральную совокупность
Пределы генеральной доли качественного признака Р:

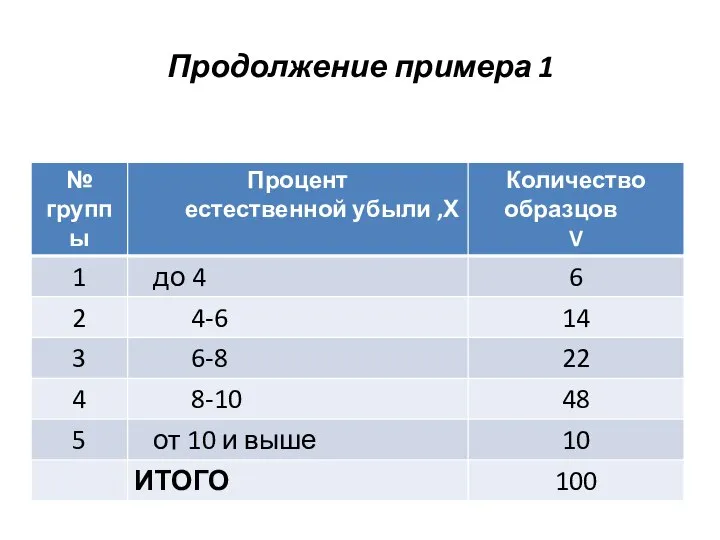
Слайд 40Продолжение примера 1
Для изучения естественной убыли произведено 5%-ное выборочное обследование партии

хранящихся на базе товаров. В результате лабораторного анализа установлено распределение образцов.
Слайд 41Продолжение примера 1
На основе показателей выборочной совокупности для всей партии товара,

т.е. генеральной совокупности, определите:
1) с вероятностью 0,954 возможные пределы доли продукции с естественной убылью от 10% и выше, т.е. размер нестандартной продукции;
2) с вероятностью 0,997 возможные пределы среднего процента естественной убыли.
Для определения средней ошибки выборочной средней по данным ряда распределения были исчислены средний процент естественной убыли в выборке и средний квадрат отклонения или дисперсия признака
Слайд 42Решение
Задание 1.
Дано из условия:
т=10 образцов - численность нестандартной

продукции;
n=100 образцов - численность выборочной совокупности;
N=2000 образцов - численность генеральной совокупности;
t=2 - коэффициент доверия, соответствующий вероятности 0,954_______________________________
Δ ω=?
Слайд 43Решение
Задание 1. Генеральная доля равна выборочной доле плюс-минус предельная ошибка выборки.
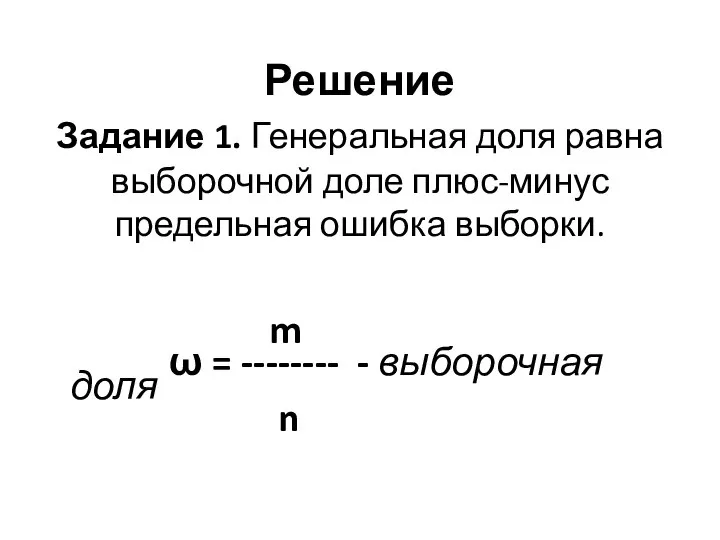
m
ω = -------- - выборочная доля
n
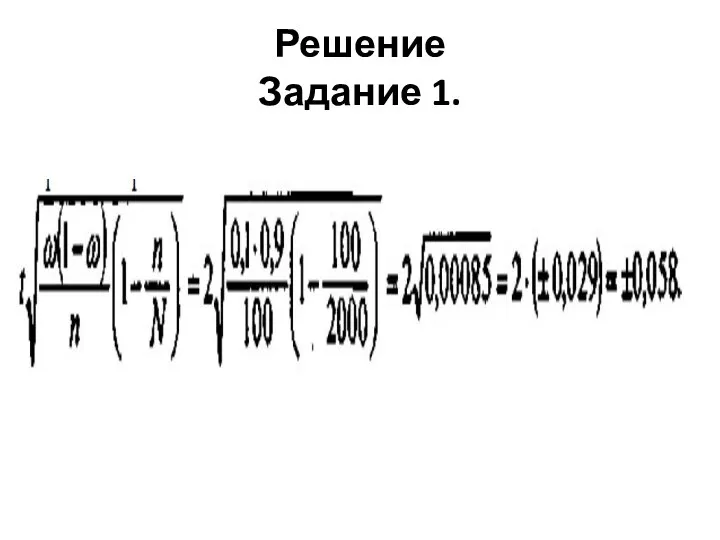
Слайд 46 Решение .Задание 1.
Выводы.
P = ω±Δω = 0,1 ± 0,058
Или в %:

10% ± 5,8%
Вывод: с вероятностью 0,954 продукция с естественной убылью от 10% и выше, т.е. нестандартная, в генеральной совокупности будет составлять от 4,2 до 15,8%.
Слайд 47Продолжение примера 1
На основе показателей выборочной совокупности для всей партии товара,

т.е. генеральной совокупности, определите:
2) с вероятностью 0,997 возможные преде-лы среднего процента естественной убыли.
Слайд 48
Решение
Задание 2.
Дано из условия:
n= 100 образцов - численность

выборочной совокупности;
N=2000 образцов - численность генеральной совокупности;
~
X = 7,84% - средний процент естественной убыли в выборочной совокупности;
σ² =4,36% - дисперсия процента естественной убыли в выборочной совокупности;
t=3 - коэффициент доверия, соответствующий вероятности 0,997________________________________
Δx =?
Слайд 49
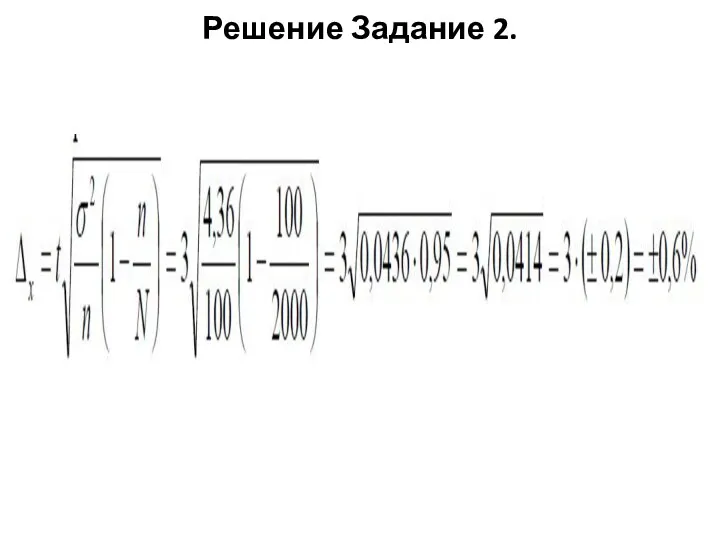
Решение Задание 2.
Полученные значения σ² и n, N подставим в формулу

предельной ошибки выборки для количественных признаков
Слайд 51 Задание 2.Выводы.
Х = 7,84 % ± 0,6 %
Вывод:

с вероятностью 0,997 можно утверждать что средний процент естественной убыли в генеральной совокупности будет заключаться в пределах от 7,24 до 8,44%.
![Рекомендуемая литература: 1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1022031/slide-1.jpg)







![6.1.2. Среднее линейное отклонение Для ранжированного ряда: ∑ [ Хi - Х]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1022031/slide-10.jpg)

































 Процент. Сорауларга җавап бирегез
Процент. Сорауларга җавап бирегез Масса. Весы
Масса. Весы Колесо истории математики
Колесо истории математики Одиниці вимірювання часу
Одиниці вимірювання часу Третий признак равенства треугольников. 7 класс
Третий признак равенства треугольников. 7 класс Предел функции в точке
Предел функции в точке Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Понятие производной
Понятие производной Математический тренажер
Математический тренажер Полином Жегалкина
Полином Жегалкина Презентация на тему Производная
Презентация на тему Производная  Возведение в степень произведения. 7 класс
Возведение в степень произведения. 7 класс Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Устный счёт. Назови числа по порядку
Устный счёт. Назови числа по порядку Признаки равенства треугольников
Признаки равенства треугольников Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период
Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период Готовимся к ЕГЭ
Готовимся к ЕГЭ Устный счет
Устный счет Арифметическая прогрессия
Арифметическая прогрессия Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Теория Графов
Теория Графов Взаимное расположение прямой и окружност
Взаимное расположение прямой и окружност Линейная алгебра
Линейная алгебра Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Координатный луч
Координатный луч Целое уравнение и его корни
Целое уравнение и его корни