Содержание
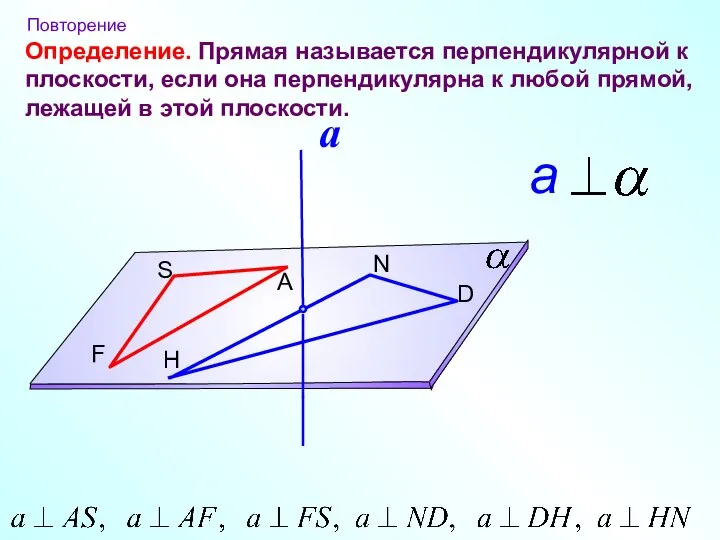
- 2. Определение. S A F N D H Прямая называется перпендикулярной к плоскости, если она перпендикулярна к
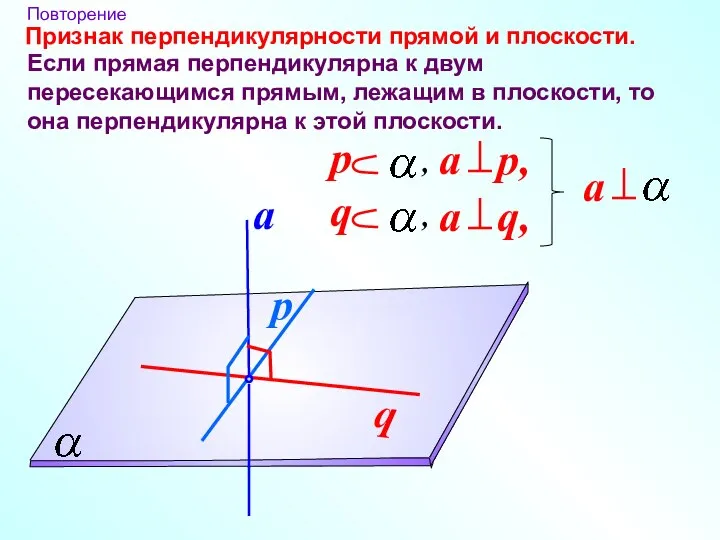
- 3. Признак перпендикулярности прямой и плоскости. Повторение Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости,
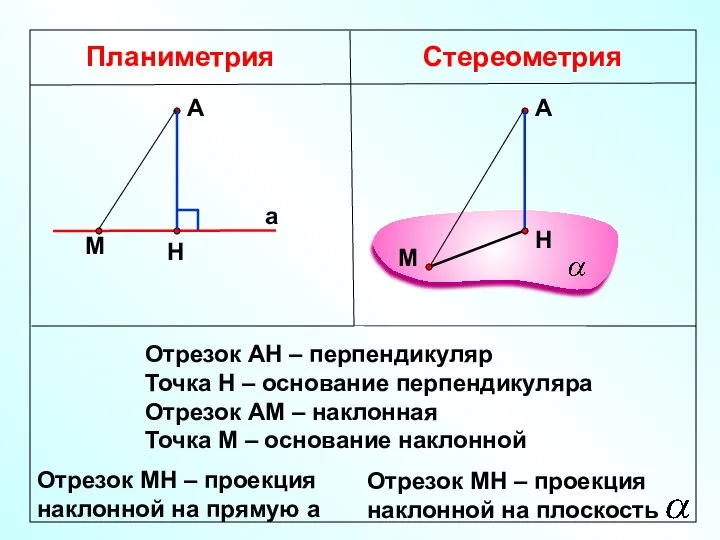
- 4. Планиметрия Стереометрия Отрезок АН – перпендикуляр Точка Н – основание перпендикуляра Отрезок АМ – наклонная Точка
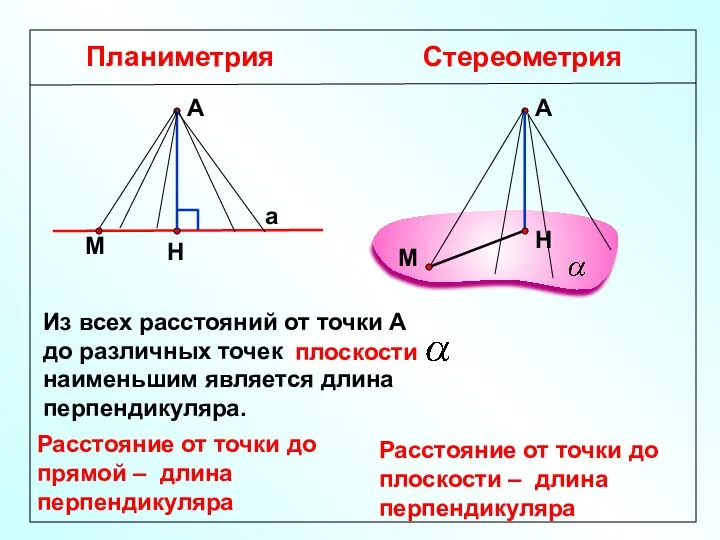
- 5. Планиметрия Стереометрия Расстояние от точки до прямой – длина перпендикуляра А а А Расстояние от точки
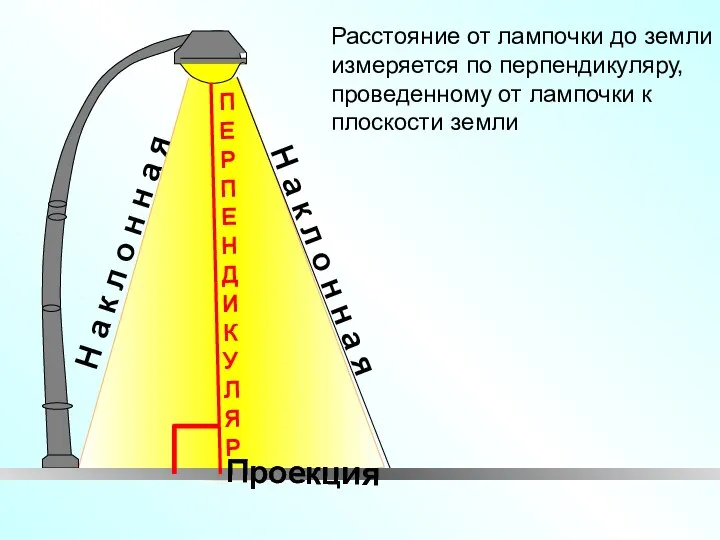
- 6. Расстояние от лампочки до земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли Н а
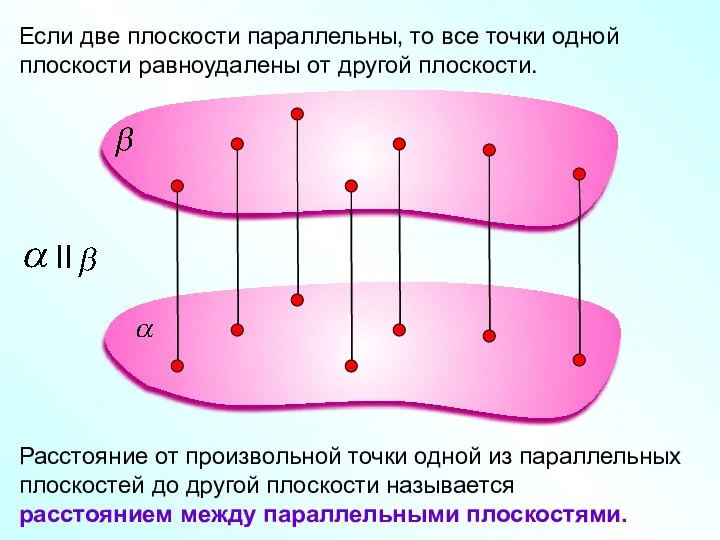
- 7. Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Расстояние от произвольной
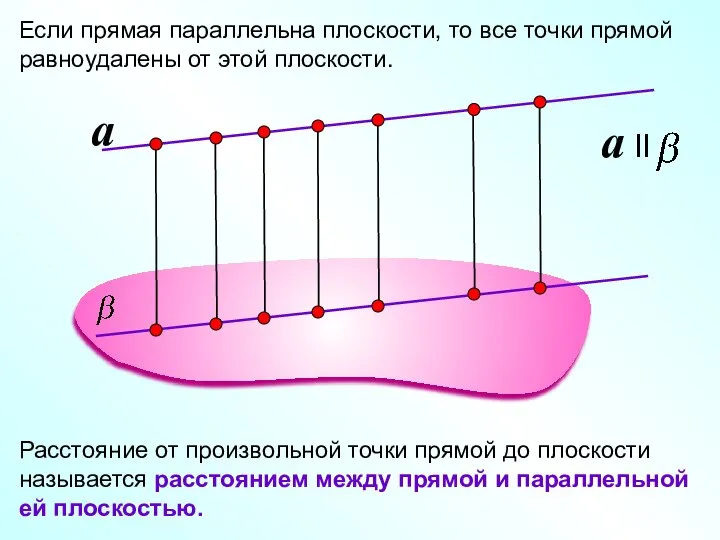
- 8. Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. a Расстояние от произвольной
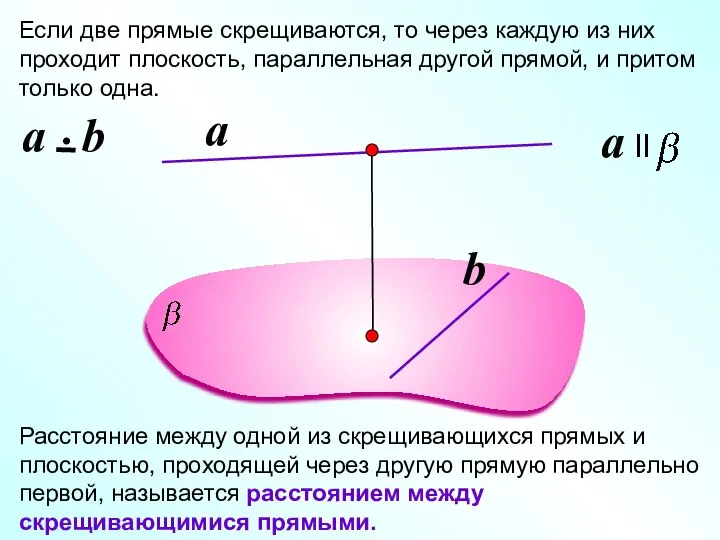
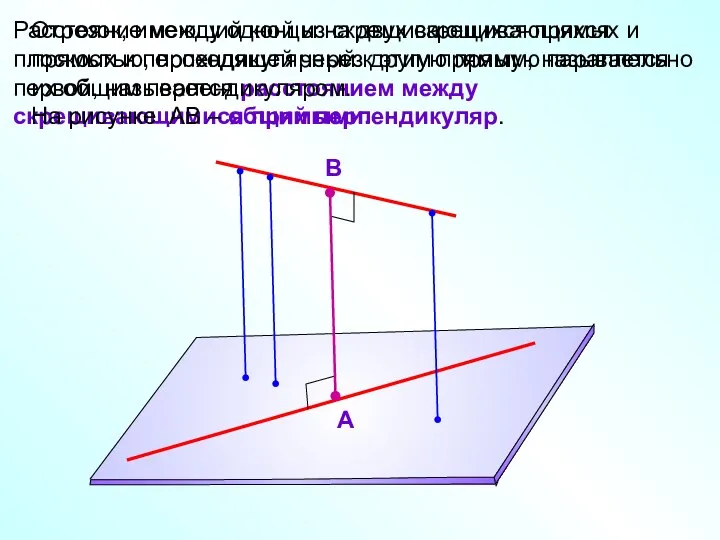
- 9. Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом
- 10. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием
- 11. В
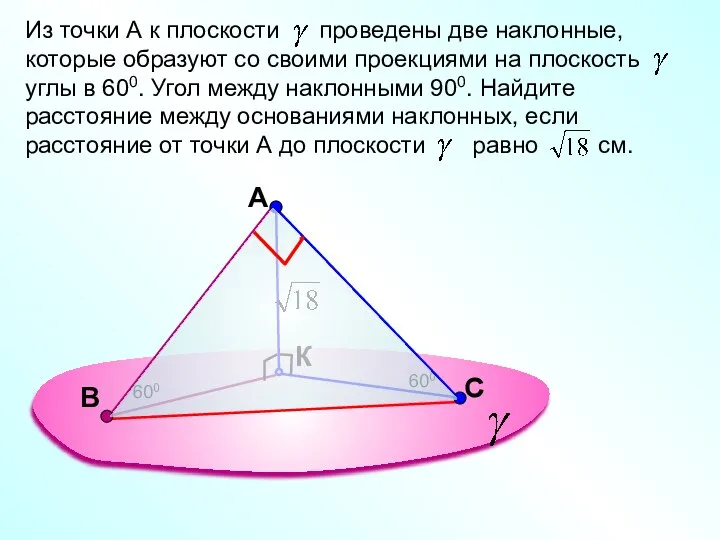
- 12. A К Из точки А к плоскости проведены две наклонные, которые образуют со своими проекциями на
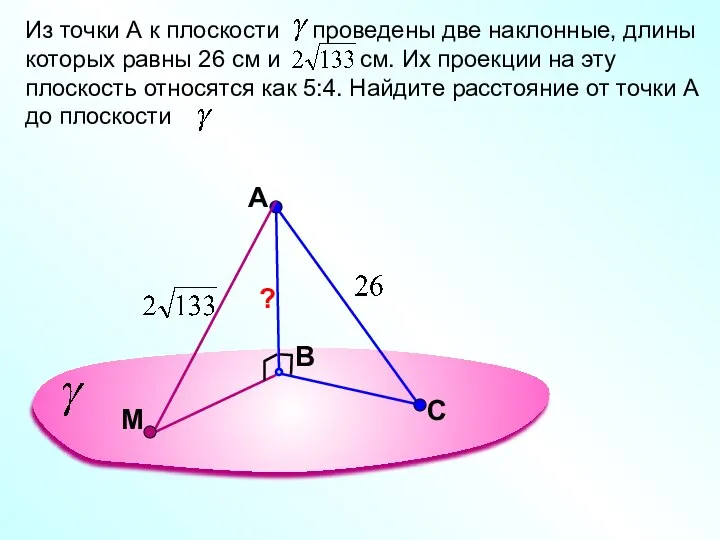
- 13. A В Из точки А к плоскости проведены две наклонные, длины которых равны 26 см и
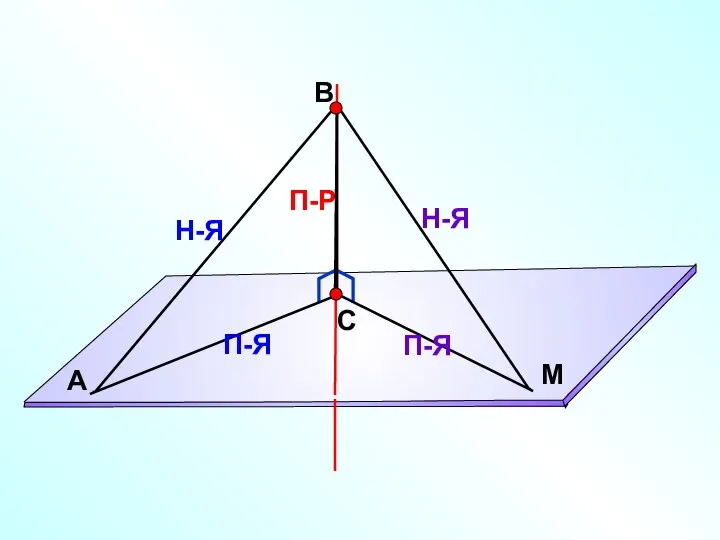
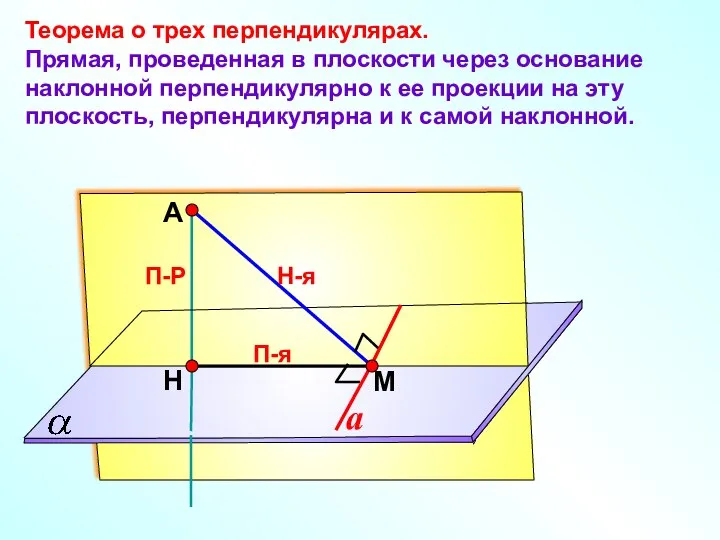
- 14. А Н П-Р М Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно
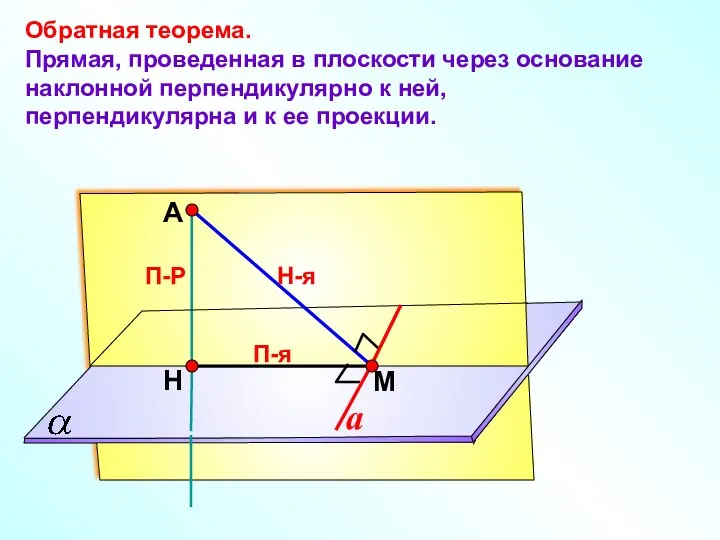
- 15. А Н П-Р М Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
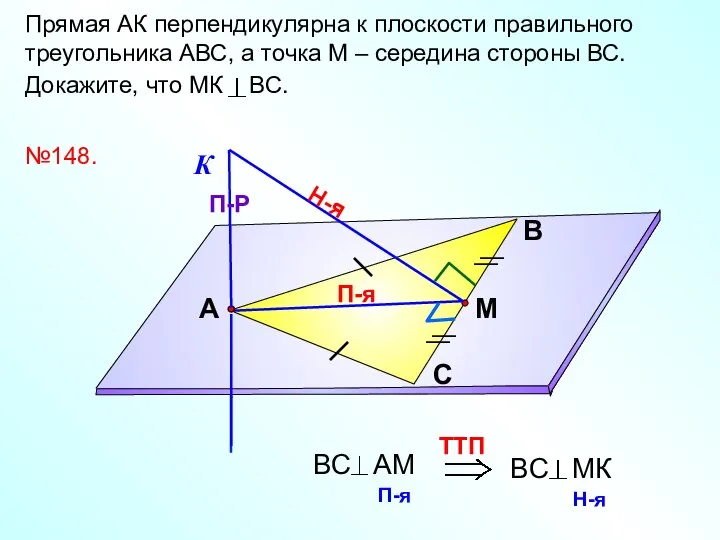
- 16. Прямая АК перпендикулярна к плоскости правильного треугольника АВС, а точка М – середина стороны ВС. Докажите,
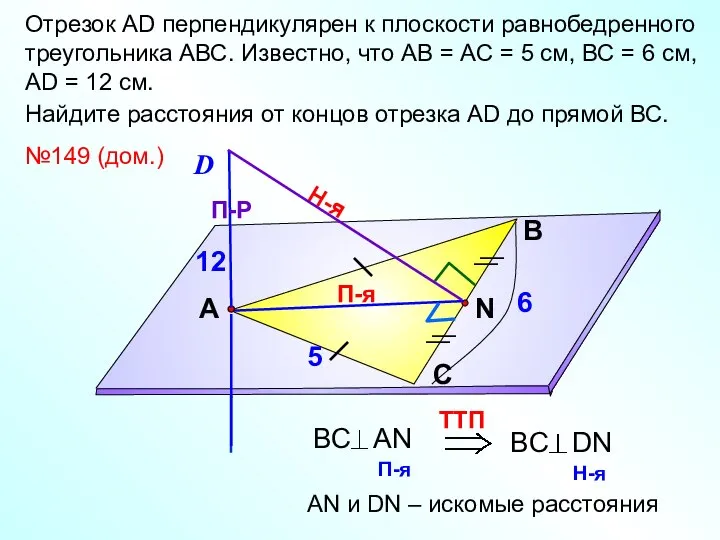
- 17. Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ = АС = 5 см,
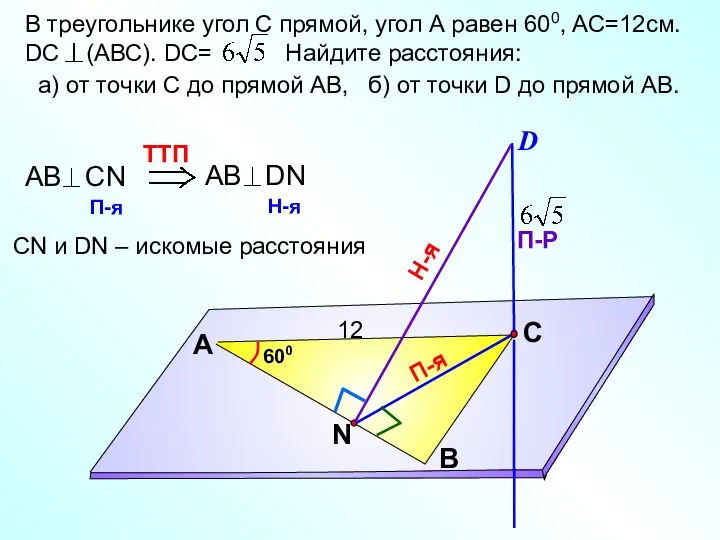
- 18. В треугольнике угол С прямой, угол А равен 600, AС=12см. DC (АВС). DC= Найдите расстояния: а)
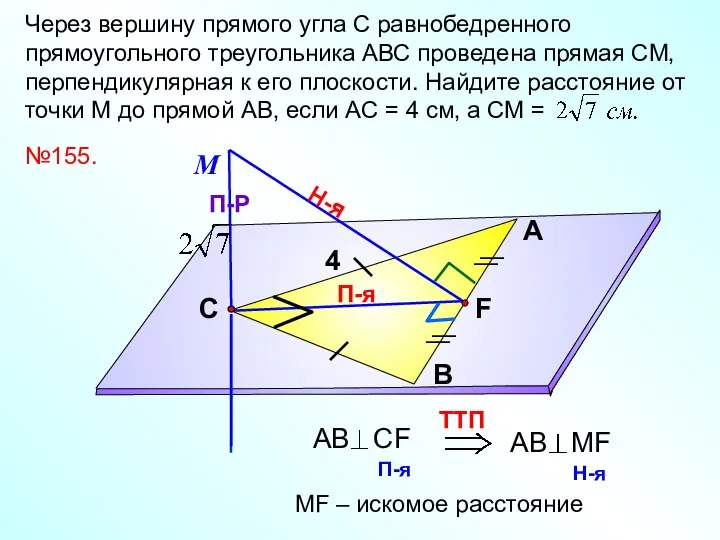
- 19. П-я Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена прямая СМ, перпендикулярная к его
- 21. Скачать презентацию
 Статистическая обработка вариационного ряда
Статистическая обработка вариационного ряда Преобразование иррациональных выражений
Преобразование иррациональных выражений Инструментальные средства работы с графической информацией. Лекция 3
Инструментальные средства работы с графической информацией. Лекция 3 Параллелограмм. Признаки параллелограмма
Параллелограмм. Признаки параллелограмма Багдадская математическая школа
Багдадская математическая школа Примеры на состав числа 6
Примеры на состав числа 6 Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Сложение и вычитание чисел в концентре 100 (1 класс Рудницкая В.Н. Школа XXI века)
Сложение и вычитание чисел в концентре 100 (1 класс Рудницкая В.Н. Школа XXI века) Відео. Задача на 2 дії
Відео. Задача на 2 дії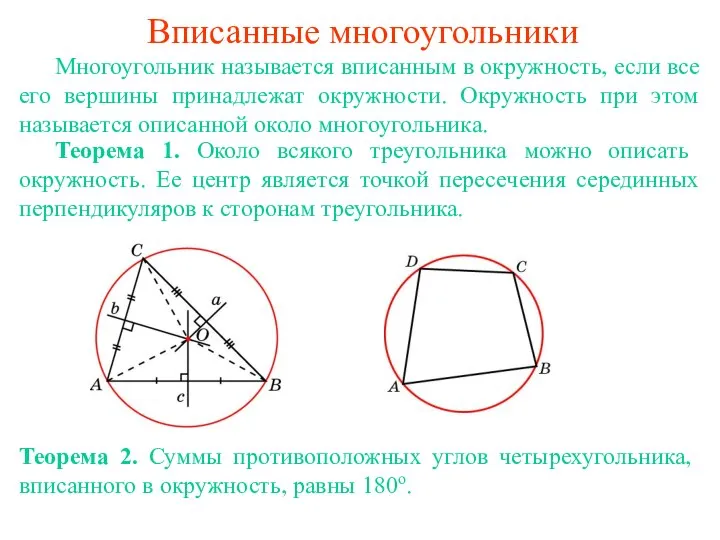 Вписанные и описанные многоугольники
Вписанные и описанные многоугольники Презентация на тему Скорость сближения и удаления
Презентация на тему Скорость сближения и удаления  Переместительное свойство умножения
Переместительное свойство умножения Preobrazovanie_grafikov_chislovykh_funktsiy
Preobrazovanie_grafikov_chislovykh_funktsiy Поліноми. Додавання поліномів
Поліноми. Додавання поліномів Площадь круга
Площадь круга Образование чисел, которые больше 20
Образование чисел, которые больше 20 Случаи сложения вида +7
Случаи сложения вида +7 Выборочное наблюдение. Статистическое наблюдение
Выборочное наблюдение. Статистическое наблюдение Повторение. Параллельные прямые
Повторение. Параллельные прямые Площадь параллелограмма
Площадь параллелограмма Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Операционный метод решения линейных дифференциальных уравнений и систем
Операционный метод решения линейных дифференциальных уравнений и систем Координаты вектора
Координаты вектора Задачи на движение. Рабочая тетрадь
Задачи на движение. Рабочая тетрадь Pirveladi statistikuri monacemebis damusavebis metodologia
Pirveladi statistikuri monacemebis damusavebis metodologia Векторный анализ и уравнения Максвелла
Векторный анализ и уравнения Максвелла Задачи на части
Задачи на части Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр
Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр