Область определения и область значений функции

Независимая переменная х — аргумент функции,
у — значение функции f в точке х, обозначают f(х).

Область определения функции у = f(х) —
множество значений х для которых существуют значения у и обозначают D(f).

Область значений функции —
множество, состоящее из всех чисел f(х), таких,
что х ∊ Х и обозначают Е(f).

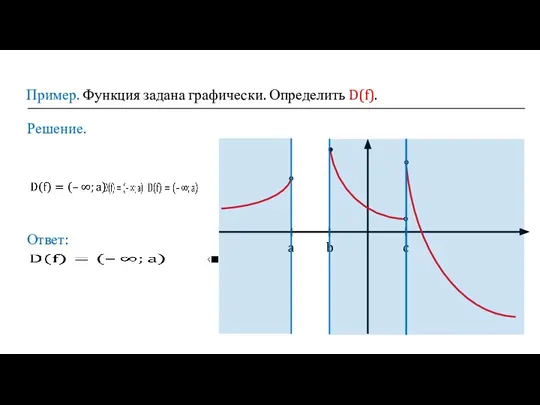
Пример. Функция задана графически. Определить D(f).
Решение.
a
b
c
Ответ:

Значения аргумента, которые обращают знаменатель в ноль – не входят в область определения данной функции.
Область определения рациональной функции

Решение.

Решение.

Область определения иррациональной функции

Решение.

Область определения функций с натуральным логарифмом
т.к. ln 1 = 0.

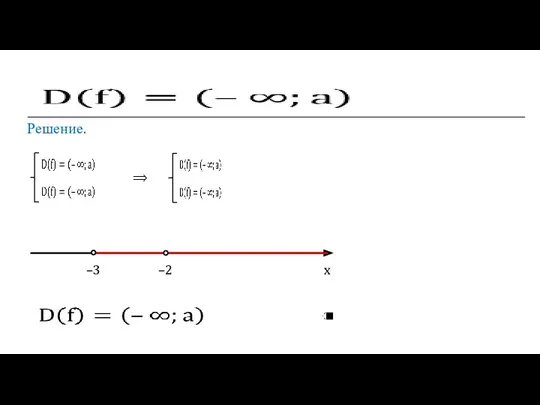
Решение.
⟹
–3
–2
x

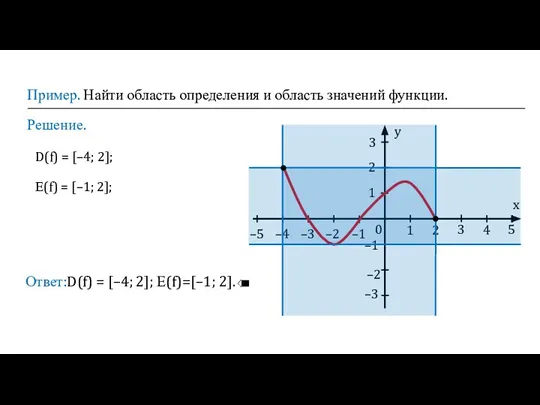
Пример. Найти область определения и область значений функции.
Решение.
Ответ:D(f) = [–4; 2]; Е(f)=[–1; 2].
x
y
0
1
2
3
4
5
–5
–4
–3
–2
–1
1
2
3
–3
–2
–1
D(f) = [–4; 2];
Е(f) = [–1; 2];

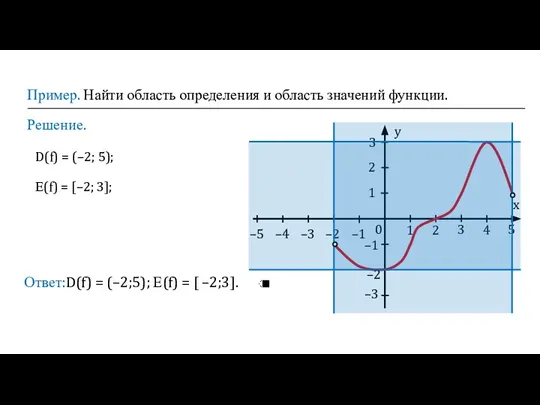
Пример. Найти область определения и область значений функции.
Решение.
Ответ:D(f) = (–2;5); Е(f) = [ –2;3].
x
y
0
1
2
3
4
5
–5
–4
–3
–2
–1
1
2
3
–3
–2
–1
D(f) = (–2; 5);
Е(f) = [–2; 3];