Содержание
- 2. Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля и каждый член, начиная
- 3. Назвать первый член и знаменатель геометрической прогрессии: 4, 2, 1, … -10, 20, -40, … -50,
- 4. Формула n-го члена геометрической прогрессии
- 5. Доказать, что последовательность, заданная формулой является геометрической прогрессией.
- 6. -геометрическая прогрессия, если для всех натуральных n выполняется равенство -знаменатель геометрической прогрессии (число) где
- 7. Доказать, что последовательность, заданная формулой является геометрической прогрессией. Решение: при всех n. -частное не зависит от
- 9. Скачать презентацию


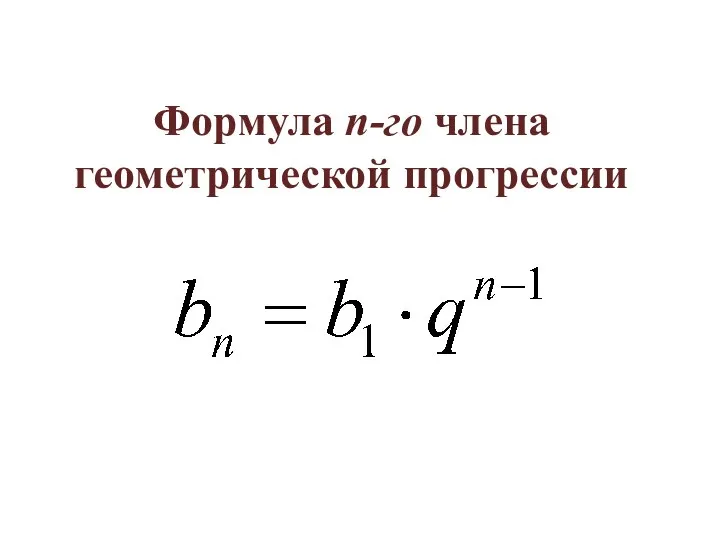



 Векторы. Решение задач
Векторы. Решение задач Алгебраические структуры
Алгебраические структуры Треугольник. Виды треугольников
Треугольник. Виды треугольников Векторы в пространстве
Векторы в пространстве Теорема Пифагора
Теорема Пифагора Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Конкретный смысл действия деления
Конкретный смысл действия деления Задача Печка
Задача Печка Волшебная страна - Геометрия
Волшебная страна - Геометрия Решение линейных уравнений. Часть 2
Решение линейных уравнений. Часть 2 Неопределенный интеграл. Лекция 2.1
Неопределенный интеграл. Лекция 2.1 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Математика. Лекция 1
Математика. Лекция 1 Решение неравенств
Решение неравенств Прямая Эйлера
Прямая Эйлера Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Тригонометрические уравнения и методы их решений
Тригонометрические уравнения и методы их решений Решение треугольников
Решение треугольников Алгебраические неравенства
Алгебраические неравенства Уравнение касательной к графику функции
Уравнение касательной к графику функции Формулы дифференцирования
Формулы дифференцирования Признаки равенства треугольников
Признаки равенства треугольников Задача на тему Прогрессия
Задача на тему Прогрессия Круг. Шар. Сфера
Круг. Шар. Сфера Свойства касательных к окружности. 7 класс
Свойства касательных к окружности. 7 класс Пропорции. Задачи
Пропорции. Задачи Десятичный и натуральный логарифм
Десятичный и натуральный логарифм