Пирамида и её элементы. Правильная пирамида

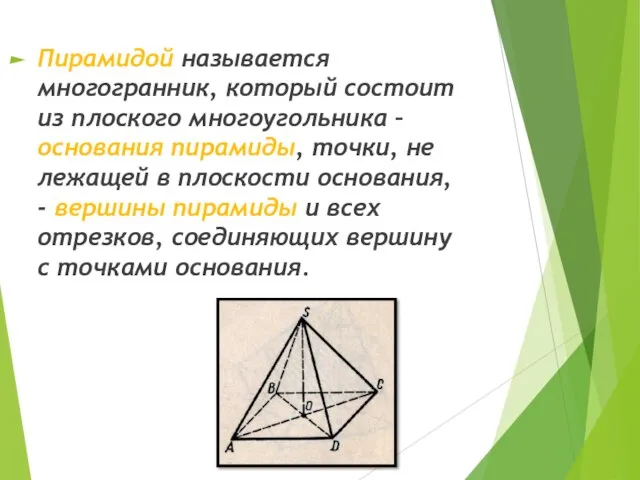
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину с точками основания.

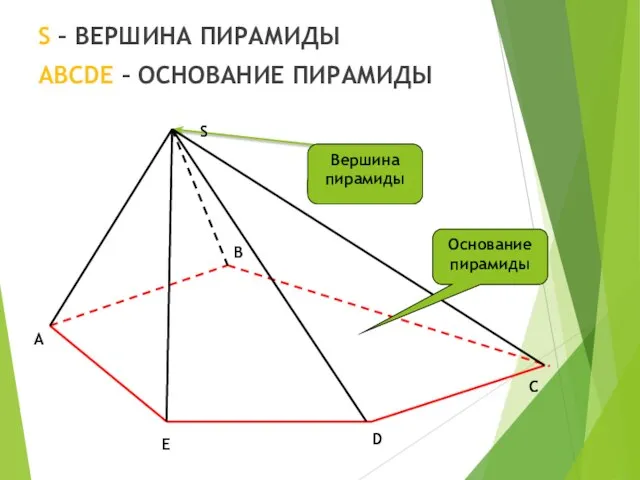
S – ВЕРШИНА ПИРАМИДЫ
ABCDE – ОСНОВАНИЕ ПИРАМИДЫ
C
Основание пирамиды
Вершина пирамиды

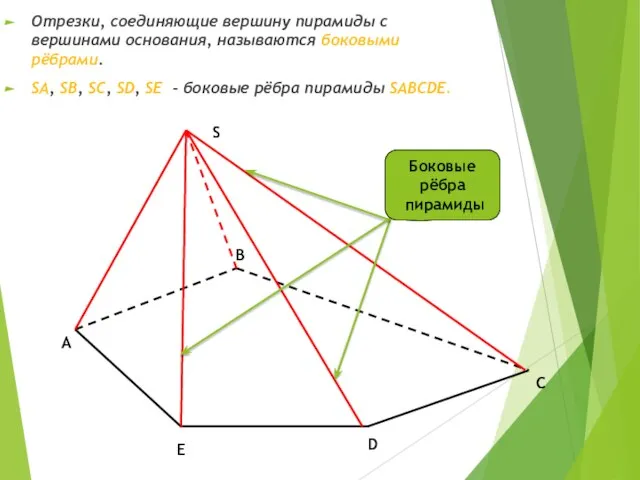
C
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами.
SA, SB, SC, SD, SE - боковые рёбра пирамиды SABCDЕ.
Боковые рёбра
пирамиды

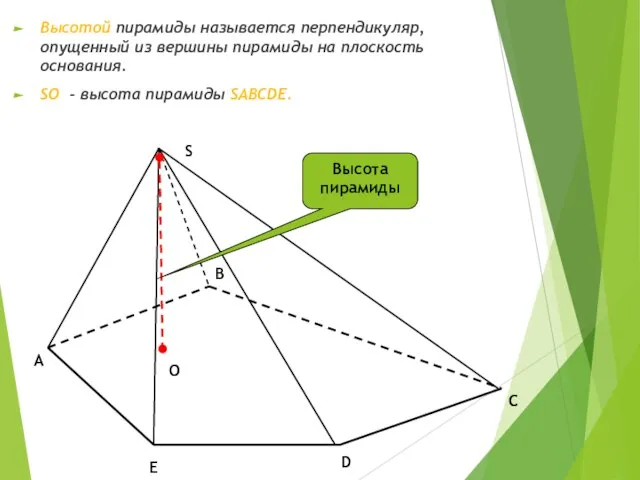
C
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
SО - высота пирамиды SABCDЕ.
О
Высота пирамиды

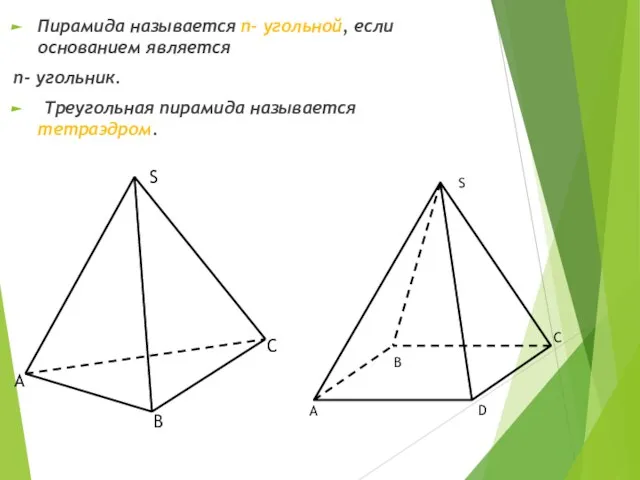
Пирамида называется n- угольной, если основанием является
n- угольник.
Треугольная пирамида называется тетраэдром.
C

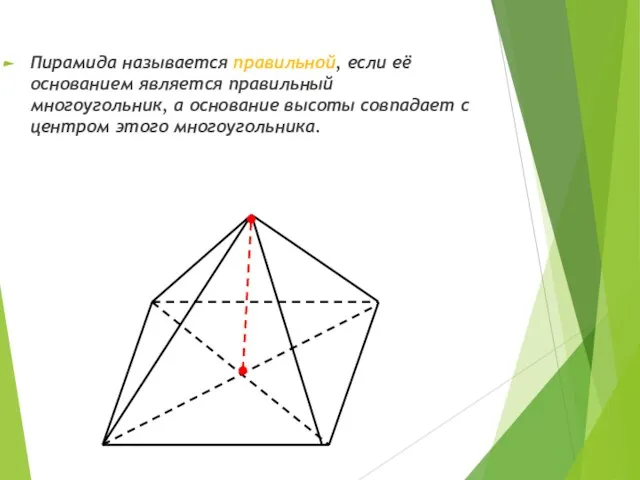
Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.

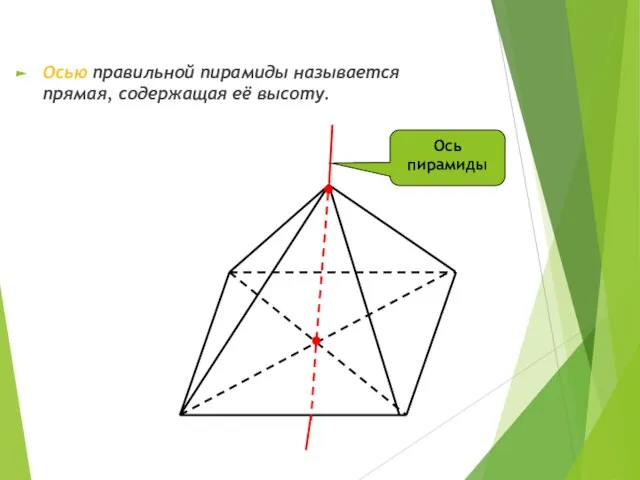
Осью правильной пирамиды называется прямая, содержащая её высоту.
Ось пирамиды

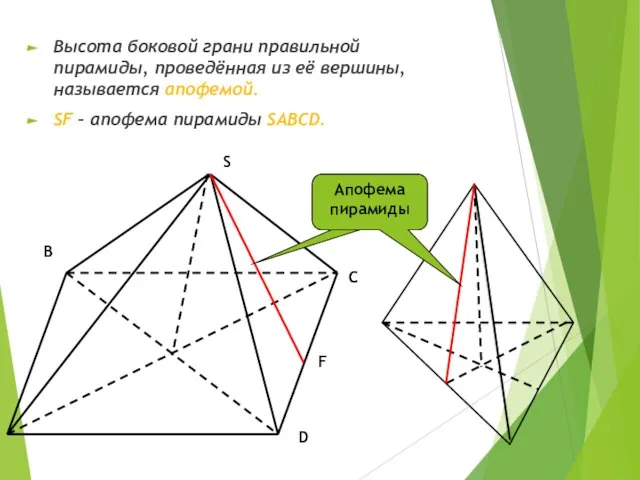
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
SF – апофема пирамиды SABCD.
Апофема пирамиды
Апофема пирамиды

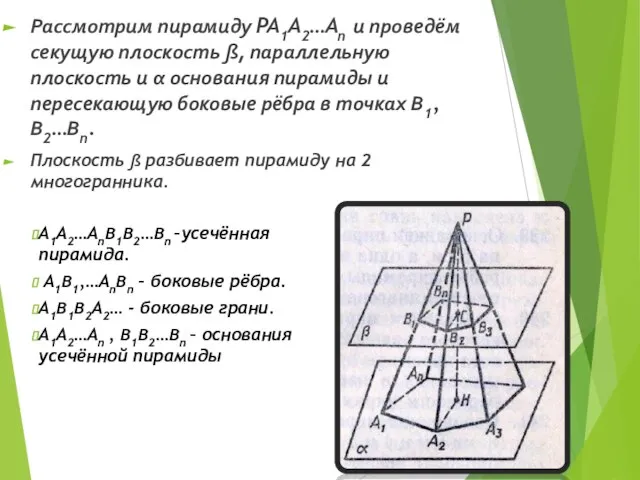
Усечённая пирамида

Рассмотрим пирамиду PA1A2…An и проведём секущую плоскость ß, параллельную плоскость и α основания пирамиды и пересекающую боковые рёбра в точках В1,В2…Вn.
Плоскость ß разбивает пирамиду на 2 многогранника.
A1A2…AnВ1В2…Вn –усечённая пирамида.
A1В1,…AnВn – боковые рёбра.
A1В1В2A2… - боковые грани.
A1A2…An , В1В2…Вn – основания усечённой пирамиды

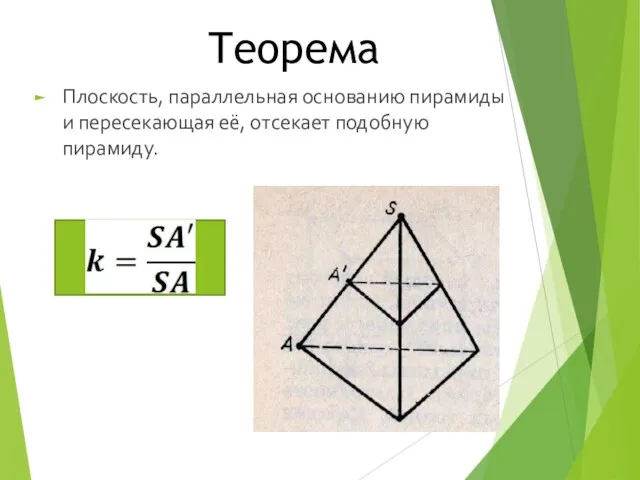
Теорема
Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду.

Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Площадь боковой поверхности пирамиды

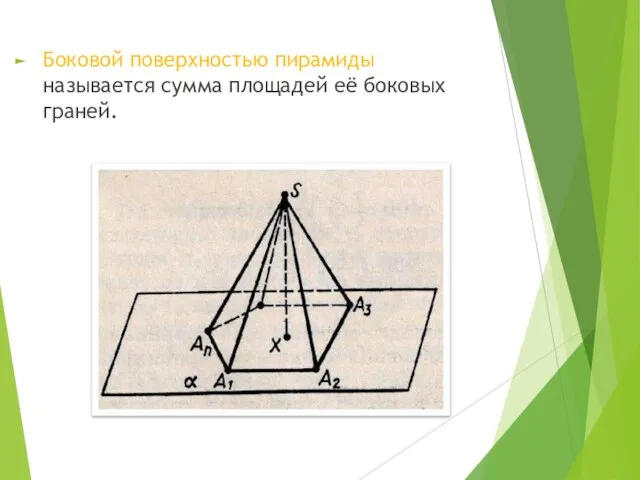
Боковой поверхностью пирамиды называется сумма площадей её боковых граней.

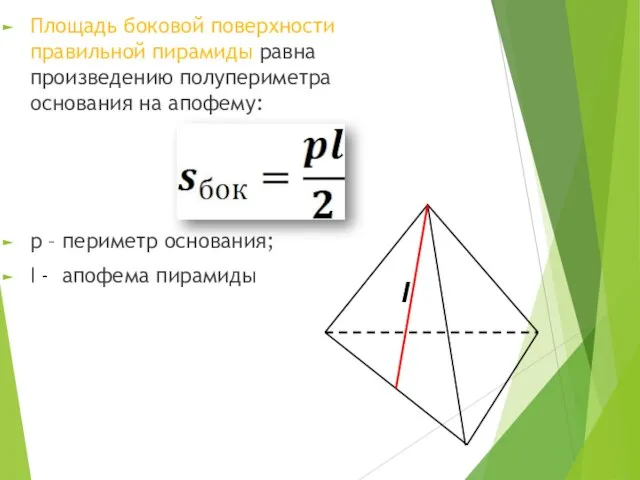
Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему:
p – периметр основания;
l - апофема пирамиды

Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему:
p1 и p2 – периметры оснований;
l - апофема пирамиды.

Площадь полной поверхности пирамиды

Площадь полной поверхности правильной пирамиды равна сумме площади боковой поверхности и площади основания:

Объём пирамиды

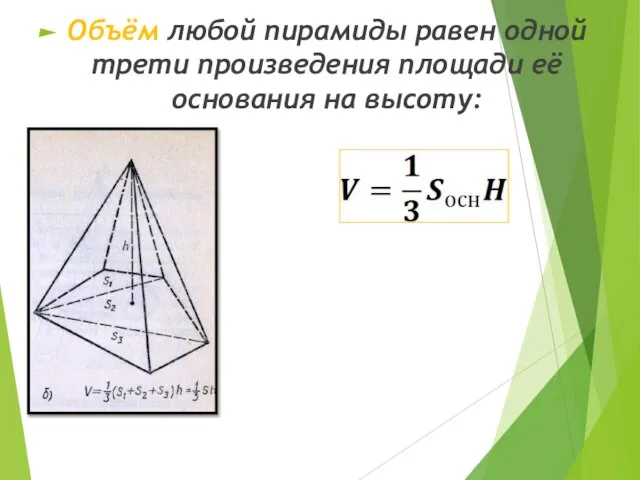
Объём любой пирамиды равен одной трети произведения площади её основания на высоту:

Объём усечённой пирамиды

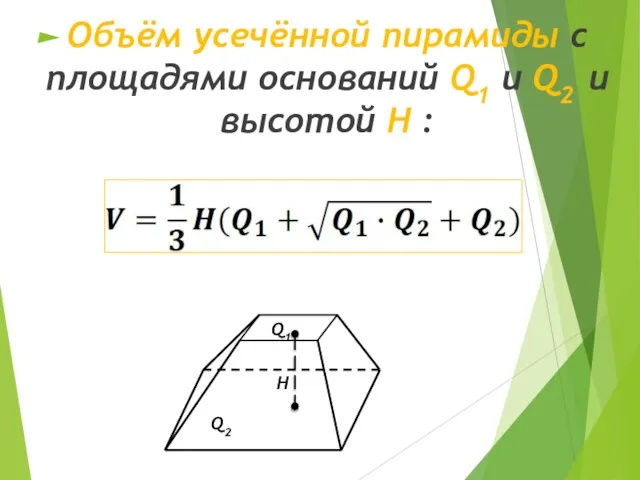
Объём усечённой пирамиды с площадями оснований Q1 и Q2 и высотой H :

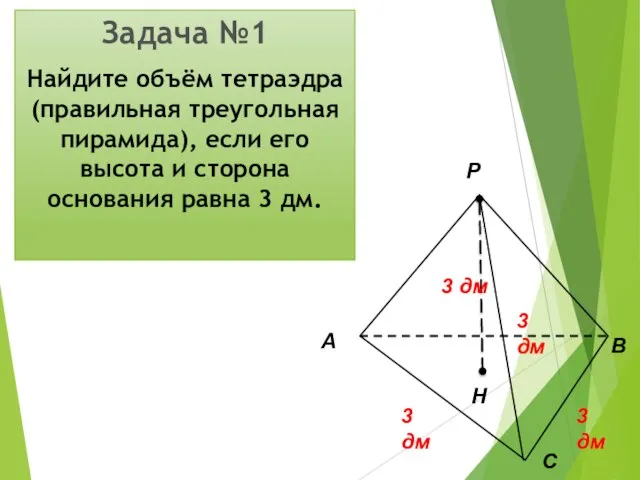
Задача №1
Найдите объём тетраэдра (правильная треугольная пирамида), если его высота и сторона основания равна 3 дм.