Содержание
- 2. Основы статистического моделирования Задача математического моделирования состоит в построении математической модели объекта и в количественной оценке
- 3. Статические модели описывают связь между входными и выходными параметрами объекта в стационарном состоянии. Стационарное состояние –
- 4. Основы статистического моделирования Динамические модели связывают вход и выход объекта в переходных состояниях. Переходное состояние –
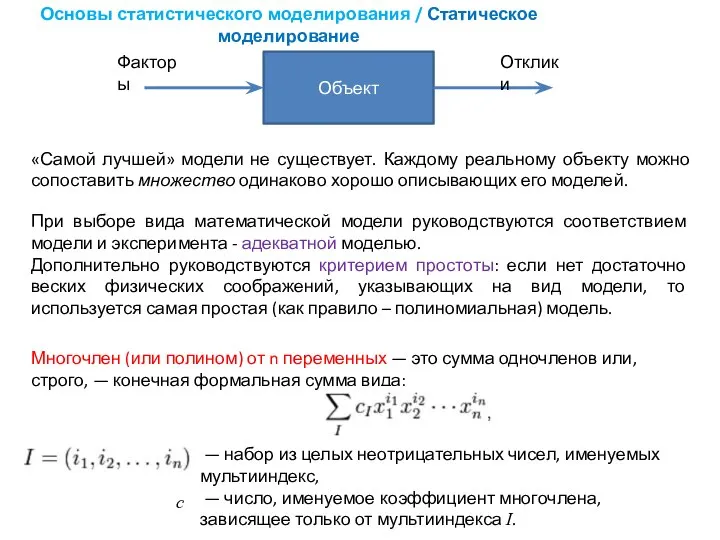
- 5. Основы статистического моделирования / Статическое моделирование Многочлен (или полином) от n переменных — это сумма одночленов
- 6. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Вероятностью события А в некотором процессе операции
- 7. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Теорема сложения вероятностей для произвольных событий Теорема
- 8. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ ∀ {A | Ai ∩ Aj =
- 9. События А и В называются независимыми (или, по-другому, взаимно-независимыми) Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ
- 10. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / УСЛОВНЫЕ ВЕРОЯТНОСТИ -
- 11. ФОРМУЛА БАЙЕСА Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / УСЛОВНЫЕ ВЕРОЯТНОСТИ - эта
- 12. ФОРМУЛА БАЙЕСА Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / УСЛОВНЫЕ ВЕРОЯТНОСТИ Полная группа
- 13. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Основой комбинаторики
- 14. Основные комбинаторные схемы Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ РАЗМЕЩЕНИЕ
- 15. Основные комбинаторные схемы Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ ПЕРЕСТАНОВКА
- 16. Основные комбинаторные схемы Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ КОМБИНАЦИЯ
- 17. Основные комбинаторные схемы Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ КОМБИНАЦИЯ
- 18. СХЕМА И ФОРМУЛА БЕРНУЛЛИ Основные комбинаторные схемы Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
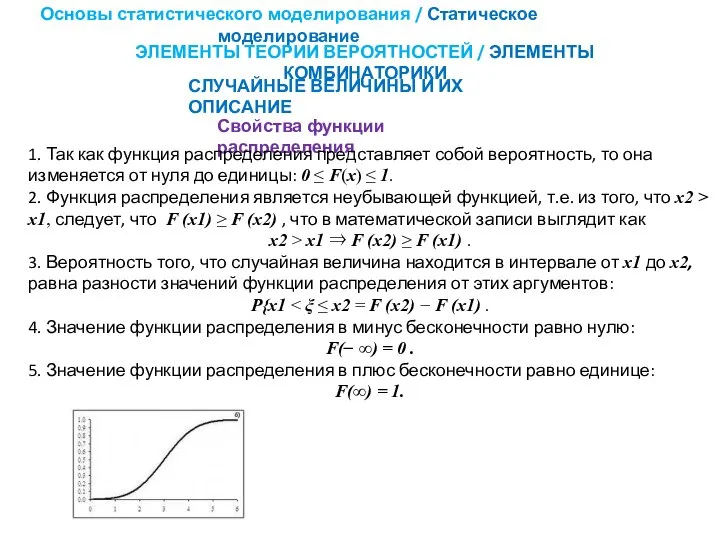
- 19. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ
- 20. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ
- 21. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ
- 22. Основы статистического моделирования / Статическое моделирование ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ / ЭЛЕМЕНТЫ КОМБИНАТОРИКИ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ
- 24. Скачать презентацию


















 Решите неравенства
Решите неравенства Числовые и буквенные выражения
Числовые и буквенные выражения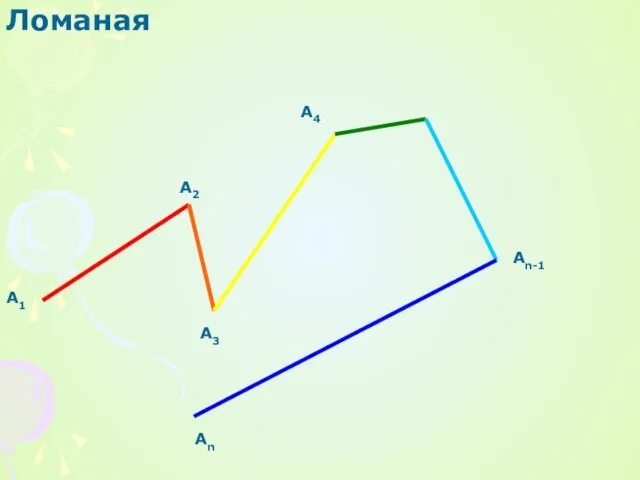 Презентация на тему Ломаная
Презентация на тему Ломаная  Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Математическая статистика
Математическая статистика Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Построение сечений
Построение сечений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА
Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА  Серединный перпендикуляр
Серединный перпендикуляр Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Сложение чисел
Сложение чисел Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Площадь трапеции
Площадь трапеции Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Величины. Свойства величин
Величины. Свойства величин Функции. ЕГЭ
Функции. ЕГЭ Многочлены. Задания
Многочлены. Задания Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Умножение. Законы умножения
Умножение. Законы умножения Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Пушкин и математика
Пушкин и математика