Слайд 4В данном курсе можно выделить три главные линии.
Во-первых, в курсе изучаются

так называемые основания математики (теория множеств и математическая логика).
Во-вторых– теоретические основы современной информатики(теория алгоритмов и вычислимых функций, теория кодирования, алгебра логики).
В третьих– те факты, методы и конструкции дискретной математики, которые применяются в экономико-математических моделях.
Слайд 12В общем случае, множество A по схеме свертывания определяется как множество, которое

содержит все элементы из K, обладающие свойством F.
A = {x| x обладает свойством F}.
Слайд 13Применяя сокращение F(x) для обозначения того, что элемент x обладает свойством F,

будем писать
A= {x| F(x)}.
Очевидно, что F(x)∈ {0,1}.
F(x) называется предикатом.
Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектом высказывания называется то, о чём делается утверждение.
Слайд 14Неограниченное применение схемы свертывания ведет к противоречиям. Например, можно получить «множество всех

множеств»:
M= {x| x– множество}.
Если считать M множеством, то получаем M∈M.
Рассмотрим парадокс Рассела, открытый в1902 году.
Слайд 15Назовем множество правильным, если оно не является своим элементом, и неправильным в

противном случае. Определим множество R как множество всех правильных множеств. Более формально:
R= {x| x∉R}.
Слайд 16В соответствии с определением для любого множества A справедливо утверждение:
A∈R тогда

и только тогда, когда A∉A.
В частности, если считать R множеством, то его само можно взять в качестве A, но тогда мы придем к противоречию:
R∈R тогда и только тогда, когда R∉R.
Слайд 17Более подробно. Если R правильное, то есть не является своим элементом, то

оно должно находиться в R, то есть быть своим элементом.
Если же R неправильное, то оно является своим элементом, то есть содержится в R, но R содержит только правильные множества.
Таким образом, R не может быть ни правильным, ни неправильным.
Слайд 46Для обозначения бинарного отношения R на множестве M, будем использовать как обозначение

(a,b)∈R,
так и обозначение
aRb,
где a∈M, b∈M
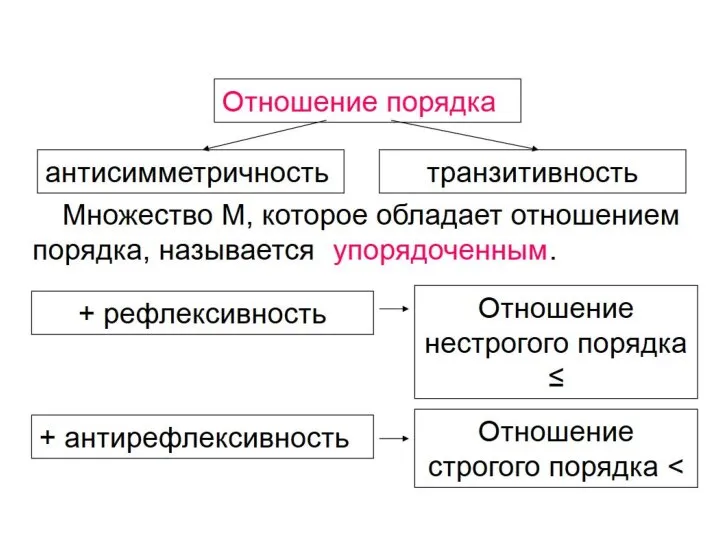
Слайд 71Отношение порядка.
Пусть А– непустое множество.
Определение. Отношение Р ⊆ А называется

предпорядком (квази-порядком), если оно рефлексивно и транзитивно.
Слайд 72Пример. Пусть А= {a, b, c, d}.
Отношение Р= {(a, a), (a,
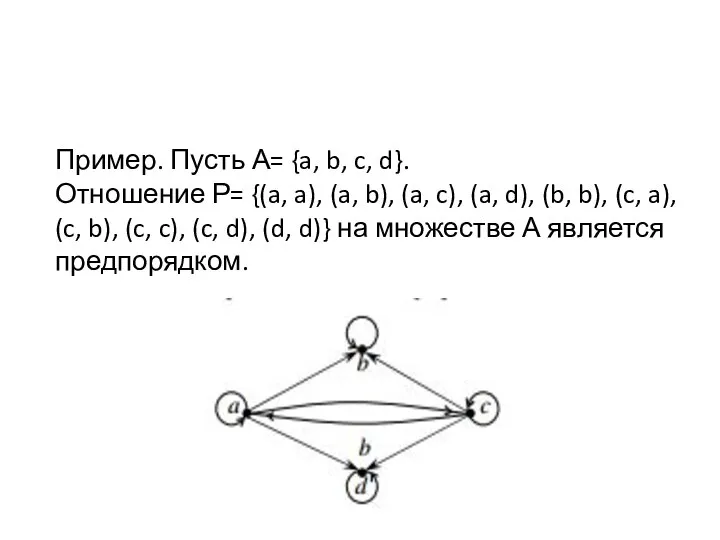
b), (a, c), (a, d), (b, b), (c, a), (c, b), (c, c), (c, d), (d, d)} на множестве А является предпорядком.
Слайд 73Определение. Отношение Р ⊆ А называется частичным порядком, если оно рефлексивно, транзитивно

и антисимметрично. Таким образом, частичный порядок представляет собой антисимметричный предпорядок. Частичный порядок обозначается символом ≤.
Слайд 74Определение. Отношение < ⊆ А называется строгим порядком, если оно определяется по

следующему правилу: (∀ x, y ∈ A) х < у ⇔ х ≤ у и х ≠ у.
Отношение строгого порядка не является частичным порядком, так как оно не рефлексивно.
Слайд 75Определение. Пусть ≤ ⊆ А и х, у ∈ А. Элементы х

и у называются несравнимыми, если нельзя сказать, что х ≤ у или у ≤ х.
Пример. Пусть А= {a, b, c, d}. Отношение включения ⊆ на булеане P(A) является частичным порядком. Элементы B= {a, c} и C= {b, d} из P(A)
являются несравнимыми, так как(B, C) ∉ ⊆ и(C, B) ∉ ⊆.
Слайд 76Определение. Частичный порядок ≤ ⊆ А называется линейным порядком, если(∀ х, у

∈ А) х ≤ у или у ≤ х.
Определение. Пусть А ≠ ∅ и ≤– частичный(линейный) порядок на А.
Упорядоченная пара <А,≤> называется частично(линейно) упорядоченным множеством.
Слайд 77Пример. Пара < Z, ≤>, где ≤– отношение делимости на множестве Z,

является частичным, но не линейным порядком.
Пары < N, ≤> , < R, ≤> с обычными отношениями ≤ образуют линейно упорядоченные множества.
Слайд 78Определение. Элемент а ∈ А частично упорядоченного множества < А, ≤ >

называется максимальным(минимальным), если(∀х∈А) а ≤ х(х ≤ а) ⇒ х = а.
Определение. Элемент а ∈ А частично упорядоченного множества < А, ≤ > называется наибольшим(наименьшим), если(∀ х ∈ А) х ≤ а(а ≤ х).
Слайд 79Наибольший(наименьший) элемент частично упорядоченного множества
< А, ≤ >(если он существует) обозначается через

max A (min А).
Слайд 80Теорема. Пусть < А, ≤ > является частично упорядоченным множеством, где А–

непустое и конечное множество. Тогда < А, ≤ > содержит хотя бы один минимальный элемент, и если он является единственным, то он также является и наименьшим. Аналогично, < А, ≤ > содержит хотя бы один максимальный элемент, и если он является единственным, то он также является наибольшим.
Слайд 81Пример. Частично упорядоченное множество < А, ≤ >, где
А= {a, b, c,
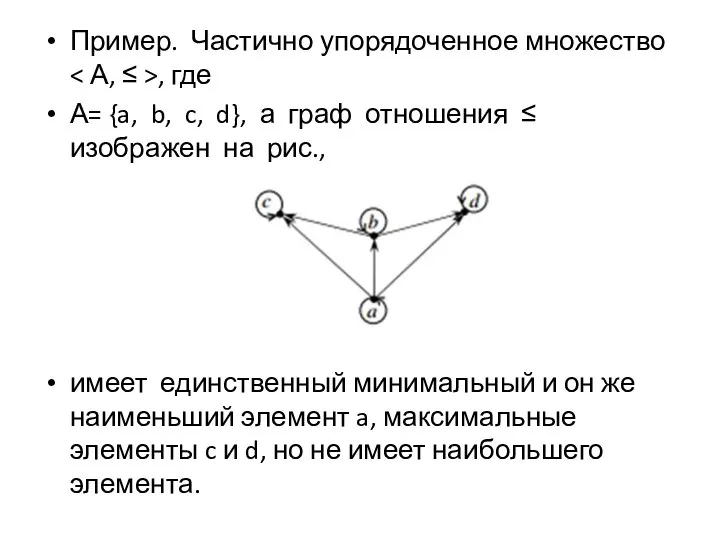
d}, а граф отношения ≤ изображен на рис.,
имеет единственный минимальный и он же наименьший элемент a, максимальные элементы c и d, но не имеет наибольшего элемента.
Слайд 82Пример3.22. Частично упорядоченное множество < B, ≤ >, где
B= {1, 2, 3,
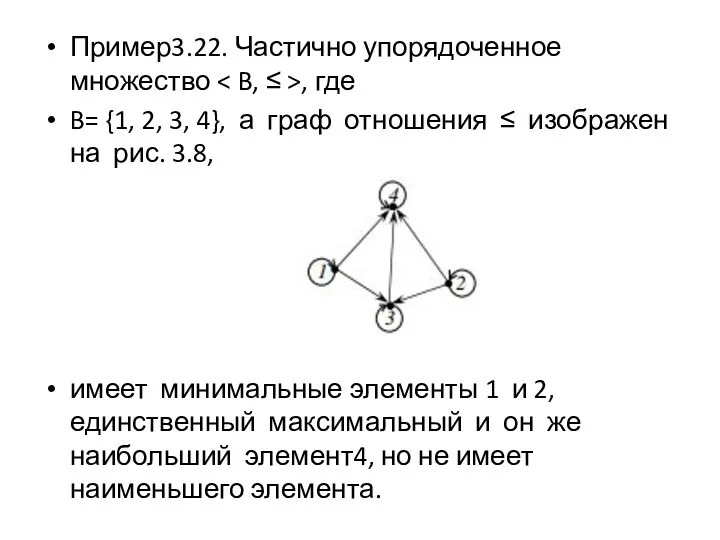
4}, а граф отношения ≤ изображен на рис. 3.8,
имеет минимальные элементы 1 и 2, единственный максимальный и он же наибольший элемент4, но не имеет наименьшего элемента.
Слайд 83Замечание. Всякий наибольший элемент частично упорядоченного множества является максимальным, а всякий наименьший

элемент – минимальным. Обратное утверждение, вообще говоря, неверно.
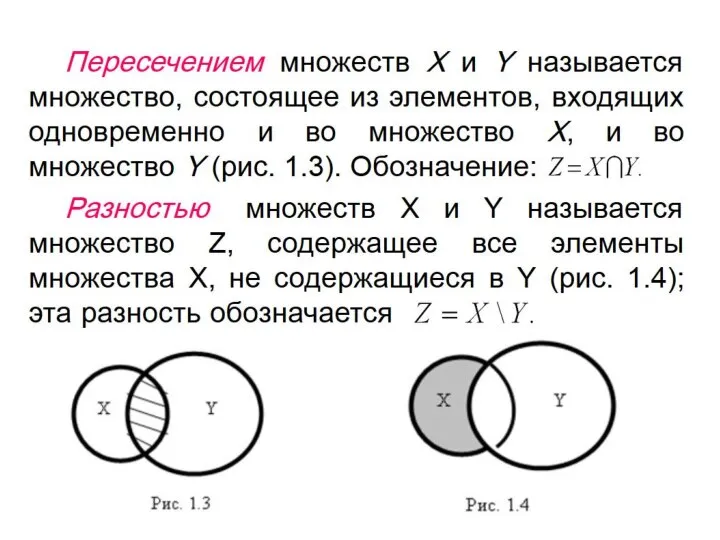
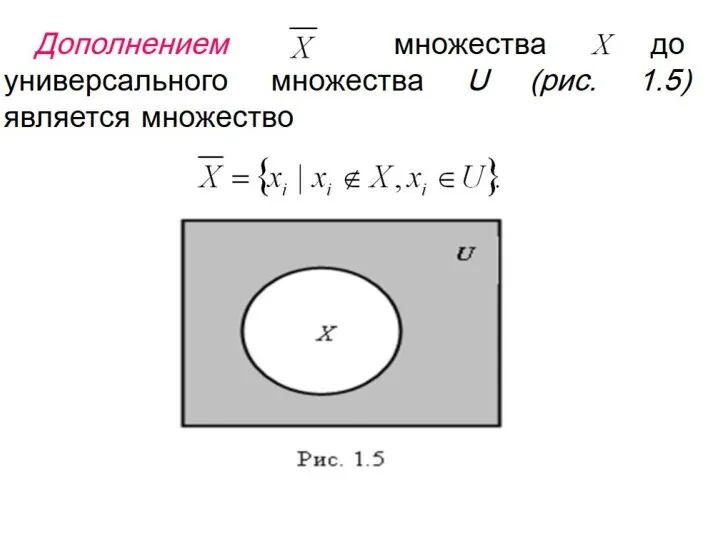
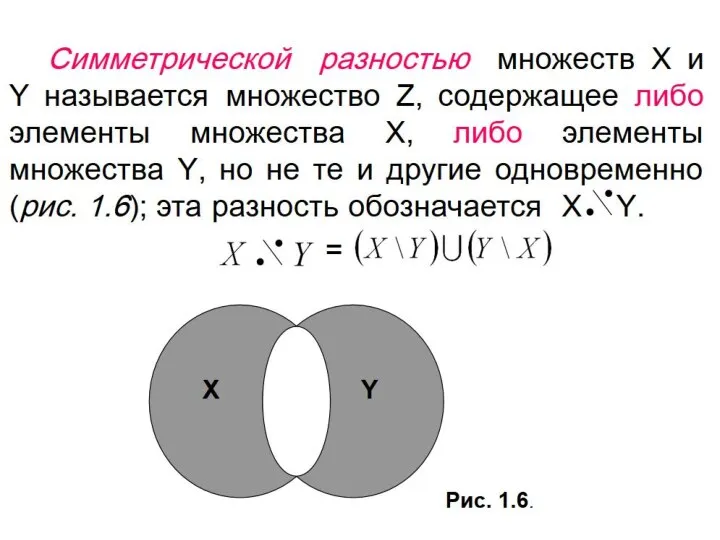
Слайд 87Операции над отношениями
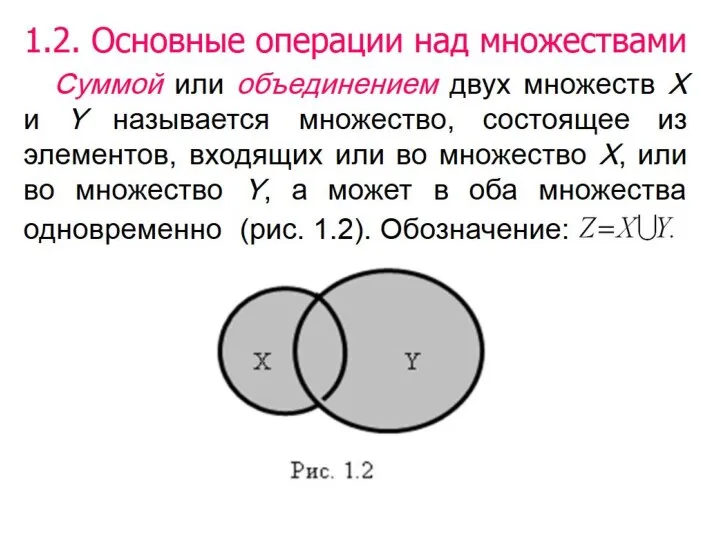
Так как отношения, заданные на фиксированной паре множеств являются подмножества

множества A×B, то можно определить операции объединения, пересечения и дополнения отношений.
Слайд 89Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции

и отрицании.


































































































 Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Прогрессии
Прогрессии Кривые второго порядка. Практика
Кривые второго порядка. Практика Эскизы кривых на плоскости, заданных параметрически
Эскизы кривых на плоскости, заданных параметрически Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Симметрия. Осевая и центральная симметрии
Презентация на тему Симметрия. Осевая и центральная симметрии  Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Математический КВН
Математический КВН Преобразование графиков
Преобразование графиков Величины. Масса (1 класс)
Величины. Масса (1 класс)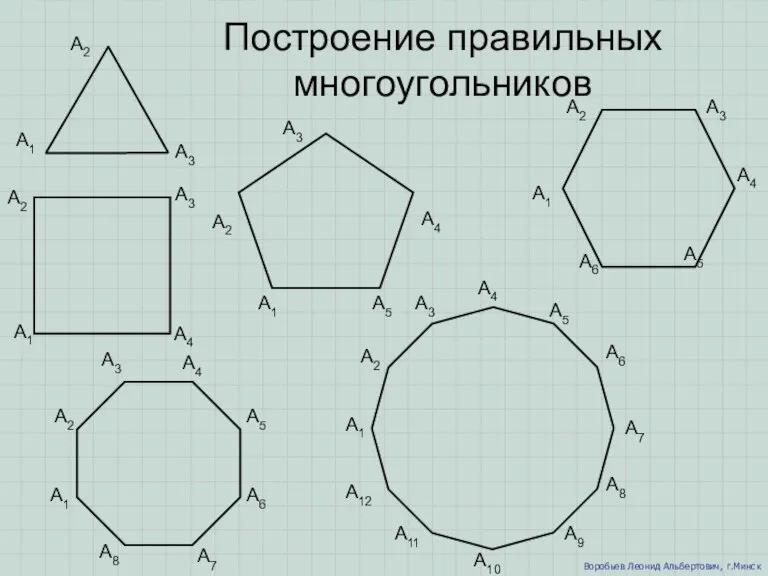 Построение правильных многоугольников
Построение правильных многоугольников Тест 3 по математике
Тест 3 по математике Рисунки из геометрических фигур
Рисунки из геометрических фигур Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Решение задач
Решение задач Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс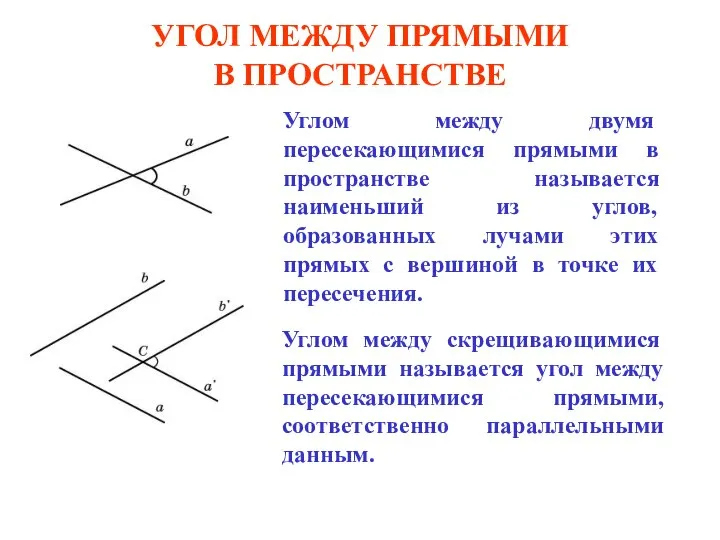 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Методы кластеризации
Методы кластеризации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей