Содержание
- 2. 1. 2. 4. 5. 3. Теорема (Необходимое и достаточное условие существование обратной матрицы):
- 4. Пример: Сделать проверку. Вывод:
- 5. Пример:
- 6. Теорема:
- 7. Пример:
- 9. Примеры: 1. 2. Решите самостоятельно
- 10. Обозначение: Определение: Определение: r(A), R(A), rang A, rg A. Рангом матрицы A называется наивысший порядок минора
- 13. Пример:
- 14. Рангом матрицы называется число ненулевых строк, в приведенной к ступенчатому виду матрицы. Теорема: Теорема: Замечание:
- 16. Скачать презентацию













 Измерение размеров деталей с помощью штангенциркуля
Измерение размеров деталей с помощью штангенциркуля Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости
Изучение нумерации числе учащимися пятых классов с легкой степенью умстенной отсталости Числовые ряды
Числовые ряды Формулы сокращенного умножения. Подготовка к СОР
Формулы сокращенного умножения. Подготовка к СОР Задачи на построение
Задачи на построение Математическая логика
Математическая логика Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ  Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Презентация на тему Радианная мера углов и дуг
Презентация на тему Радианная мера углов и дуг  Методическая разработка по математике. Тема: Треугольники
Методическая разработка по математике. Тема: Треугольники Вычитание чисел. Решение уравнений
Вычитание чисел. Решение уравнений Элементы комбинаторики
Элементы комбинаторики Контрольная работа
Контрольная работа Параллелограмм
Параллелограмм Кафедра математики МБОУ лицея № 14 г. Ставрополя
Кафедра математики МБОУ лицея № 14 г. Ставрополя Определение и способы задания числовой функции
Определение и способы задания числовой функции Математические кривые в природе и технике
Математические кривые в природе и технике Показательные уравнения и неравенства
Показательные уравнения и неравенства Понятие функции
Понятие функции Пропорция. Основное свойство пропорции
Пропорция. Основное свойство пропорции Интерпретация графиков реальной зависимости
Интерпретация графиков реальной зависимости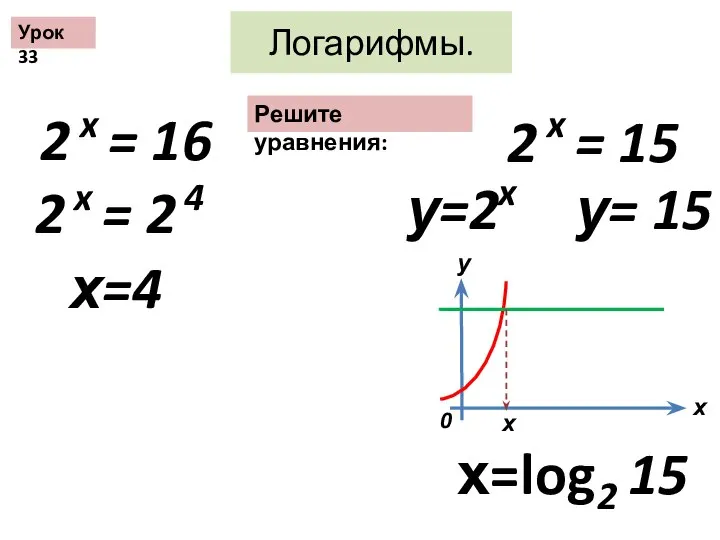 Логарифмы
Логарифмы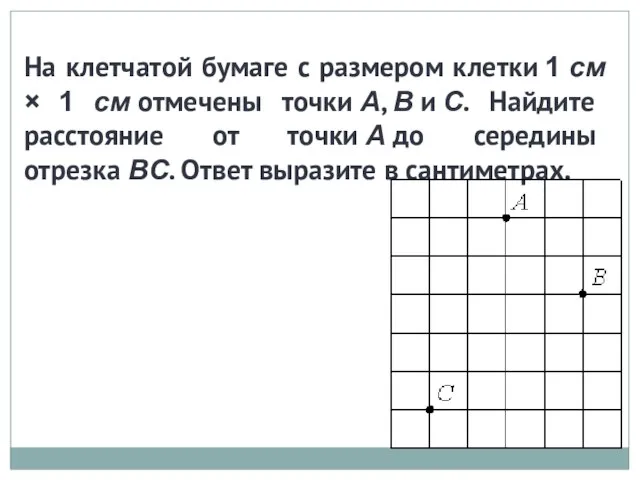 Решение задач
Решение задач Сложение и вычитание дробей
Сложение и вычитание дробей Интегральные уравнения
Интегральные уравнения