Системы линейных уравнений

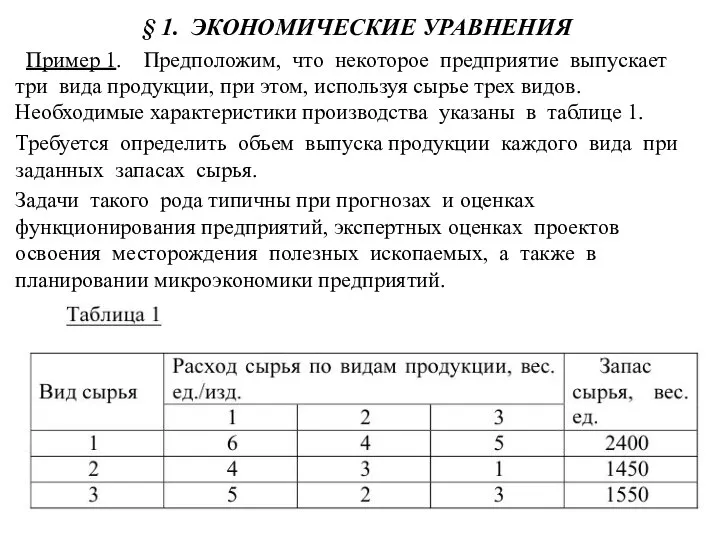
§ 1. ЭКОНОМИЧЕСКИЕ УРАВНЕНИЯ
Пример 1. Предположим, что некоторое предприятие выпускает три вида продукции, при этом, используя сырье трех видов. Необходимые характеристики производства указаны в таблице 1.
Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.
Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождения полезных ископаемых, а также в планировании микроэкономики предприятий.

Решение. Обозначим неизвестные объемы выпуска продукции через x1, x2 и x3. Тогда, при условии полного расхода запасов каждого вида сырья можно записать балансовое соотношение, которое образует систему трех уравнений с тремя неизвестными
x1=150, x2 = 250, x3 =100.
Решая эту систему уравнений любым способом, находим, что при заданных запасах сырья объемы выпуска продукции составляют по каждому виду соответствие (в условных единицах):

Лекция 7
ЭЛЕМЕНТЫ ВЕКТОРНОЙ ЛГЕБРЫ

§ 1. ПОНЯТИЕ ВЕКТОРА
Различают величины скалярные и векторные. Величина, которая полностью характеризуется одним числовым значением, выражающим отношение этой величины к соответствующей единице измерения, называется скалярной величиной или скаляром.
Таковы, например, масса тела, температура среды и т.п.
Величина, которая кроме числового значения характеризуется еще и направлением, называется векторной величиной или вектором.
К числу их относятся сила, перемещение, скорость.
Вектор определяется числом и направлением.
Векторы будем обозначать или a.
Геометрически вектор изображается
направленным отрезком пространства; при этом используется обозначение

Под модулем (длиной) вектора
понимается его численное значение, без учета направления.
Вектор, модуль которого равен нулю, называется нулевым или нуль-вектором. Направление нулевого вектора произвольно.
Два вектора и считаются равными, если они расположены на параллельных или совпадающих прямых, имеют одинаковую длину и одинаково направлены.
Мы условимся не различать равные векторы и, таким образом, приходим к понятию свободного вектора. Иными словами, свободный вектор допускает перенос его в любую точку пространства, при условии сохранения длины и направления. В частности, для свободных векторов всегда можно обеспечить их общую начальную точку.

§ 2. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
Сумма векторов
Суммой нескольких векторов, например, называется вектор
по величине и направлению равный замыкающей пространственной ломаной линии, построенной на данных векторах.
Для случая двух векторов их суммой является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
Так как в любом треугольнике длина одной стороны не превышает суммы длин двух других сторон, то из рис. следует

Для случая трех векторов их суммой является диагональ ОМ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Легко проверить, что для
векторного сложения справедливы
следующие свойства:
1) переместительное свойство:
2) сочетательное свойство:
Для каждого вектора существует противоположный вектор, имеющий ту же длину, но противоположное направление

По правилу параллелограмма имеем , где 0 - нуль-вектор. Легко проверить, что
Разность векторов
Под разностью векторов a и b будем понимать вектор
d = a - b , такой что b + d = a .
Отметим, что в параллелограмме, построенном на данных векторах a и b , их разностью является соответственно направленная вторая диагональ параллелограмма.
Легко проверить, что справедливо следующее правило вычитания:

Умножение вектора на скаляр.
Определение. Произведением вектора a на скаляр k
называется вектор, имеющий длину b =|k| a , направление, которого:
1) совпадает с направлением вектора a , если k > 0;
2) противоположно ему, если k < 0;
3) произвольно, если k = 0.
Нетрудно убедиться, что данная векторная операция обладает следующими свойствами:

Если ненулевой вектор a разделить на его длину a =|a| , то мы получим единичный вектор e , так называемый орт, того же направления: e = a / a
Отсюда имеем стандартную формулу вектора: a = ae.
§ 3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Определение. Два вектора a и b называются коллинеарными, если они расположены или на параллельных прямых, или же на одной и той же прямой.
Так как направление нулевого вектора произвольно, то можно считать, что нулевой вектор коллинеарен любому вектору.
Справедлива Теорема 1. Два ненулевых вектора a и b коллинеарны тогда и только тогда, когда они пропорциональны,
т. е. b = ka, где k — скаляр.

Пусть векторы a и b ( а ≠ 0, b ≠ 0 ) коллинеарны и e,e′— их орты. Имеем a = ae и b = be′, где e′ = ±e .
Знак плюс соответствует векторам a и b одинакового направления, а знак минус — векторам a и b противоположного направления.
Тогда получаем, что b = ±be = ±b/a (ae)= ± (b/a) a
Отсюда вытекает формула b = ka где k = ±b / a .
Если выполнено равенство, то коллинеарность векторов a и b непосредственно следует из смысла умножения вектора на скаляр.
Определение. Три вектора a, b и c называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Тогда можно сказать также, что векторы a, b и c компланарны тогда и только тогда, когда после приведения их к общему началу они лежат в одной плоскости.

По смыслу определения тройка векторов, среди которых имеется хотя бы один нулевой вектор, компланарна.
Теорема 2. Три ненулевых вектора a, b и c компланарны тогда и только тогда, когда один из векторов является линейной комбинацией других, т. е., например c = ka + lb .
Доказательство. 1)Пусть векторы a, b и c компланарны, расположены в плоскости Р и имеют общую точку приложения О.
Предположим сначала, что эти векторы не все попарно коллинеарны, например, векторы a и b неколлинеарны. Тогда, производя разложение вектора c в сумму векторов ca и cb коллинеарных,
соответственно, векторам a и b, будем иметь, c= ca + cb = ka+lb где k и l — соответствующие скаляры.