Обратные тригонометрические функции

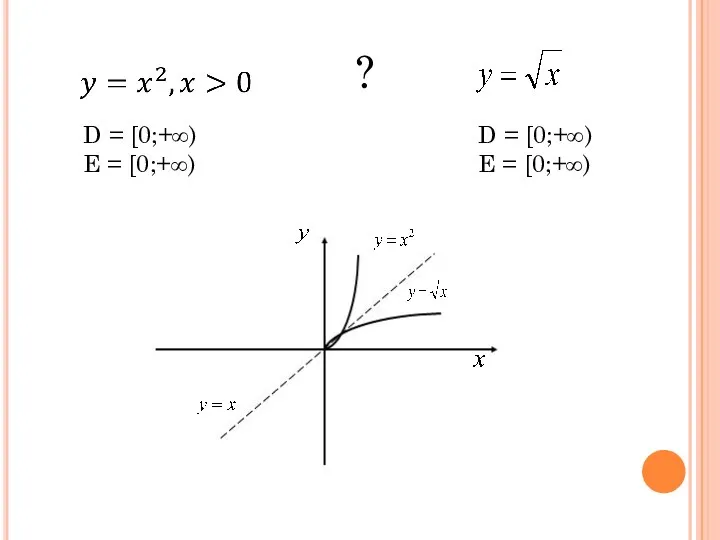
D = [0;+∞)
E = [0;+∞)
D = [0;+∞)
E = [0;+∞)
?

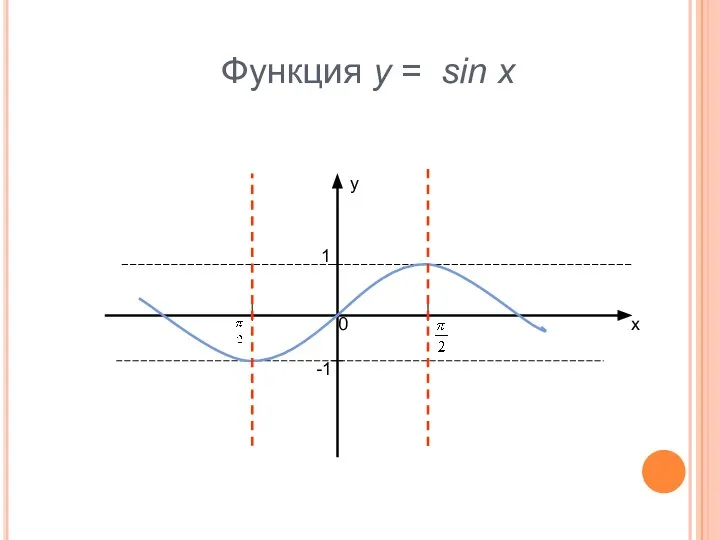
Функция у = sin x
у
х
1
-1
0

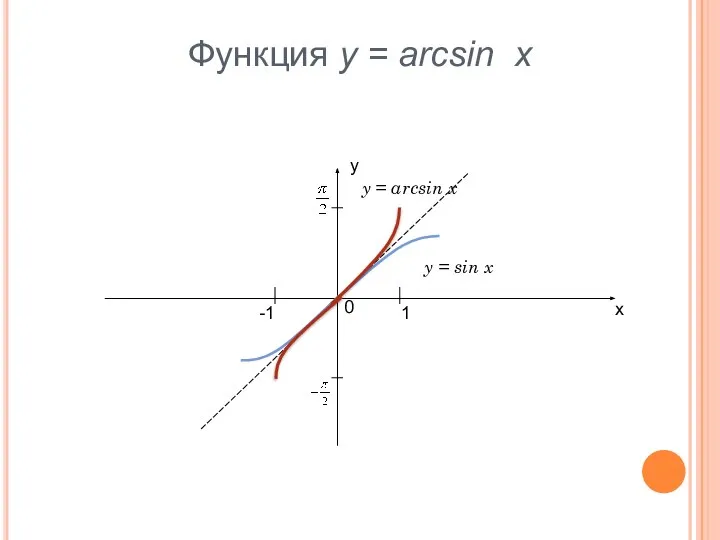
Функция y = arcsin x
у
х
0
-1
1
y = sin x
y = arcsin x

Свойства функции y = arcsin x
D(f) = [-1;1].
E(f) = [- ; ].
Функция является нечётной:
arcsin(- x) = - arcsin x.
Функция возрастает.
Функция непрерывна.

Определение 1.
Если |a| ≤ 1, то
sin t = a,
arcsin a = t
- ≤ t ≤ ;
sin (arcsin a)= a

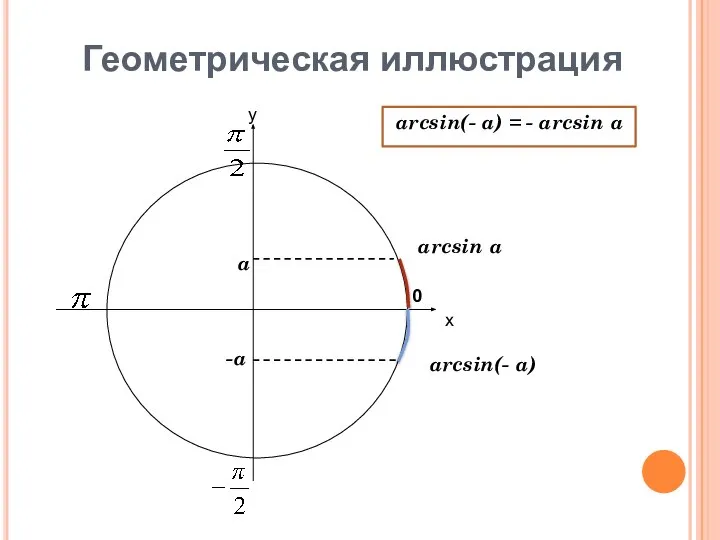
Геометрическая иллюстрация
х
у
0
arcsin a
arcsin(- a)
a
-a
arcsin(- a) = - arcsin a

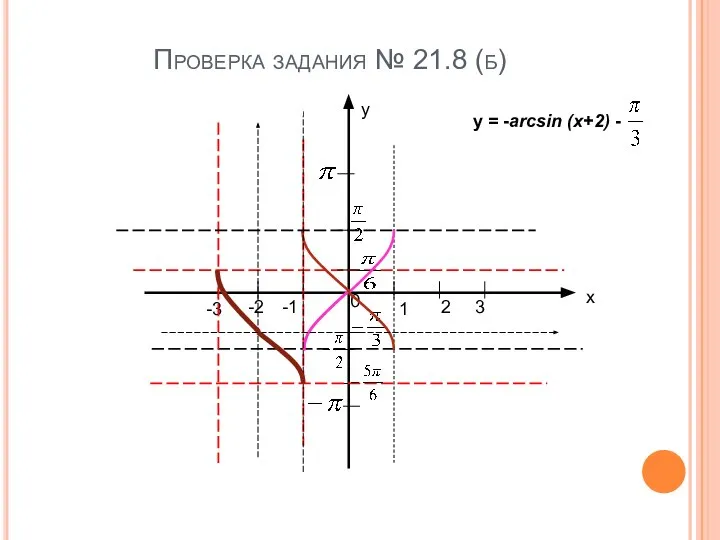
Проверка задания № 21.8 (б)
х
у
-1
1
2
3
-2
-3
0
у = -arcsin (x+2) -

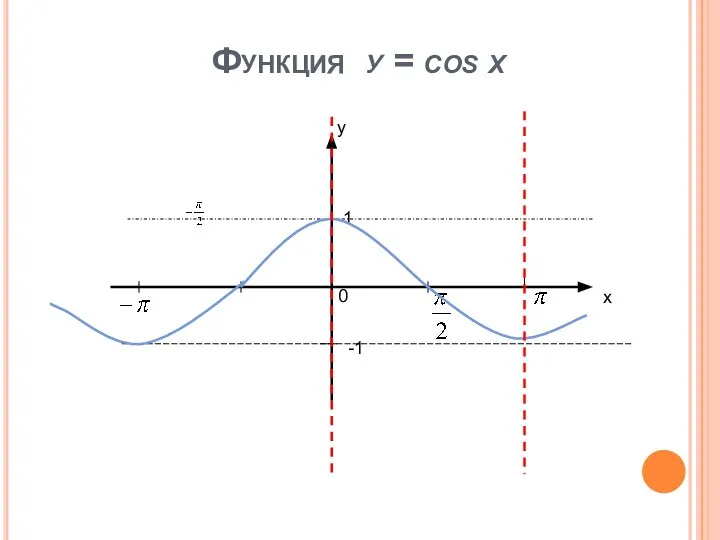
Функция у = cos x
х
у
0
1
-1

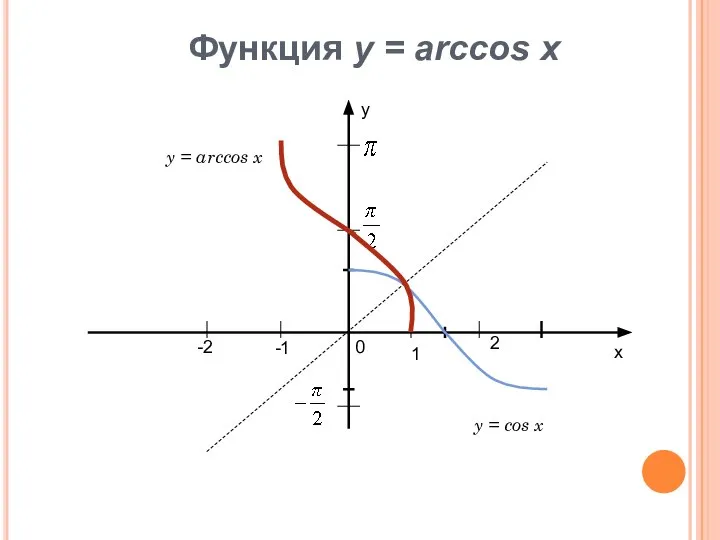
х
у
1
2
-1
-2
0
Функция у = arccos x
y = arccos x
y = cos x

Свойства функции y = arccos x
D(f) = [-1;1].
E(f) = [0;π ].
Функция не является ни чётной, ни нечётной.
Функция убывает.
Функция непрерывна.

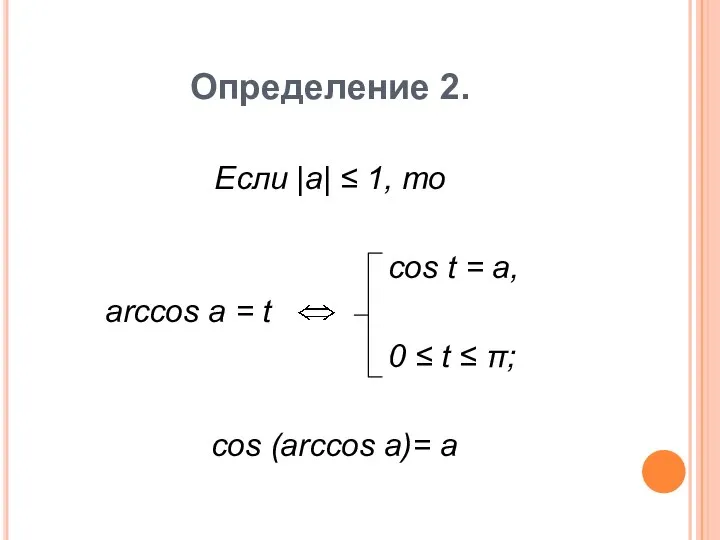
Определение 2.
Если |a| ≤ 1, то
cos t = a,
arccos a = t
0 ≤ t ≤ π;
cos (arccos a)= a

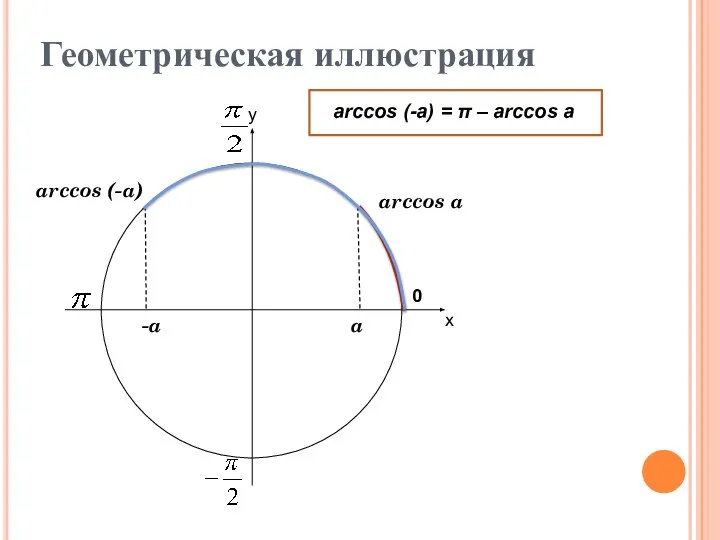
х
у
0
Геометрическая иллюстрация
arccos a
arccos (-a)
-a
a
arccos (-a) = π – arccos a

Вычислите:
а) sin (arcsin )
б) cos (arcsin )
в) tg (arcsin )

Домашнее задание
Учебник §21п.1,2 (учить опр., свойства, формулы), п.3,4(конспект)
Задачник №21.26а), №21.17.

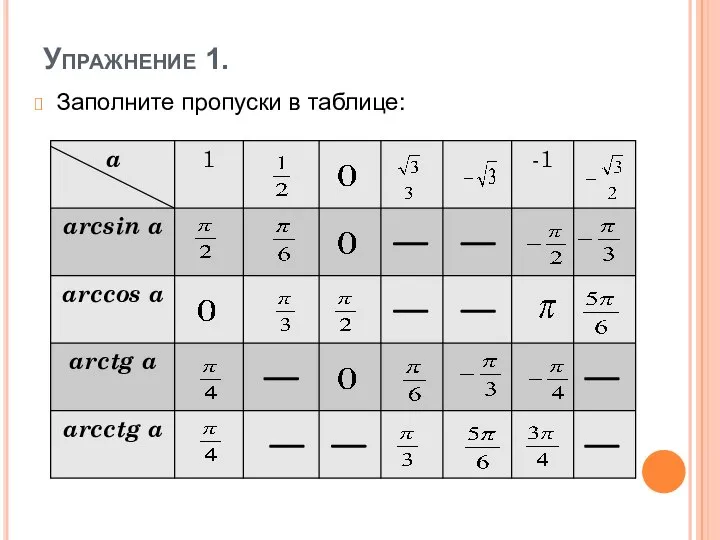
Упражнение 1.
Заполните пропуски в таблице:

Упражнение 2
Найдите область определения и область значений выражений:

Упражнение 3
Имеет ли смысл выражение:
arcsin(-1/2) arccos arcsin(3 - )
да нет нет
arcsin1,5 arccos(- +1 ) arccos
нет да да

Упражнение 4
Сравните числа:
<
>
<
<

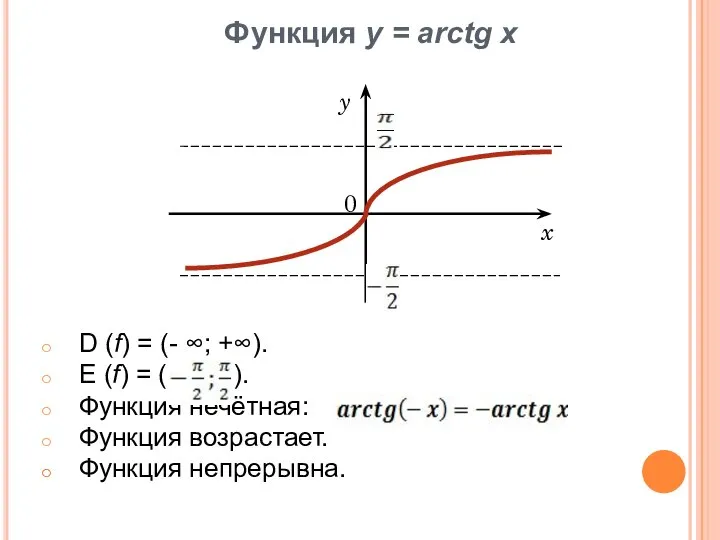
Функция у = arctg x
D (f) = (- ∞; +∞).
E (f) = ( ).
Функция нечётная:
Функция возрастает.
Функция непрерывна.
x
0
y

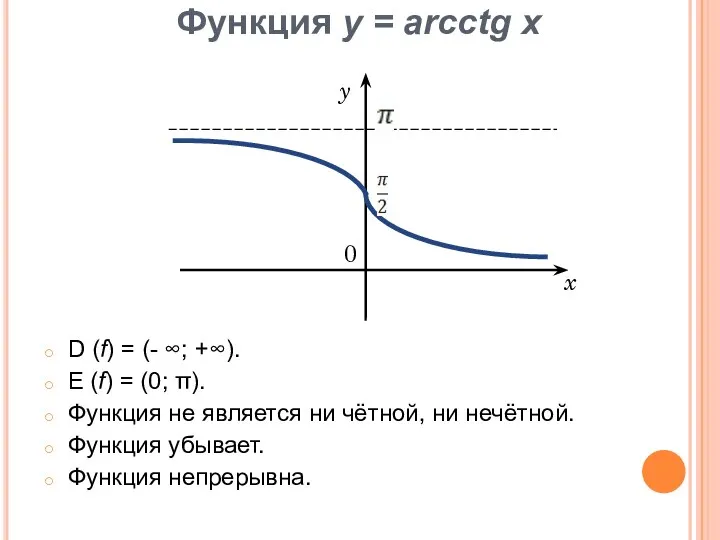
Функция у = arсctg x
D (f) = (- ∞; +∞).
E (f) = (0; π).
Функция не является ни чётной, ни нечётной.
Функция убывает.
Функция непрерывна.
y
x
0

Тригонометрические операции над обратными
тригонометрическими функциями

Домашнее задание
1) §21(л.1,2,3,4 – повт., п. 5 – чит.)
2) Дано . Выразить через остальные аркфункции.
3) Вычислить: а) ; б) .
4) №21.52 а)б) (по желанию).
.

Упражнение 5
а) б) в) г)
а) б) в) г)
а) б) в) г)
а) б) в) г)
а) б) в) г)
а) б) в) г)

Упражнение 6

Упражнение 7
Найдите наименьшее значение a, при котором существует выражение
Решение.
Значит, наименьшее значение a = 0,25.
- 4 ≤ - 8a ≤ - 2
– 1 ≤ 3 – 8a ≤ 1
0,25 ≤ a ≤ 0,5