Содержание
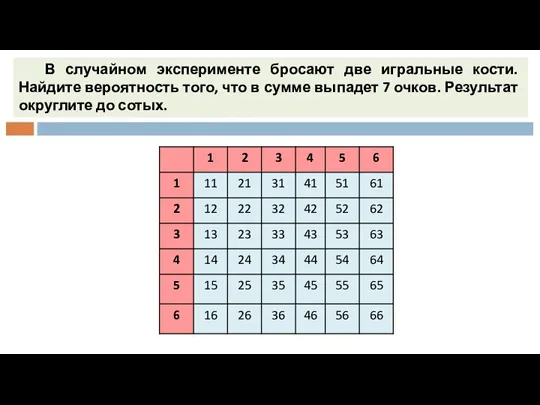
- 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
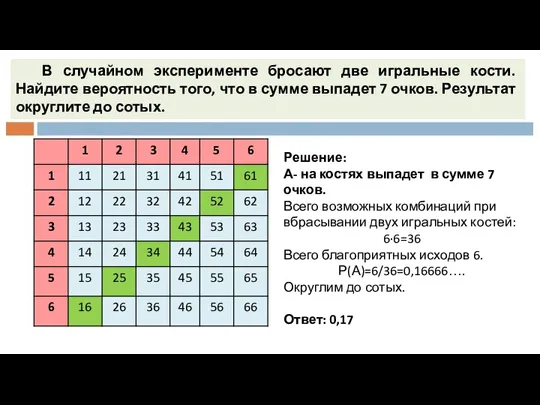
- 3. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
- 4. У Дины в копилке лежит 7 рублёвых, 5 двухрублёвых, 6 пятирублёвых и 2 десятирублёвых монеты. Дина
- 5. У Дины в копилке лежит 7 рублёвых, 5 двухрублёвых, 6 пятирублёвых и 2 десятирублёвых монеты. Дина
- 6. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите
- 7. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите
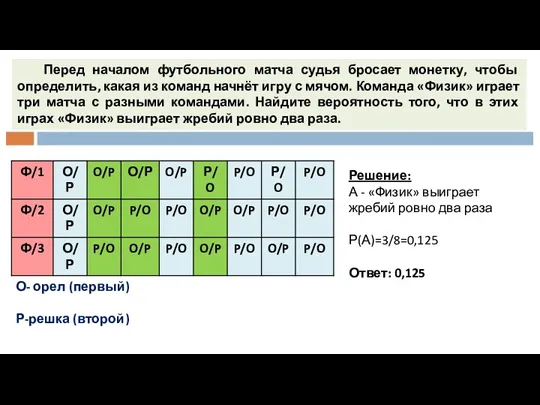
- 8. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом.
- 9. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом.
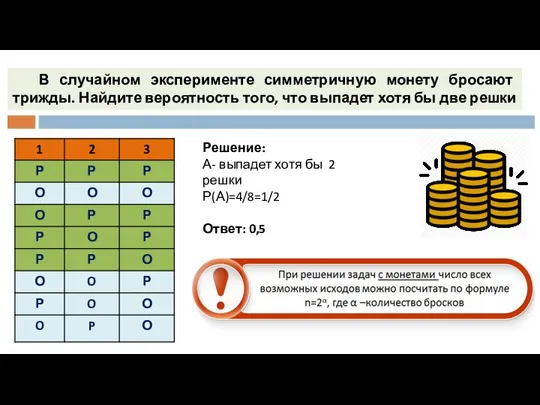
- 10. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки
- 11. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки
- 12. Математический диктант Случайные события. Вероятность случайного события Вариант 1
- 13. Математический диктант Случайные события. Вероятность случайного события Вариант 2
- 15. Критерии оценивания
- 17. Теоремы сложения и умножения вероятностей
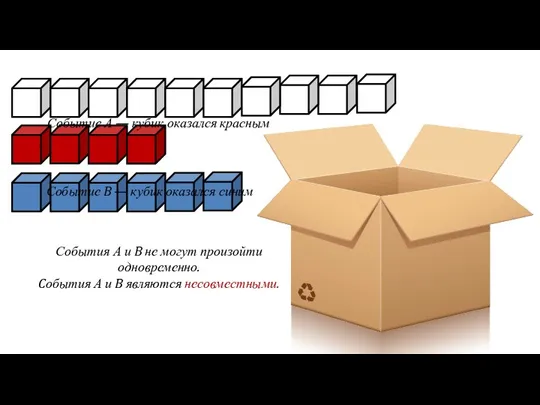
- 18. Событие А — кубик оказался красным Событие B — кубик оказался синим События А и B
- 19. Два события называют НЕСОВМЕСТНЫМИ, если в одном и том же испытании они не могут произойти одновременно,
- 20. Теорема сложения вероятностей: Вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей
- 21. Пример 1 Есть 10 экзаменационных билетов. Ученик вытянул один из них. Какова вероятность того, что номером
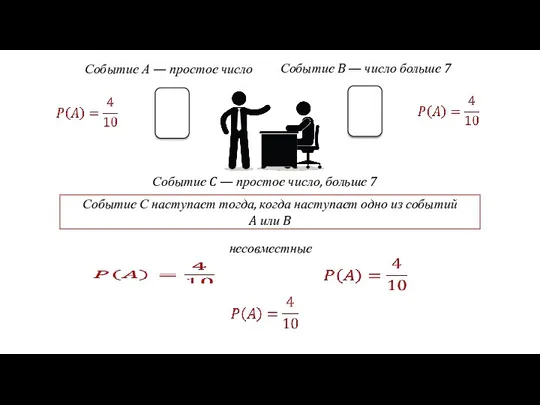
- 22. Событие А — простое число Событие B — число больше 7 Событие C — простое число,
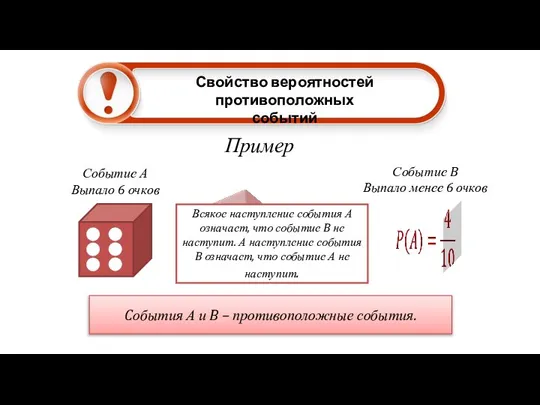
- 23. Пример Свойство вероятностей противоположных событий Событие А Выпало 6 очков Событие B Выпало менее 6 очков
- 24. Событие А Выпало 6 очков Событие B Выпало менее 6 очков 1 благоприятный исход из 6
- 26. Пример Какова вероятность того, что сумма очков, выпавших на двух кубиках, меньше 9? Общее число равновозможных
- 27. Два события называют СОВМЕСТНЫМИ, если в одном и том же испытании они могут произойти одновременно, то
- 28. Теорема сложения вероятностей двух совместных событий: Если события A и B совместны, то вероятность появления одного
- 29. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате
- 30. Вероятность первого события А – «кофе закончится в первом автомате» также как и вероятность второго события
- 31. Рассмотрим, как можно вычислить вероятность события, состоящего в совместном появлении двух независимых событий. Два события называются
- 32. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий Р(А·B)=P(A)·P(B) Теорема
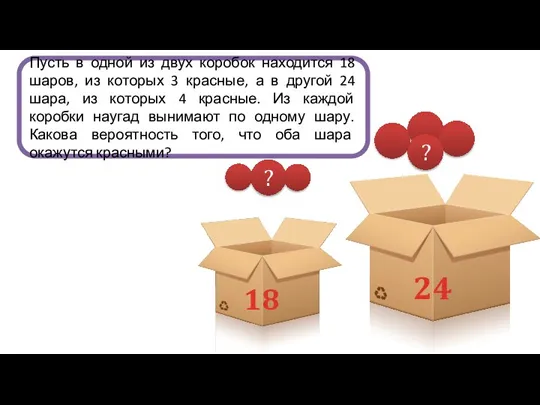
- 33. ? ? 18 24 Пусть в одной из двух коробок находится 18 шаров, из которых 3
- 34. Событие А из первой коробки вынимают красный шар Событие B из второй коробки вынимают красный шар
- 35. Два события называются ЗАВИСИМЫМИ, если одно из них влияет на вероятность появления другого.
- 36. Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на
- 37. В ящике 6 белых и 8 чёрных шаров. Из ящика вынули два шара (не возвращая вынутый
- 38. P (AB)= P (A)· PА(B)= (6/ 14) ·(5 / 13)= 30/182. Ответ: 0,16 А – «первый
- 39. Домашнее задание Задачник Башмакова М.И. упр. 11.16, 11.17, 11.18, 11.21,
- 42. Скачать презентацию































 Линейные уравнения
Линейные уравнения Тайна Египетского треугольника
Тайна Египетского треугольника Презентация на тему О числах
Презентация на тему О числах  Методы измерений в квалиметрии
Методы измерений в квалиметрии Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Векторы. Тест
Векторы. Тест Действия с десятичными дробями
Действия с десятичными дробями Понятие логарифма
Понятие логарифма Презентация на тему Решение задач по математике
Презентация на тему Решение задач по математике  Измерение отрезков и углов
Измерение отрезков и углов Все действия с рациональными числами
Все действия с рациональными числами Задания части 1. Вступительные испытания
Задания части 1. Вступительные испытания Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Алгоритм умножения
Алгоритм умножения Иррациональные уравнения
Иррациональные уравнения Таблица истинности
Таблица истинности Закрепление материала Больше, меньше, поровну (2 занятие)
Закрепление материала Больше, меньше, поровну (2 занятие) Математические ребусы. 2 класс
Математические ребусы. 2 класс Производная произведения двух функций
Производная произведения двух функций Математика здесь!
Математика здесь! Число и цифра 5
Число и цифра 5 Презентация на тему Сравнение углов
Презентация на тему Сравнение углов  Своя игра (4)
Своя игра (4) Единицы объёма. Задания
Единицы объёма. Задания Выдающиеся российские математики. Урок-лекция, 5- 11 кл
Выдающиеся российские математики. Урок-лекция, 5- 11 кл Презентация на тему Разность и её значение (1 класс)
Презентация на тему Разность и её значение (1 класс)  Задачи, решаемые геометрическим моделированием
Задачи, решаемые геометрическим моделированием Занимательная математика.Игры с кубиками, 1 класс
Занимательная математика.Игры с кубиками, 1 класс