Содержание
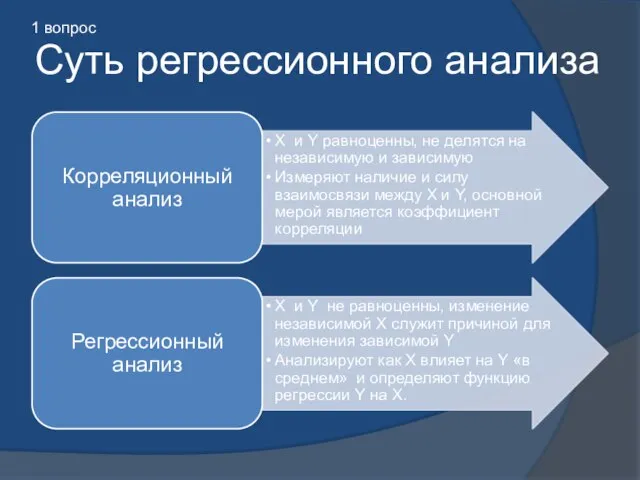
- 2. Суть регрессионного анализа 1 вопрос
- 3. Цель регрессионного анализа Термин «регрессия» был введен Фрэнсисом Гальтоном в конце 19 века.
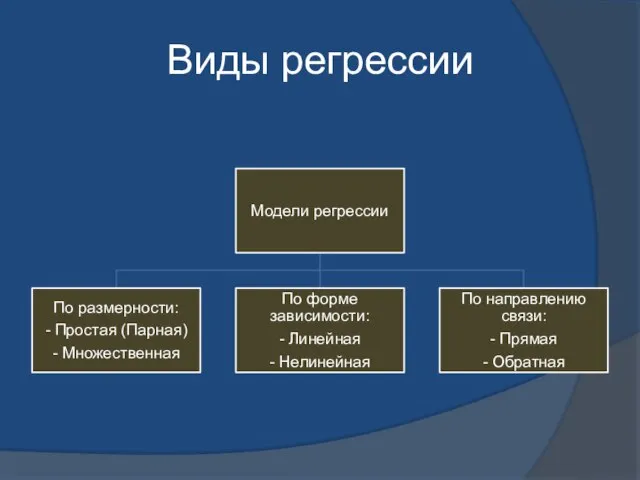
- 4. Виды регрессии
- 5. Простая (парная) регрессия представляет собой модель, где среднее значение зависимой переменной Y рассматривается как функция одной
- 6. Спецификация модели - формулирование вида модели, исходя из соответствующей теории связи между переменными. Исследование начинается с
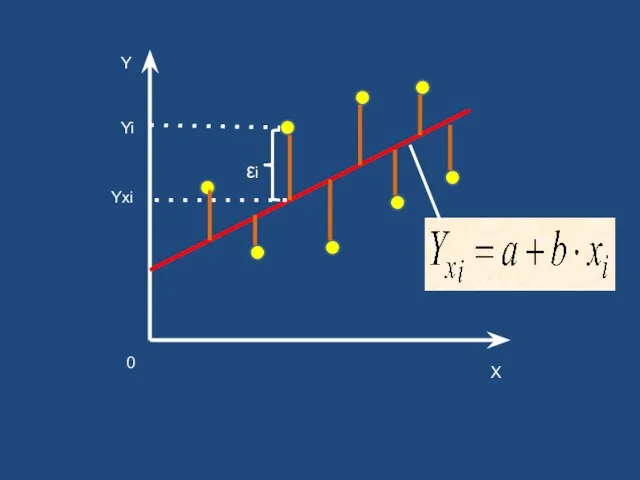
- 7. Спецификация линейной модели парной регрессии Yi - фактическое значение зависимой переменной Y Yxi - теоретическое (среднее)
- 8. Эмпирическое уравнение линейной регрессии Yxi - теоретическое (среднее) значение зависимой переменной Y, найденное из уравнения регрессии
- 9. Теоретическая линейная модель парной регрессии α – свободный коэффициент β - коэффициент регрессии εi – случайное
- 10. Типы ошибок в регрессии
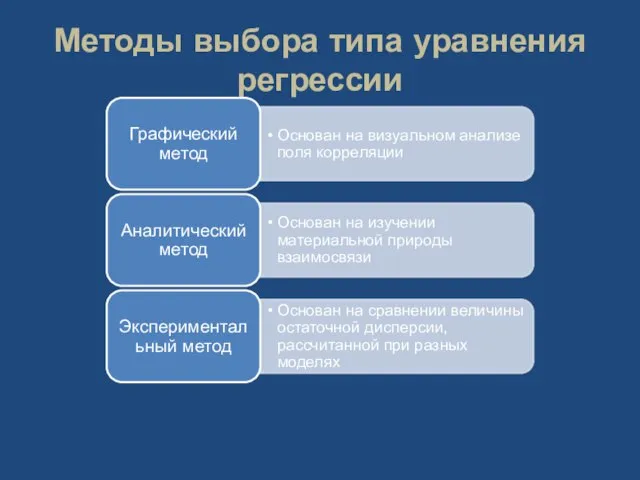
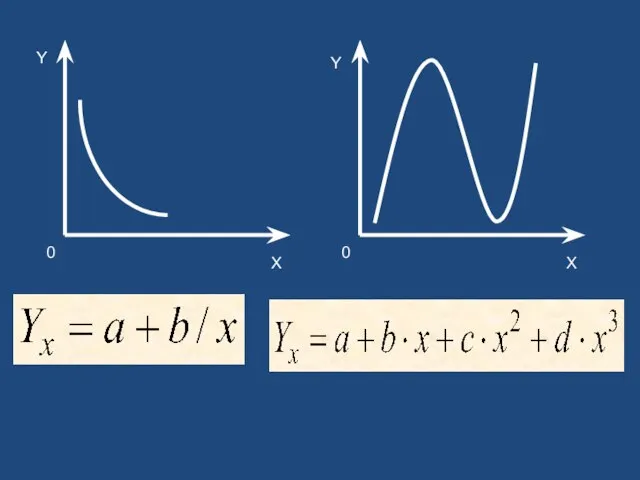
- 11. Методы выбора типа уравнения регрессии
- 12. X Y X Y 0 0
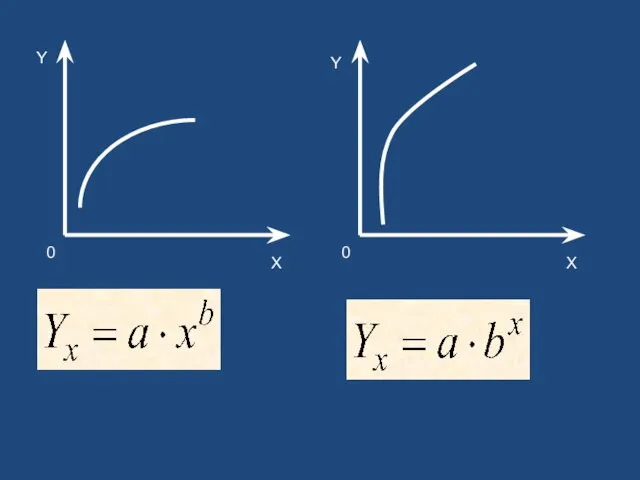
- 13. Y X X Y 0 0
- 14. Y X X Y 0 0
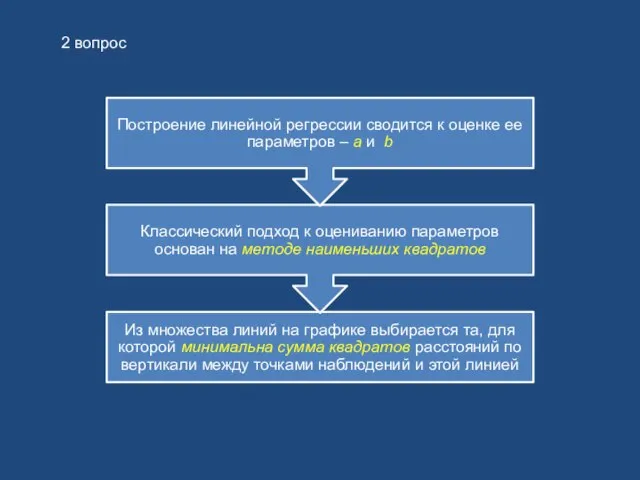
- 15. 2 вопрос
- 16. Y X 0 Yxi Yi εi
- 17. Суть метода наименьших квадратов (МНК) - оценки параметров таковы, что сумма квадратов отклонений фактических значений зависимой
- 18. Оценка параметров регрессии
- 20. Скачать презентацию







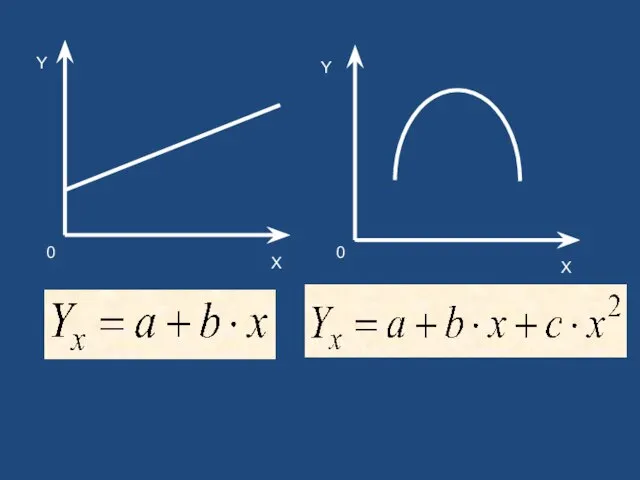


 Случайные события
Случайные события Решите неравенства
Решите неравенства Параллельность прямых и плоскостей в пространстве с решением
Параллельность прямых и плоскостей в пространстве с решением Свойства функций. 9 класс
Свойства функций. 9 класс Интересные факты про математику
Интересные факты про математику Скалярное произведение векторов. тест
Скалярное произведение векторов. тест Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств
Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств Математические головоломки. Математика вокруг нас
Математические головоломки. Математика вокруг нас Признаки параллелограмма
Признаки параллелограмма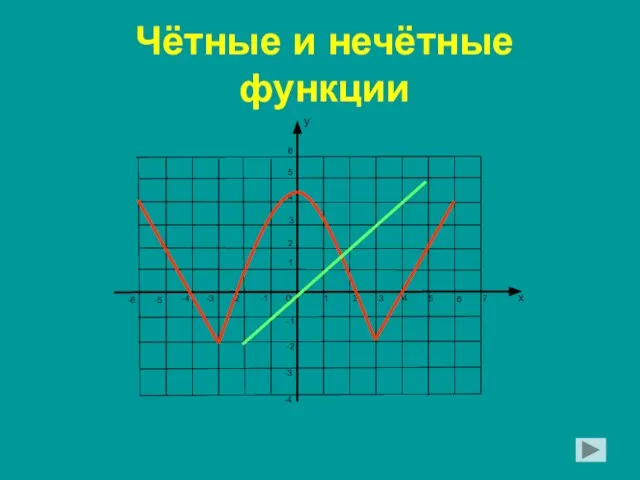 Презентация на тему Чётные и нечётные функции
Презентация на тему Чётные и нечётные функции  Решение треугольников. 9 класс
Решение треугольников. 9 класс Правильные многогранники. Моделирование многогранников
Правильные многогранники. Моделирование многогранников Угол между прямой и плоскостью
Угол между прямой и плоскостью Подобие треугольников. Второй признак
Подобие треугольников. Второй признак Дробь. Подготовка к олимпиадам
Дробь. Подготовка к олимпиадам Равносильные преобразования
Равносильные преобразования Задача по математике (4 класс, задание 85.1)
Задача по математике (4 класс, задание 85.1) Музыкалық аспаптарға
Музыкалық аспаптарға Презентация на тему Неравенства с двумя переменными
Презентация на тему Неравенства с двумя переменными  Пределы
Пределы Выражение в инфиксной форме. Выражение в постфиксной форме
Выражение в инфиксной форме. Выражение в постфиксной форме Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Математическое и сенсорное развитие детей раннего возраста
Математическое и сенсорное развитие детей раннего возраста Применение функциональных зависимостей в реальных процессах и явлениях
Применение функциональных зависимостей в реальных процессах и явлениях Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ  Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода Презентация на тему ГИА 2013 Модуль «Геометрия» № 9
Презентация на тему ГИА 2013 Модуль «Геометрия» № 9