Содержание
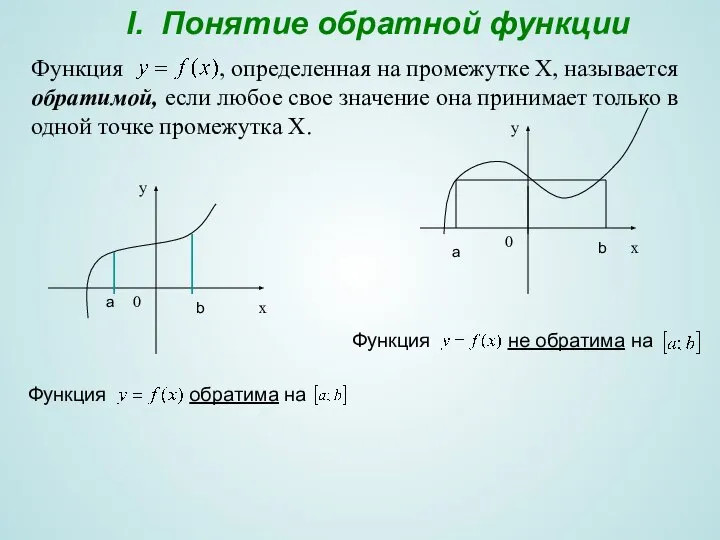
- 2. I. Понятие обратной функции Функция , определенная на промежутке Х, называется обратимой, если любое свое значение
- 3. Теорема. Если функция строго монотонна на промежутке Х, то она обратима на этом промежутке. Доказательство. Пусть
- 4. Пусть обратимая функция определена на промежутке Х, а областью значений ее является промежуток Y. Поставим в
- 5. Алгоритм получения обратной функции 1) Убедиться в том, что функция обратима на Х. 2) Из уравнения
- 6. Лекция Обратные тригонометрические функции
- 7. Тест 10 минут Критерии Оценка «5» - 5 баллов Оценка «4» - 4 балла Оценка «3»
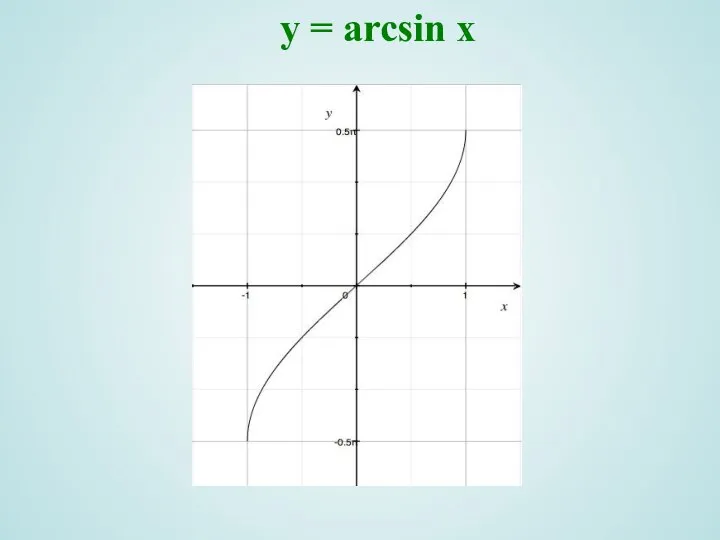
- 8. y = arcsin x
- 9. y = arcsin x Область определения ; , 2) Область значений ; 3) Функция нечетная arcsin
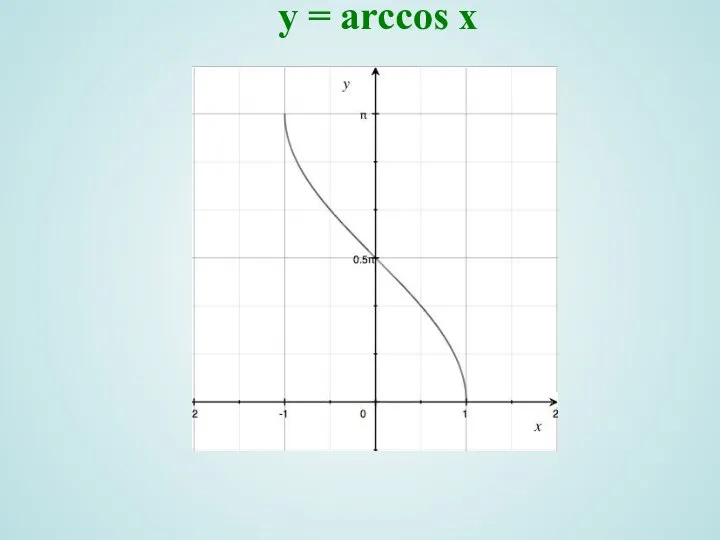
- 10. y = arccos x
- 11. y = arccos x Область определения ; , 2) Область значений ; 3) Функция не обладает
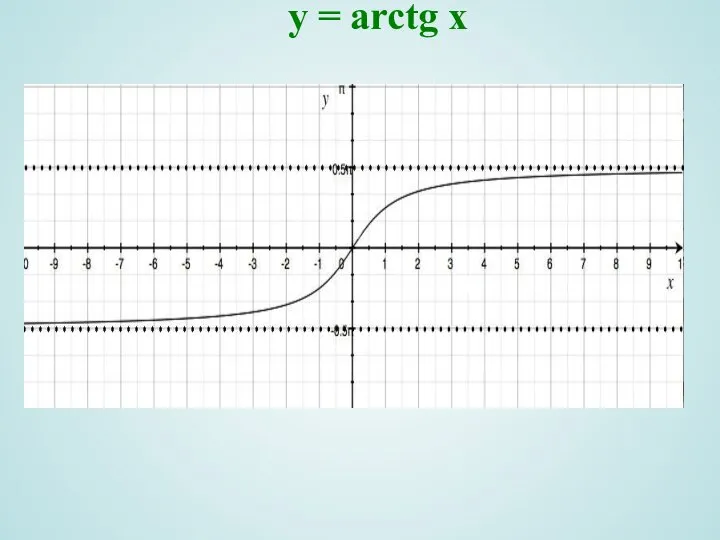
- 12. y = arctg x
- 13. y = arctg x Область определения D(y)=R ; , 2) Область значений ; 4) Функция непериодическая
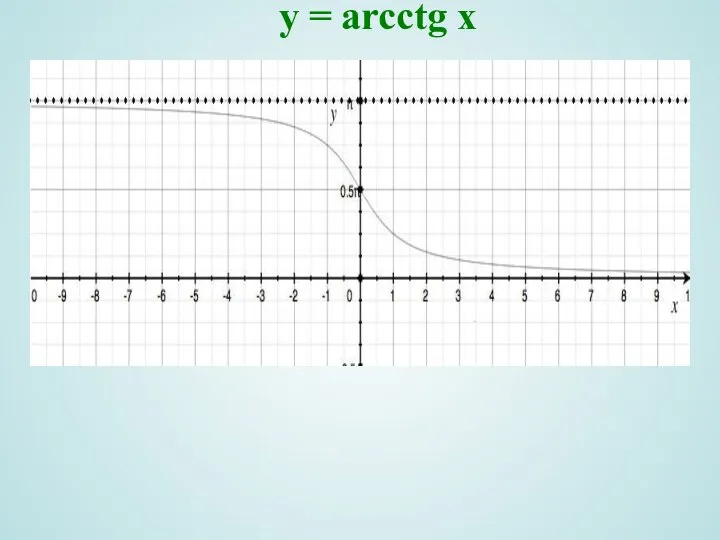
- 14. y = arcctg x
- 15. y = arcсtg x Область определения D(y)=R ; , 2) Область значений ; 4) Функция непериодическая
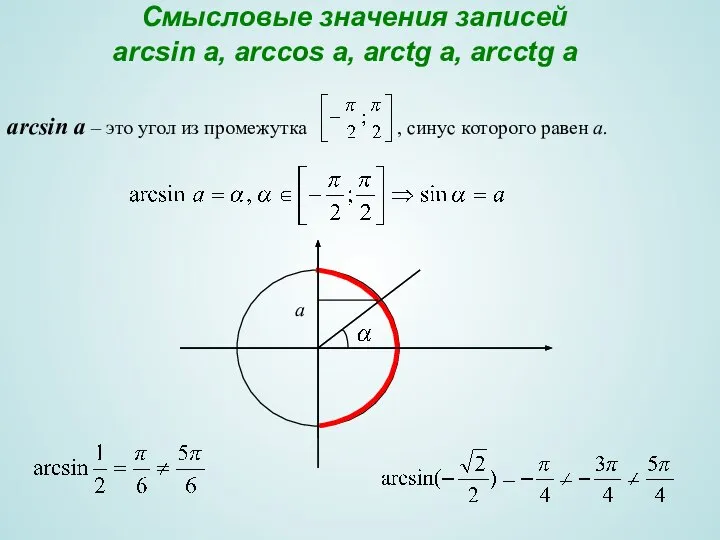
- 16. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrcsin a – это угол
- 17. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrccos a – это угол
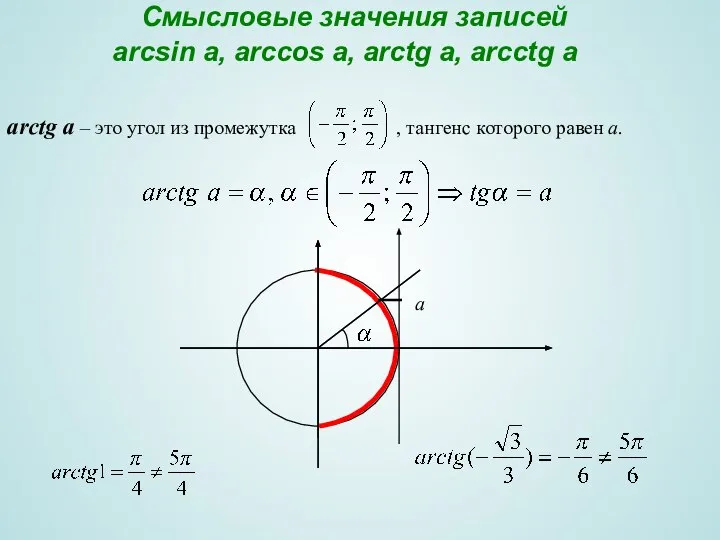
- 18. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrctg a – это угол
- 19. Смысловые значения записей arcsin a, arccos a, arctg a, arcctg a аrcсtg a – это угол
- 20. Основные свойства обратных тригонометрических функций
- 22. Скачать презентацию












 Четные и нечетные числа
Четные и нечетные числа Эталон и его назначение
Эталон и его назначение Математика и физика здоровья
Математика и физика здоровья Векторы на плоскости
Векторы на плоскости Запись решения задачи по действиям
Запись решения задачи по действиям Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения
Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения Задача о семи Кенигсбергских мостах
Задача о семи Кенигсбергских мостах Решение задач на проценты
Решение задач на проценты Сумма углов в треугольнике
Сумма углов в треугольнике Анимационная презентация для подготовки к ВПР
Анимационная презентация для подготовки к ВПР Нахождение числа по его дроби
Нахождение числа по его дроби Квадратичная функция. Её свойства и график
Квадратичная функция. Её свойства и график Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Критерий Пирсона
Критерий Пирсона Золотое сечение в природе
Золотое сечение в природе Наборы из нулей и единиц. Дискретный анализ. Лекция 2
Наборы из нулей и единиц. Дискретный анализ. Лекция 2 Презентация на тему Занимательная математика (4 класс)
Презентация на тему Занимательная математика (4 класс)  Численное решение дифференциальных уравнений
Численное решение дифференциальных уравнений Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Тема 4. Производная функции
Тема 4. Производная функции priznaki_parallelogramma (2)
priznaki_parallelogramma (2) Чтение графика функции
Чтение графика функции Решение стереометрических задач методом координат
Решение стереометрических задач методом координат Математика вокруг нас. Геометрия на столе с ножницами и без
Математика вокруг нас. Геометрия на столе с ножницами и без Деление окружности на равные части
Деление окружности на равные части Решение по готовы чертежам по теме: Длина окружности, 9 класс
Решение по готовы чертежам по теме: Длина окружности, 9 класс