Квадратичная функция. Её свойства и график

y= ax2 +bx + c
где: a,b,c – числа
Х – независимая переменная
а 0
Определение квадратичной функции
Квадратичной функцией называется функция , которую можно задать формулой вида:

Алгоритм построения параболы у = ах2 + bх + с :
Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось симмертрии.
Определить направление ветвей параболы.
Найти координаты еще нескольких точек , принадлежащих искомому графику ( в частности, координаты точки пересечения параболы с осью у и нули функции, если они существуют).
Отметить на координатной плоскости найденные точки и соединить их плавной линией.
График любой квадратичной функции – парабола.

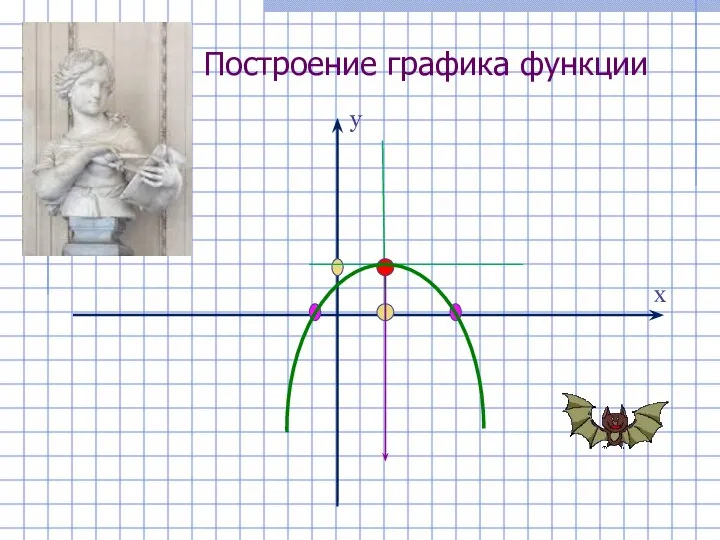
Построение графика функции
у
х

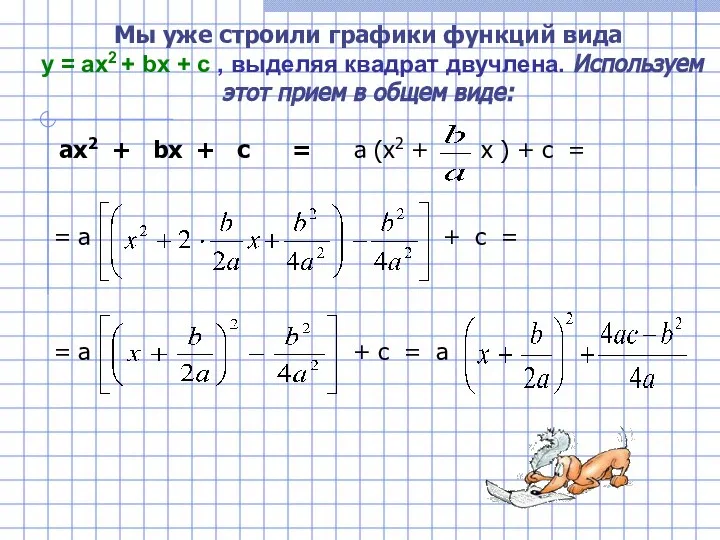
Мы уже строили графики функций вида
у = ах2 + bх + с , выделяя квадрат двучлена. Используем этот прием в общем виде:
ах2 + bx + с = а (х2 + x ) + с =
= а + с =
= а + с = а

Нам удалось преобразовать квадратный трехчлен к приведенному виду у = а ( х – x0)2 + y0,
Теперь если , то получаем ,
чтобы построить график функции у = ах2 + bx + с,
надо выполнить параллельный перенос параболы у = ах2, чтобы вершина оказалась в точке ( x0 ; y0 )

Осью параболы будет прямая
х = -
Вершина параболы - ( х0; уо) ,
где : хо = - у0 =
Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из параболы
у = ах2 параллельным переносом.
.
-
Таким образом, мы доказали теорему:

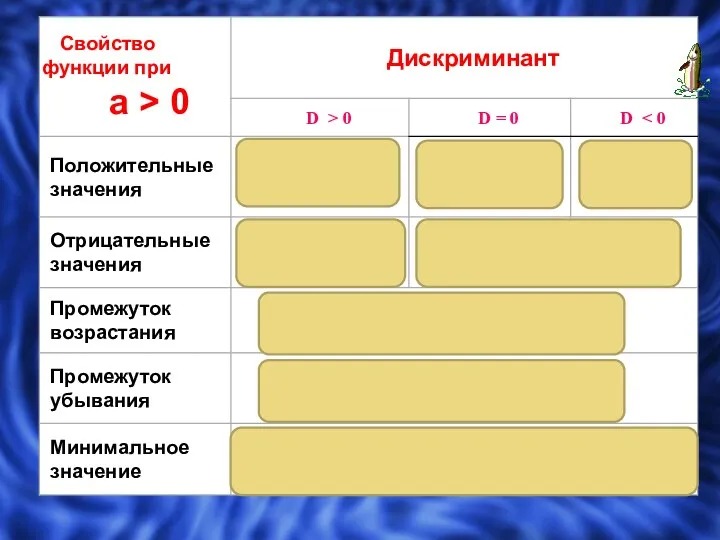
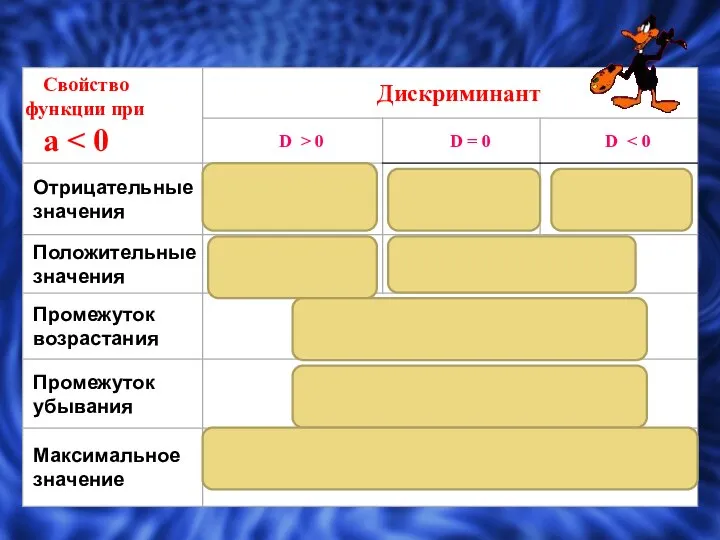
Свойства квадратичной функции
Многие свойства квадратичной функции зависят от значения дискриминанта.
Функция непрерывна
Множество значений при a>0 -
Множество значений при a<0 -

Вспоминаем :
Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение
b2 – 4ac
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D > 0
D = 0
D < 0

если дискриминант больше нуля, то парабола пересекает ось абсцисс в двух точках, если дискриминант равен нулю, то парабола касается оси абсцисс,
если дискриминант меньше нуля, то парабола не пересекает ось абсцисс,
если старший коэффициент квадратного трёхчлена (а) равен нулю, то графиком функции является не парабола, а прямая; (и соответствующее уравнение надо решать не как квадратное, а как линейное),
абсцисса вершины параболы равна

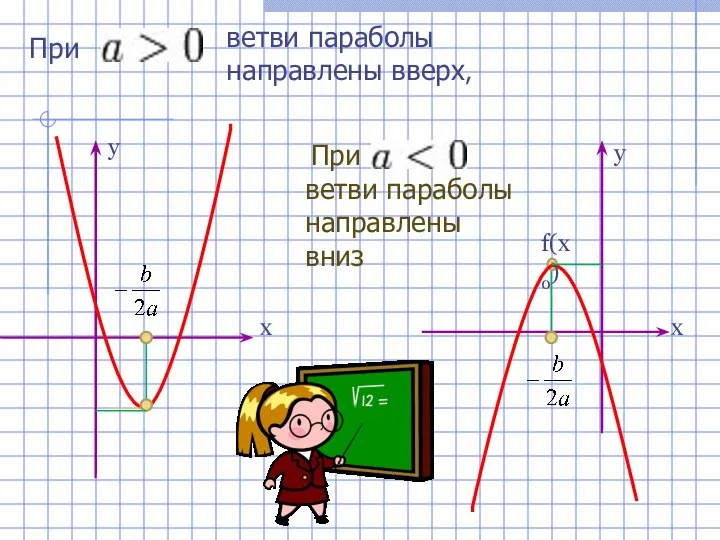
При
-
ветви параболы направлены вверх,
При
ветви параболы направлены вниз
f(x0)
х
х
у
у

Литература
1. Методическая разработка урока «Функция у = ах2 + bx + с, ее свойства и график».УМК «Алгебра, 8 класс» А.Г. Мордкович.Гл. 2 «Квадратичная функция».
2. Мерзляк А.Г.Полонский В.Б. Якир М.С. Алгебра:Учебник для 9 кл. общеобразовательных учебных заведений.- Х. Гимназия, 2009