Задача о семи Кенигсбергских мостах

Задача о семи Кенигсбергских мостах
Старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды.

Задача о семи Кенигсбергских мостах
Впервые была решена в 1736 году математиком Леонардом Эйлером, доказавшим, что это невозможно, и изобретшим таким образом эйлеровы циклы.

Решение задачи по Леонарду Эйлеру
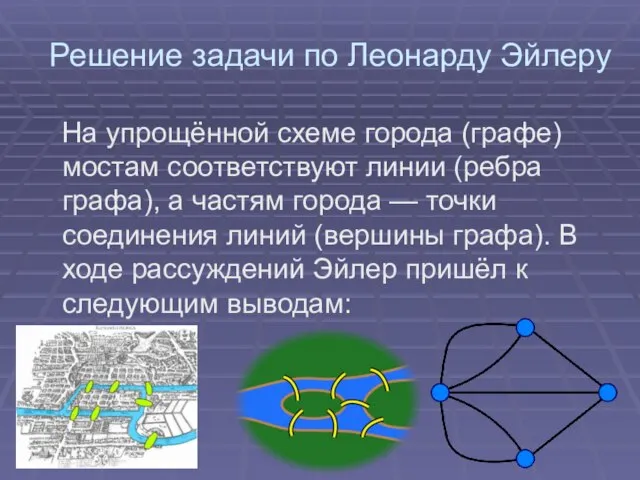
На упрощённой схеме города (графе) мостам соответствуют линии (ребра графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

Решение задачи по Леонарду Эйлеру
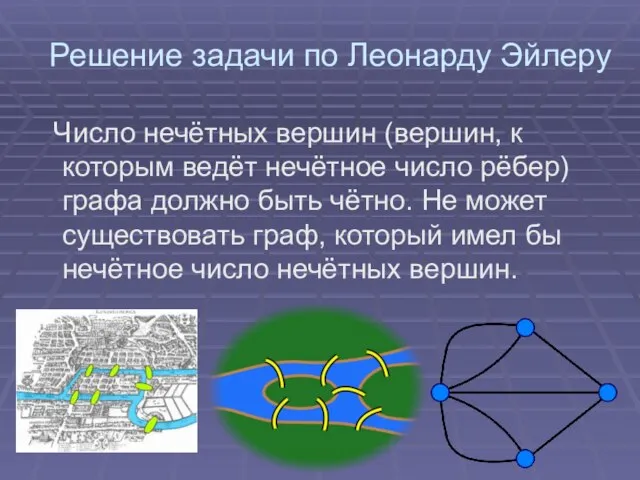
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

Решение задачи по Леонарду Эйлеру
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

Решение задачи по Леонарду Эйлеру
Если ровно две вершины графа нечётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой из нечётных вершин и завершить его в другой нечетной вершине.

Решение задачи по Леонарду Эйлеру
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Решение задачи по Леонарду Эйлеру