Содержание
- 2. Лекция 4
- 3. Операции над событиями
- 4. Пусть дано вероятностное пространство
- 5. СУММА СОБЫТИЙ Суммой А+В двух событий А и В называют событие, состоящее в появлении события А,
- 6. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например,
- 7. Теорема сложения Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р ( А +
- 8. Следствие. Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
- 9. Пример В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного
- 10. Вероятность появления красного шара (событие А) Вероятность появления синего шара (событие В)
- 11. Искомая вероятность : События А и В несовместны.
- 12. Полная группа событий Теорема. Сумма вероятностей событий образующих полную группу несовместных событий, равна единице:
- 13. Пример Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность
- 14. Решение События «пакет получен из города А», «пакет получен из города В», «пакет получен из города
- 15. Следствие. Сумма вероятностей противоположных событий равна единице:
- 16. Пример. В ящике имеется n деталей, из которых m стандартных. Найти вероятность того, что среди k
- 17. Обозначим исходное событие А
- 18. Обозначения
- 19. Вероятность появления хотя бы одного события в n испытаниях Пусть в n независимых испытаниях события появляются
- 20. Теорема. Вероятность появления хотя бы одного из событий независимых в совокупности равна
- 21. Пример Два стрелка стреляют по мишени. Вероятность попадания у первого стрелка p1=0,6; у второго стрелка p2=0,7.
- 22. Решение Зная вероятности попадания стрелков p1=0,6 и p2=0,7, найдем вероятности промаха для каждого стрелка
- 23. Тогда вероятность, что хотя бы один из стрелков попадет
- 24. Произведение событий Произведением (совмещением) двух событий А и В называют событие АВ, состоящее в совместном появлении
- 25. Пример Два стрелка стреляют по мишени. Вероятность попадания у первого стрелка p1=0,6; у второго стрелка p2=0,7.
- 26. Решение Так как вероятность совместного попадания стрелков цель равна произведению вероятностей попадания каждого из стрелков, имеем
- 27. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
- 28. Пример Четыре монеты подбрасывают одновременно. Найти вероятность, что 4 раза выпадет герб.
- 29. Решение Вероятность выпадения герба на одной монете p=1/2 (так как благоприятный исход m=1; общее число исходов
- 30. Условная вероятность
- 31. Условной вероятностью или называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
- 32. Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару,
- 33. Решение. После первого испытания в урне осталось пять шаров, из них три белых. Искомая условная вероятность:
- 34. Условная вероятность
- 35. Теорема умножения вероятностей
- 36. Замечание
- 37. Следствие
- 38. Пример У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем
- 39. Решение. Первый валик- конусный (событие А), второй валик- эллиптический (событие В).
- 41. Пример. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том,
- 42. Решение
- 43. Независимые события. Теорема умножения для независимых событий Событие В называют независимым от события А, если
- 44. Если событие В не зависит от события А, событие А не зависит от события В.
- 45. Для независимых событий теорема умножения
- 46. Пример Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А)
- 47. Замечание. Если события А и В независимы, то независимы также события A и и В, и
- 48. Несколько событий называют попарно независимыми, если каждые два из них независимые.
- 49. Несколько событий называются независимыми в совокупности (или просто независимыми), если независимы каждые два из них и
- 50. Если несколько событий независимы попарно, то отсюда ещё не следует их независимость в совокупности.
- 51. Следствие из Теоремы Умножения. Вероятность совместного появления нескольких событий, независимых в совокупности, равна :
- 52. Задачи
- 53. Найти вероятность совместного появления герба при одном бросании двух монет. Задача 1
- 54. Решение. Вероятность появления герба первой монеты (событие А) Вероятность появления герба второй монеты (событие В)
- 55. Задача 2 Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором –
- 56. Решение. Из первого ящика вынута стандартная деталь (событие А), из второго - В), из третьего –
- 57. События A,B,C независимые, поэтому
- 58. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Задача 3
- 59. Решение. Рассматриваемые события: ={попадание первого орудия}, ={попадание второго орудия}, ={попадание третьего орудия}
- 60. Вероятности событий, противоположных событиям и ( т.е. вероятности промахов), соответственно равны:
- 61. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести
- 62. Решение Приняв во внимание, что, по условию, (следовательно, q = 1 – 0,4 = 0,6)
- 63. получим Учитывая lg0.6
- 64. Вероятность того, что событие появится хотя бы один раз в трёх независимых в совокупности испытаниях, равна
- 65. Решение. Применим формулу P(A) = 0,936; n = 3. р = 1 – q = 1
- 66. Задача 6 Брошены монета и игральная кость. Найти вероятность совмещения событий: появится герб и появится 6
- 67. Решение Вероятность появление герба при броске монеты равна p1=1/2. Вероятность появления 6 очков при броске игральной
- 68. Вероятность совместного появления этих двух событий равна произведению их вероятностей, то есть P(A)=p1·p2=1/2·1/6=1/12
- 69. Задача 7 Вероятность того, что стрелок при одном выстреле попадет в мишень равна p=0,9. Стрелок сделал
- 70. Решение Обозначим события А={первый выстрел попал} B={второй выстрел попал} C={третий выстрел попал} События A,B,C независимые.
- 71. Вероятность, что все три выстрела дали попадание P(ABC) можно найти по формуле умножения для независимых событий
- 72. Задача 8 Вероятность поражения цели первым стрелком p1= 0,7, вторым p2=0,6. Найти вероятность, что цель будет
- 73. Решение Поражение цели только одним стрелком означает, что первый попал и второй не попал или первый
- 74. Подставив значения, имеем P(A)=0,3·0,6+0,7·0,4=0,44
- 75. Задача 9 Среди 100 лотерейных билетов 5 выигрышных. Найдите вероятность того, что 2 наудачу купленных билета
- 76. Решение Обозначим события A={первый билет выигрышный} B={второй билет выигрышный} Вероятность события P(A)=5/100 Вероятность события B, при
- 77. Подставим найденные значения в формулу P(AB)=5/100·4/99=1/495
- 78. Вопросы к лекции 4 Теорема сложения вероятностей Вероятность появления хотя бы одного события в n испытаниях
- 80. Скачать презентацию






































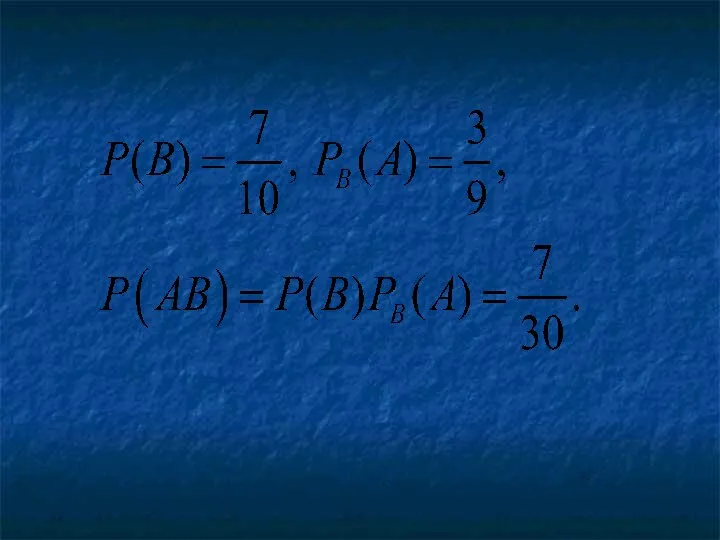






































 Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии Математический дизайн
Математический дизайн Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика
Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений Образец решения уравнения х2=а
Образец решения уравнения х2=а Табличный метод решения задач ЕГЭ по теории вероятностей
Табличный метод решения задач ЕГЭ по теории вероятностей Практикум. Демографические задачи
Практикум. Демографические задачи Приёмы умножения числа 2
Приёмы умножения числа 2 Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные Случайные события
Случайные события Тела вращения
Тела вращения Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Основы матричной алгебры
Основы матричной алгебры элементы теории множеств
элементы теории множеств Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости Презентация на тему Построение треугольника по трем элементам
Презентация на тему Построение треугольника по трем элементам  Производная сложной функции
Производная сложной функции Предмет вычислительной математики. Численные методы
Предмет вычислительной математики. Численные методы Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Треугольник
Треугольник Показательная функция
Показательная функция praktika_3
praktika_3 Задания с фигурами
Задания с фигурами Математика. Проверочная работа
Математика. Проверочная работа Переменные величины и их свойства
Переменные величины и их свойства Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"