Описание свойств функции с помощью графика

Схема исследования функции:
Область определения функции.
Наибольшее, наименьшее значения функции
Непрерывность.
Нули функции.
Промежутки знакопостоянства.
Промежутки возрастания, убывания функции.
Множество значений функции.

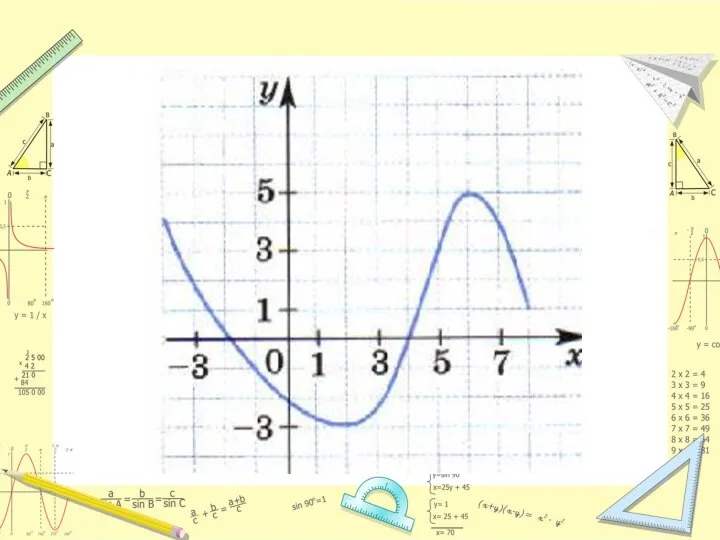
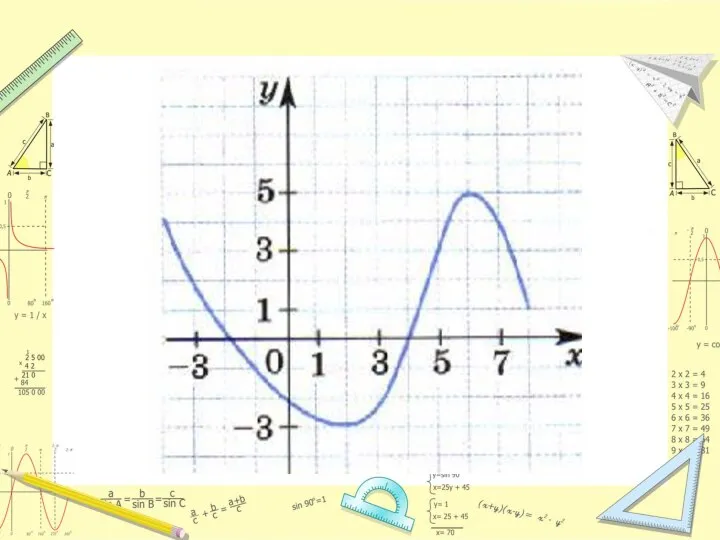
Все значения, которые принимает независимая переменная (аргумент), образуют область определения функции.
D(f)=[ -4; 8]

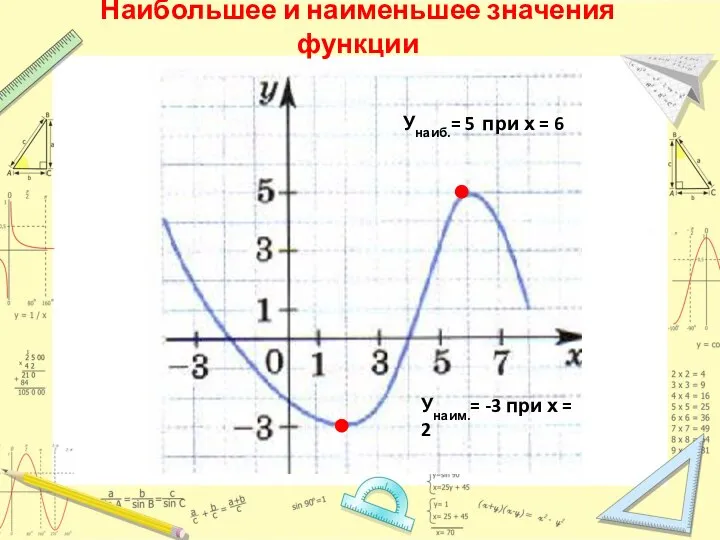
Наибольшее и наименьшее значения функции
Унаим.= -3 при х = 2
Унаиб.= 5 при х = 6

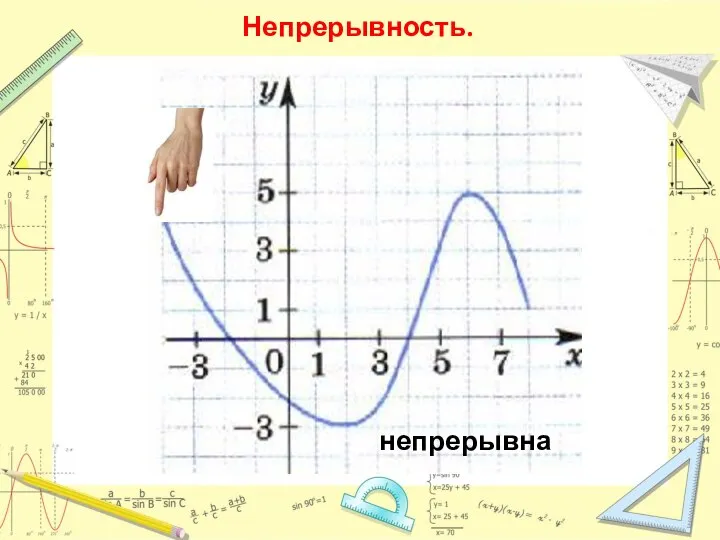
Непрерывность.
непрерывна

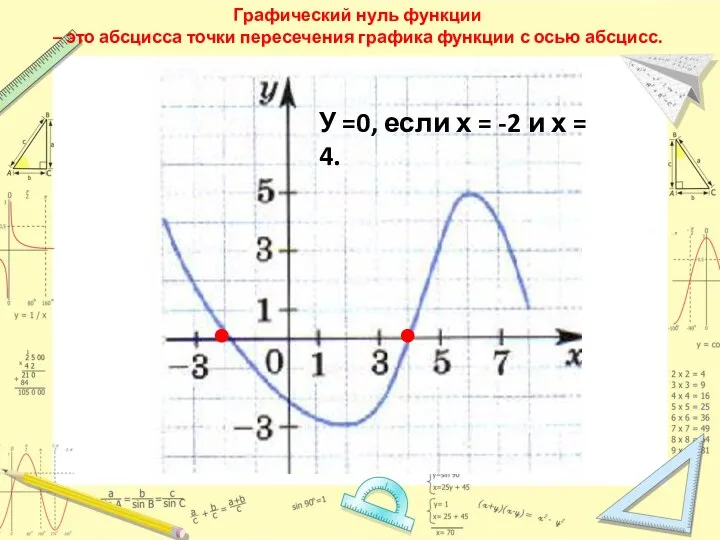
Графический нуль функции
– это абсцисса точки пересечения графика функции с осью абсцисс.
У =0, если х = -2 и х = 4.

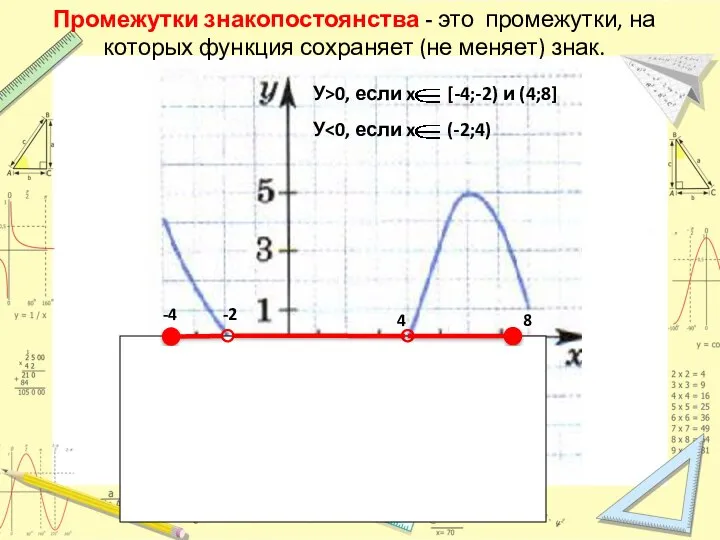
Промежутки знакопостоянства - это промежутки, на которых функция сохраняет (не меняет) знак.
.
-2
-4
8
4
У>0, если x [-4;-2) и (4;8]
У<0, если x (-2;4)

Промежутки возрастания и убывания функции.
Возрастает на отрезке [2;6]
Убывает на отрезке [-4;2] и на отрезке [6;8]

Множество значений функции – все значения зависимой переменной
E(f) = [-3; 5]

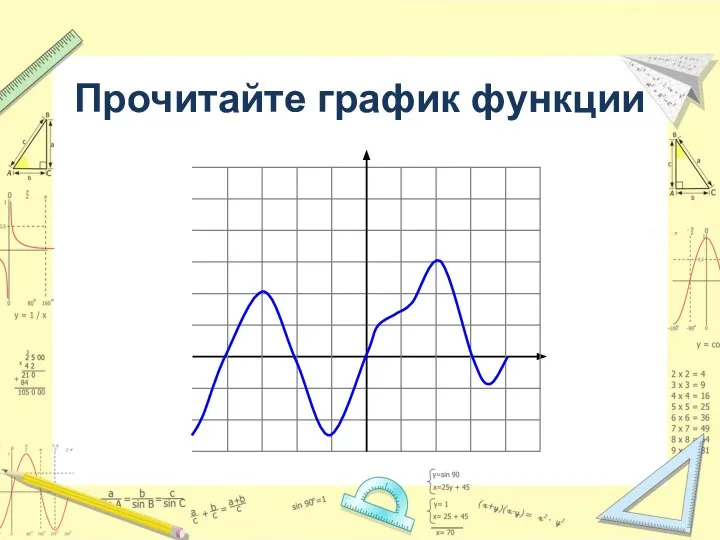
Прочитайте график функции