Предел последовательности. Практическая работа № 24

РЕШИТЕ ПРИМЕР
1
1

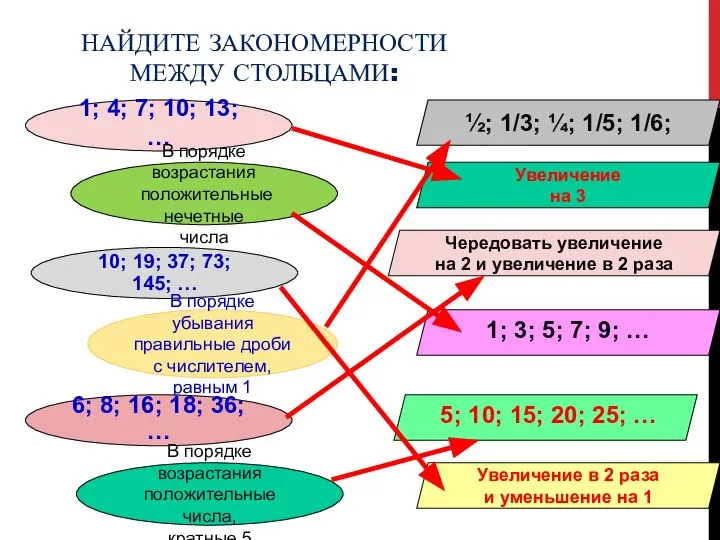
НАЙДИТЕ ЗАКОНОМЕРНОСТИ МЕЖДУ СТОЛБЦАМИ:
1; 4; 7; 10; 13; …
В порядке возрастания положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1

Последовательности заданы формулами:
an=(-1)nn2
an=n4
an=n+4
an=-n-2
an=2n-5
an=3n-1
Впишите пропущенные члены последовательности:
1; ___; 81; ___; 625; … 5; ___; ___; ___; 9; … ___; ___; 3; 11; ___;
-1; 4; ___; ___; -25; … ___; -4 ; ___; ___; -7; …
2; 8; ___; ___; ___; …
16 256 6 7 8 -3 -1 27
-9 16 -3 -5 -6
26 80 242

ОПРЕДЕЛЕНИЕ 1
Пусть а – точка прямой, а r – положительное число. Интервал
(а-r; а+r) называют окрестностью точки а, а число r – радиусом окрестности.
Пример: (5,98; 6,02)
a=6 r=0,2

УКАЖИТЕ ОКРЕСТНОСТЬ ТОЧКИ А РАДИУСА R В ВИДЕ ИНТЕРВАЛА, ЕСЛИ:
а) а = 0
r = 0,1
b) a = -3
r = 0,5
в) а = 2
r = 1
г) а = 0,2
r = 0,3
(-0,1; 0,1)
(-3,5; -2,5)
(1; 3)
(-0,1; 0,5)

ОКРЕСТНОСТЬЮ КАКОЙ ТОЧКИ И КАКОГО РАДИУСА ЯВЛЯЕТСЯ ИНТЕРВАЛ
а = 2 r = 1
а) (1; 3)
б) (-0,2; 0,2)
г) (-7; -5)
в) (2,1; 2,3)
а = 0
r = 0,2
а = 2,2
r = 0,1
а = -6
r = 1

ОПРЕДЕЛЕНИЕ 2
Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.
Пишут и читают:
или

ЧЕМУ РАВЕН ПРЕДЕЛ ДАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ?

СВОЙСТВА
1) Предел суммы равен сумме пределов
2) Предел произведения равен произведению пределов
4) Постоянный множитель можно вынести за знак предела
3) Предел частного равен частному от пределов

РЕФЛЕКСИЯ
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Пример 1
Вывод: если степени числителя и знаменателя равны, то в ответе получаем число, равное отношению коэффициентов наибольших степеней.

РЕФЛЕКСИЯ
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Вычислите пределы

ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Пример 2
Пример 3

ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Вычислите пределы