Описанная окружность

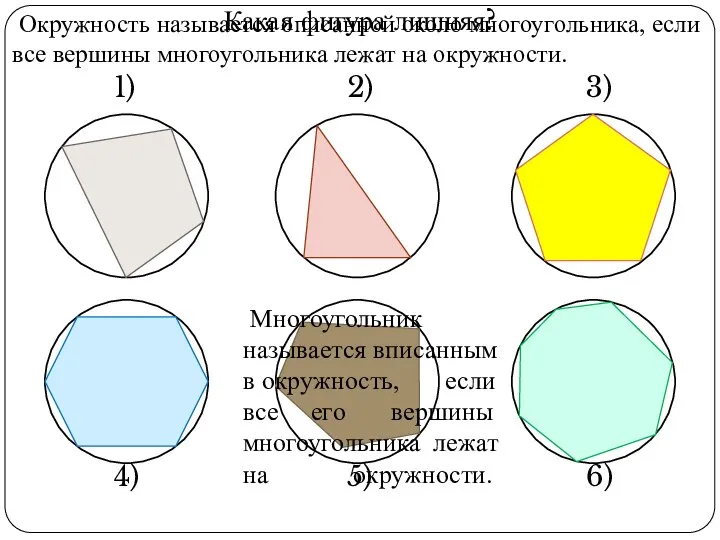
Какая фигура лишняя?
1)
2)
3)
4)
5)
6)
Окружность называется описанной около многоугольника, если
все вершины многоугольника лежат на окружности.
Многоугольник называется вписанным в окружность, если
все его вершины многоугольника лежат на окружности.

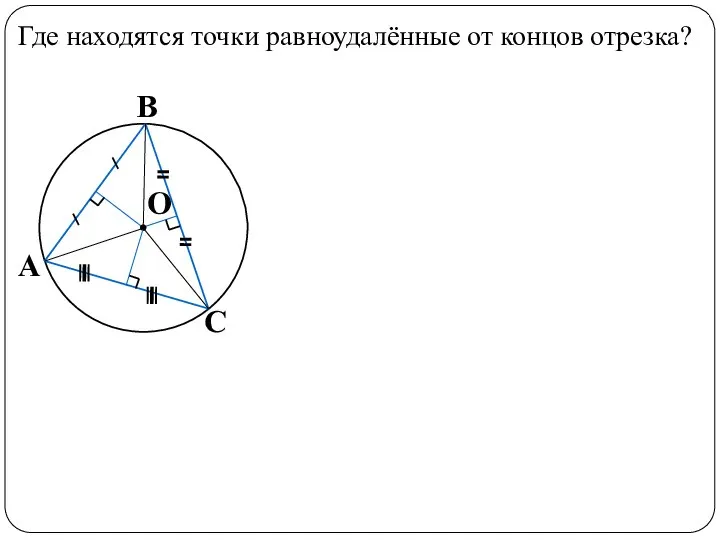
От чего равноудалён центр вписанной окружности?
А
В
С
О
Где находятся точки равноудалённые от концов отрезка?

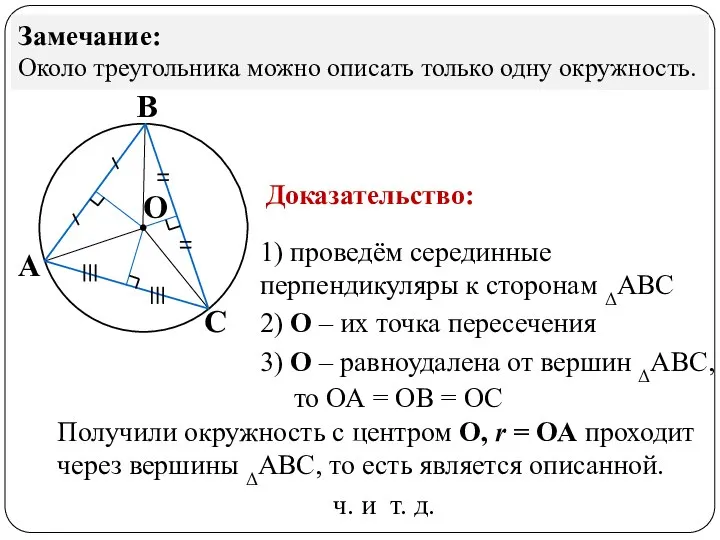
Теорема
Около любого треугольника можно описать окружность.
А
В
С
О
Доказательство:
1) проведём серединные перпендикуляры к сторонам ΔАВС
2) О – их точка пересечения
3) О – равноудалена от вершин ΔАВС,
то ОА = ОВ = ОС
Получили окружность с центром О, r = OA проходит через вершины ΔАВС, то есть является описанной.
ч. и т. д.
Замечание:
Около треугольника можно описать только одну окружность.

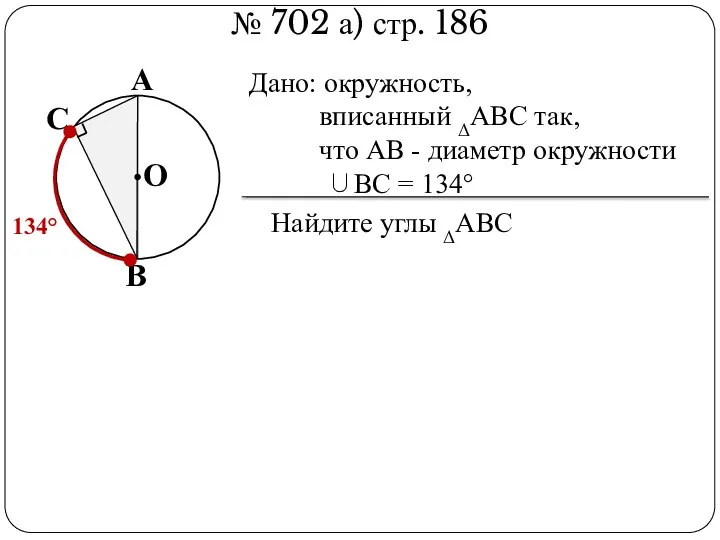
№ 702 а) стр. 186
В
А
С
О
Дано: окружность,
вписанный ΔАВС так,
что АВ - диаметр окружности
∪ВС = 134°
Найдите углы ΔАВС
134°

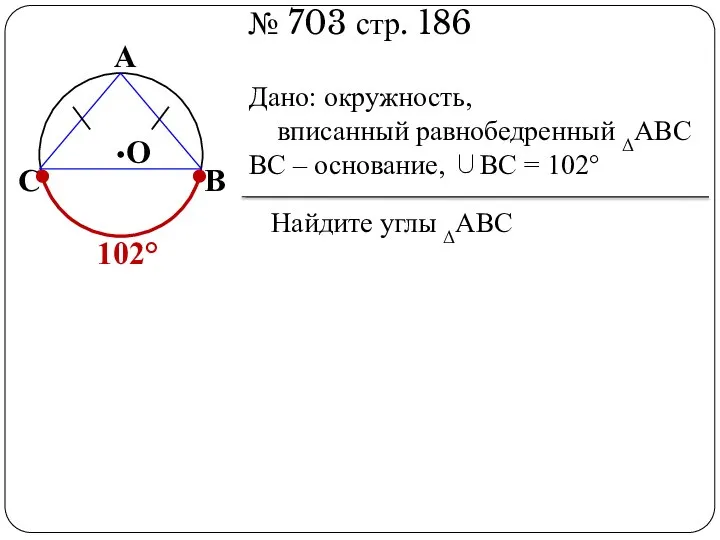
№ 703 стр. 186
В
А
С
О
Дано: окружность,
вписанный равнобедренный ΔАВС
ВС – основание, ∪ВС = 102°
Найдите углы ΔАВС
102°

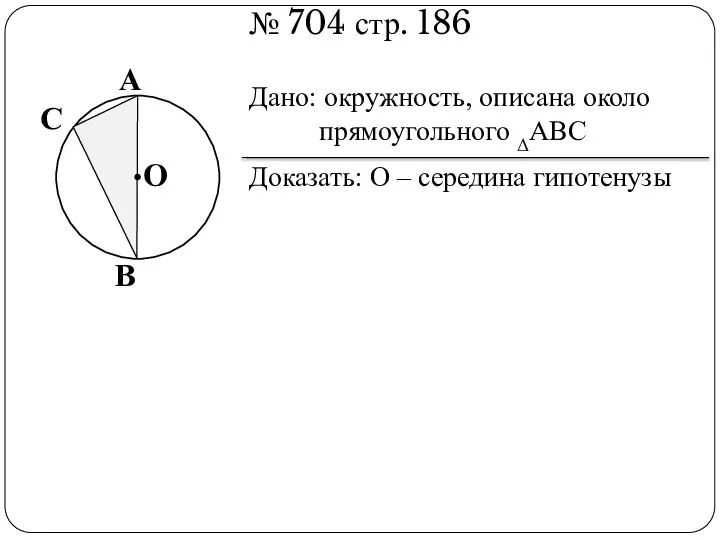
№ 704 стр. 186
Дано: окружность, описана около
прямоугольного ΔАВС
Доказать: О – середина гипотенузы
В
А
С
О