Слайд 2Свойства определенного интеграла
1.

Слайд 3Свойства определенного интеграла
1.
2.

Слайд 4Свойства определенного интеграла
1.
2.
3.

Слайд 5Формула Ньютона-Лейбница
Теорема Пусть y=f(x) – непрерывная на [a,b] функция.
F(x) - любая первообразная
![Формула Ньютона-Лейбница Теорема Пусть y=f(x) – непрерывная на [a,b] функция. F(x) -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893476/slide-4.jpg)
для функции y=f(x). Тогда
Слайд 6Вычисление площадей плоских фигур
1)Пусть y=f(x) – непрерывная и неотрицательная на [a,b]
![Вычисление площадей плоских фигур 1)Пусть y=f(x) – непрерывная и неотрицательная на [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893476/slide-5.jpg)
функция. Тогда площадь фигуры под графиком y=f(x)
на [a,b] равна
Слайд 7Вычисление площадей плоских фигур
2) Пусть y=f(x) – непрерывная и неположительная на [a,b]
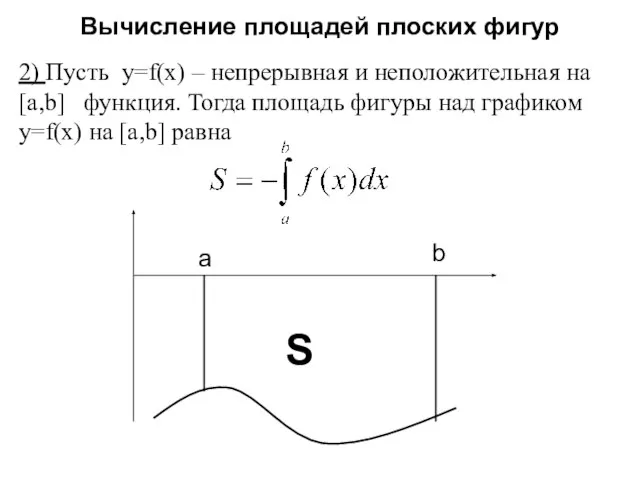
функция. Тогда площадь фигуры над графиком y=f(x) на [a,b] равна



![Формула Ньютона-Лейбница Теорема Пусть y=f(x) – непрерывная на [a,b] функция. F(x) -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893476/slide-4.jpg)
![Вычисление площадей плоских фигур 1)Пусть y=f(x) – непрерывная и неотрицательная на [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893476/slide-5.jpg)

 Урок повторения и самоконтроля
Урок повторения и самоконтроля Презентация на тему Движение. Виды движения
Презентация на тему Движение. Виды движения  Пространственные и временные представления
Пространственные и временные представления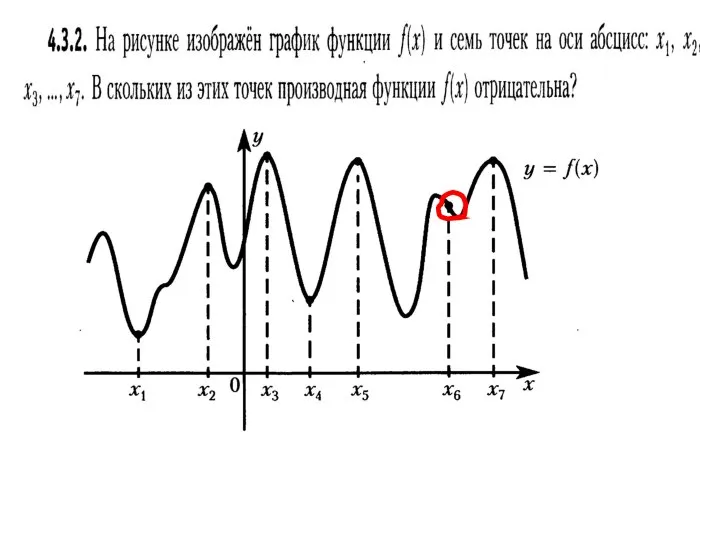 Графики функций
Графики функций Статистическая радиотехника. Случайный процесс, ансамбль его реализаций
Статистическая радиотехника. Случайный процесс, ансамбль его реализаций Координаты на прямой
Координаты на прямой Интегрирование тригонометрических и иррациональных функций
Интегрирование тригонометрических и иррациональных функций Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Понятие многогранника, призмы и их элементов
Понятие многогранника, призмы и их элементов Численные решения обыкновенных дифференциальных уравнений (ОДУ)
Численные решения обыкновенных дифференциальных уравнений (ОДУ) Графики функций. Устная работа
Графики функций. Устная работа Задачи на сложение и вычитание
Задачи на сложение и вычитание Презентация на тему Квадратное уравнение и его корни
Презентация на тему Квадратное уравнение и его корни  Случаи вычитания 11-
Случаи вычитания 11- Метр. (2класс)
Метр. (2класс) Эконометрика. Лекция 2
Эконометрика. Лекция 2 Провешивание прямой на местности
Провешивание прямой на местности Обыкновенные дроби
Обыкновенные дроби Теорема косинусов
Теорема косинусов Площадь параллелограмма
Площадь параллелограмма Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Презентация на тему Арифметика Магницкого
Презентация на тему Арифметика Магницкого  Цилиндр. Цилиндры вокруг нас
Цилиндр. Цилиндры вокруг нас Кредиты в нашей жизни или элементы финансовой математики
Кредиты в нашей жизни или элементы финансовой математики Построение графика квадратичной функции
Построение графика квадратичной функции Многоугольники. Виды многоугольников
Многоугольники. Виды многоугольников Деление окружности на 5 равных частей. Сопряжение
Деление окружности на 5 равных частей. Сопряжение Логарифм числа и его свойства
Логарифм числа и его свойства